極值點偏移問題的解法探究
——從對數(shù)平均不等式談起

梁昱韜

(江蘇省蘇州中學(xué)高二(17)班，215007)

高中導(dǎo)數(shù)題中有這么一類題,它們既復(fù)雜多變,又有規(guī)可循;既形式花哨,又本質(zhì)歸一,這便是極值點偏移問題.此類問題的解決方法多樣,本文從對數(shù)平均不等式談起,由淺入深地討論此類問題的一類解法.

一、千呼萬喚始出來,猶抱琵琶半遮面

結(jié)論對任意兩個不同正實數(shù)a,b,恒有不等關(guān)系(對數(shù)平均不等式)

①

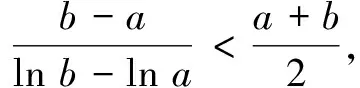
二、紙上得來終覺淺,絕知此事要躬行

我們首先通過一道例題求解,感受應(yīng)用對數(shù)平均不等式解決極值點偏移問題的過程與功效.

例1已知函數(shù)f(x)=ex-ax(a≠0).

(1)討論f(x)零點的個數(shù);

(2)若f(x)有兩個零點x1,x2，且x12.

解(1)當(dāng)a∈(-∞,0)∪{e}時,f(x)有唯一零點;當(dāng)a∈(0,e)時,f(x)無零點;當(dāng)a∈(e,+∞)時，f(x)有兩個零點.(過程略)

(2)解法1常規(guī)解法

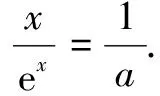
解法2對數(shù)平均不等式法

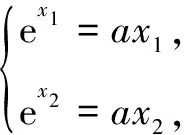
反思比較可見對數(shù)平均不等式帶來的證明更為簡潔、對稱、美觀. 看似保留雙變量，實則通過齊次性隱匿了單變量的身份，這便是該解法的精髓所在.值得一提的是，在高考中對數(shù)平均不等式需要證明，此處不再贅述.

三、不識廬山真面目,只緣身在此山中

必須承認(rèn),直接應(yīng)用對數(shù)平均不等式遠(yuǎn)不能解決所有雙變量對稱齊次形式的問題.因此，需要我們將對數(shù)平均不等式進(jìn)行變式推廣.

例2已知函數(shù)f(x)=ex-ax2-ax.

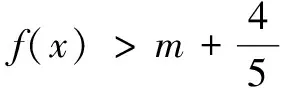
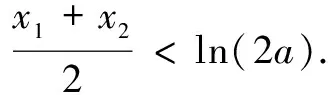
解(1)略.

(2)f′(x)=ex-2ax-a，由f′(x1)=f′(x2)=0，得

②

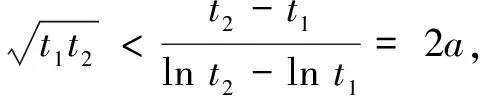
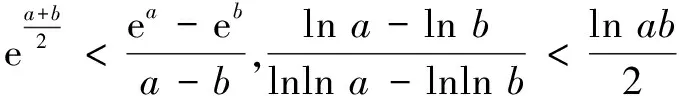
四、山重水復(fù)疑無路,柳暗花明又一村

在處理完雙變量齊次對稱式后，我們不禁疑惑，對于雙變量非對稱齊次式又該如何解決呢?事實上，縱使對數(shù)平均不等式在此處已無用武之地，但其相除、相減的思想是深刻而普遍……