提高初中學生探究數(shù)學例題的能力

彭雨清

【摘要】“發(fā)展能力”是數(shù)學的主要目標與核心內(nèi)容，它是初中生提高數(shù)學素養(yǎng)的關鍵，是學生在從事“數(shù)學思考”過程中，在“發(fā)現(xiàn)問題”“提出問題”“分析問題和解決問題”等能力方面的發(fā)展。

【關鍵詞】提高能力;初中生;數(shù)學例題;探索與思考

數(shù)學課程總目標指出，學生能體會數(shù)學知識之間、數(shù)學與其他學科之間、數(shù)學與生活之間的聯(lián)系，運用數(shù)學的思維方式和解決問題的能力。這個目標體現(xiàn)了對學生在掌握數(shù)學和通過學習數(shù)學而達到的自身發(fā)展方面的要求：發(fā)展能力。例題教學是數(shù)學課堂教學的一個重要環(huán)節(jié)， 但是有的教師認為教材中的例題太簡單，往往不講或是一帶而過，或照本宣科，沒讓學生真正理解題目所蘊含的數(shù)學知識及思想方法， 沒有讓學生經(jīng)歷知識的發(fā)生發(fā)展過程，而只是就題講題，就知識點講知識點，使學生的例題學習總停留在表層，一知半解，模仿式學習，甚至死記硬背，結(jié)果例題講解完后一做練習，學生仍不會解題。 對于例題的教學，我是從如下四個方面跟學生一起探討的：

一、預習中發(fā)現(xiàn)問題

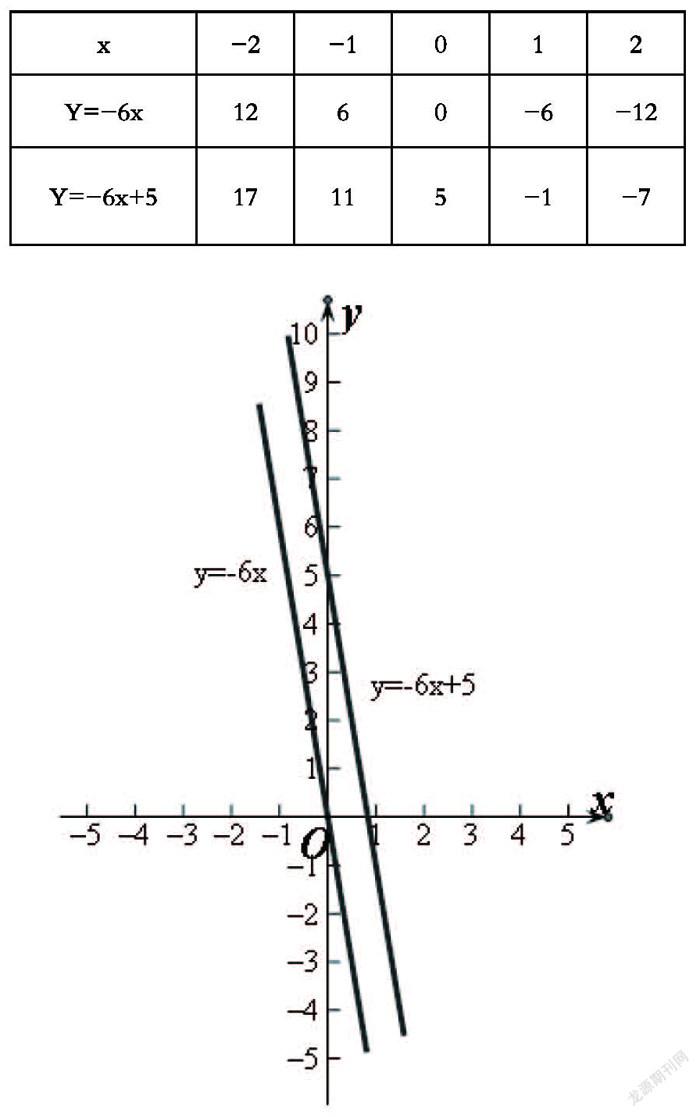
“發(fā)現(xiàn)問題”是指面對一些表面上看起來沒有確定的疑問或矛盾的現(xiàn)象時，從數(shù)學的角度思考、尋找其中可能存在的數(shù)量或者空間方面的某些聯(lián)系，進而發(fā)現(xiàn)隱含的數(shù)學方面的疑問或矛盾，并由此提煉出確定的問題。教材中的例題是數(shù)學專家精心設計或精挑細選的有價值的知識， 同時課本例題解答有較強的示范作用。 例題的解答既是學生今后書寫習題解答的方法來源， 也是學生今后書寫習題解答過程的示范和標準。因此， 我們應該重視對課本例題的研究。在教學中， 教師首先要注意引導學生對例題的思考。先看看學生上課前的預習： 例：人教版八年級數(shù)學下冊91頁例2畫出函數(shù)y=-6x與y=-6x+5的圖象。

解：列表：

描點并連線：

學生在預習上面例題時存在以下疑問：

學生甲：不是學一次函數(shù)的圖象嗎，為什么還畫正比例函數(shù)的圖象？

學生乙：列表時不是一個函數(shù)一個函數(shù)的列嗎？列在一起看不明白？

學生丙：一次函數(shù)的圖象是一條直線，不是找兩點更簡單嗎？

學生丁：一次函數(shù)的圖象跟正比例函數(shù)的圖象是一樣的嗎？

二、課堂上提出問題

“提出問題”是指在已經(jīng)發(fā)現(xiàn)問題的基礎上，把發(fā)現(xiàn)的疑問或矛盾用數(shù)學語言、數(shù)學符號集中地以“問題”的形式表述出來——包括已知條件、限定因素、需求目標等。教學時以課本的例題為根本， 盡可能在原例題基礎上讓學生嘗試著根據(jù)題目的已知、求知、圖象等等，激發(fā)學生創(chuàng)新的熱情，促使學生思維發(fā)散，提出問題，開拓解題思路，從而幫助學生克服思維狹窄性和思維定勢，有利于學生核心素養(yǎng)的提升。如上題：

學生1：畫y=-6x+5的圖象找兩點（0，5）和（1，-1）直接畫是不是更簡單？

學生2：y=-6x

y=-6x+5

然后再描點連線，這樣是不是更清晰些？

學生3：y=-6x的圖象經(jīng)過原點，函數(shù)y=-6x+5的圖象會經(jīng)過哪些特殊的點？

學生4：函數(shù)y=-6x+5的圖象可以由y=-6x的圖象平移得到，那么函數(shù)y=-6x+5的性質(zhì)是不是跟y=-6x的性質(zhì)是一樣的？

三 、通過例題分析問題

教師在課堂上啟發(fā)、引導學生從不同的角度、不同的思路，用不同的方法和不同的角度去分析一道數(shù)學例題，一可以充分調(diào)動學生思維的積極性， 提高他們綜合運用已學知識解答數(shù)學問題的技能技巧;二是為了鍛煉學生思維的靈活性，促進他們長知識、長智慧;三是為了開闊學生的思路，引導學生靈活地掌握知識的縱橫聯(lián)系，培養(yǎng)和發(fā)揮學生的創(chuàng)造性。

老師：你們在課堂上能積極提出不同的問題，老師很高興，說明你們認真地去預習了，而且你們的數(shù)學思維已經(jīng)具有了一定的邏輯性，問題也提得很有質(zhì)量、有代表性、有挑戰(zhàn)性，希望你們繼續(xù)努力。下面我們一起來解析這個例題：

前幾節(jié)課學習了畫函數(shù)圖象三步法：列表、描點、連線，又從定義、圖象、性質(zhì)、應用四方面探討了正比例函數(shù)。那么這節(jié)課從畫y=-6x+5圖象的基礎上來探討一次函數(shù)y=kx+b（k0）的性質(zhì)和應用。大家通過畫一次函數(shù)y=-6x+5的圖象，來分析y=kx+b（k0）的圖象可以怎樣畫？從圖象中可以得到哪些信息？

學生1：畫y=-6x+5的圖象可以用平移法：先畫y=-6x再把它往上平移5個單位得到y(tǒng)=-6x+5的圖象。

學生2：我是用兩點法畫y=-6x+5的圖象，A（0，5）和B（1，-1）兩點，因為預習后已經(jīng)知道一次函數(shù)的圖象是一條直線，又因為兩點確定一條直線，所以兩點法更好用。

學生3：那么畫一次函數(shù)y=kx+b的圖象有兩種方法：

（1）平移法：先畫y=kx的圖象，然后上下平移|b|，

當b>0時向上平移|b|;當b<0時向下平移|b|。

（2）兩點法：找A（0，b）和B（1，k+b）.

學生4：找兩點時，找數(shù)軸上的兩點更準確：在y軸上的A（0，b），在x軸上的點。找這兩點還方便求y=kx+b與兩坐標軸圍成的三角形的面積。

學生6：還有y=-6x和y=-6x+5的形狀是相同的，而且從左往右看都是走下坡路，y隨x的增大而減少，傾斜程度相同，都經(jīng)過二、四象限，只是y=-6x+5還經(jīng)過第一象限。

學生7：發(fā)現(xiàn)當k相等時，y=-6x和y=-6x+5兩個函數(shù)的圖象是平行的，后面那個例題中的b相等時兩圖象是相交的，并且交點在y軸的（0，b）處。

老師：沒想到通過一個例題的學習，同學們的思維這么活躍，通過分析例題能總結(jié)出這么多性質(zhì)和應用規(guī)律，希望你們以后繼續(xù)保持這種積極思考、積極提問、積極回答的好習慣。

四、根據(jù)例題解決問題FFD8CF48-A6E6-487D-A93D-2ECDA63C8807

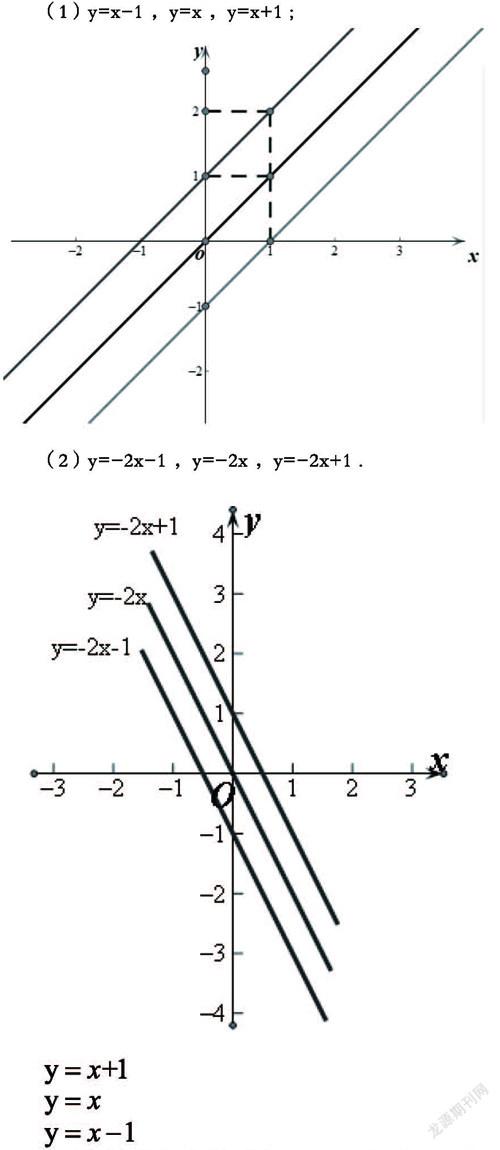
學生的數(shù)學能力主要是通過邏輯思維來提高的，怎樣來培養(yǎng)學生數(shù)學邏輯思維能力，主要通過從做題、講解、探索、思考、運用、總結(jié)中得來。培養(yǎng)學生的邏輯思維能力是培育初中生數(shù)學能力最基本的目標。目的是為了初中生能夠靈活掌握初中數(shù)學知識，而不僅僅是機械地學習數(shù)學知識，在現(xiàn)實實踐中能夠靈活運用，舉一反三，達到所培養(yǎng)的學生具有更強競爭力的根本目的。目前，在新時期新課標規(guī)則中，明確規(guī)定學校不能只從考試成績一個衡量標準來反應學生的真實發(fā)展狀況，不允許所培養(yǎng)的學生只為了應對考試而進行機械的學習，而不知其內(nèi)涵。應把創(chuàng)新教學思路和教學方式并行提到首要地位，協(xié)調(diào)學生的創(chuàng)新性思維和學習能力共同發(fā)展，使學生的數(shù)學學習能力與方法得到提高。如：學生對上個例題有了深入的探索、思考后，已經(jīng)理解了，所以對于類似的題就迎刃而解了。練習：在同一直角坐標系中畫出下列函數(shù)的圖象，并指出每小題中三個函數(shù)的圖象有什么關系？

（1）y=x-1 ，y=x ，y=x+1 ;

（2）y=-2x-1 ，y=-2x ，y=-2x+1 .

今天的作業(yè)是把這節(jié)課的例題和練習整理好，并把k>0和k<0時一次函數(shù)y=kx+b的性質(zhì)、應用的筆記整理好。

五、結(jié)束語

總之，在課堂中要有疑問、沉思、聯(lián)想，讓問題和方法貫穿學習始終，讓解決問題成為一種習慣、一種能力，這樣才能培養(yǎng)學生的思維能力。而且教科書例題具有示范引領、鞏固新知、展示新知、思維訓練、揭示方法、文化育人等功能，學生獲得數(shù)學概念、掌握數(shù)學定理、發(fā)展數(shù)學能力都離不開例題。因此，對教科書例題的研究十分必要且有意義。

參考文獻：

[1]馬復.初中數(shù)學新版課程標準解析與教學指導[M].北京：北京師范大學出版社，2012.

[2]邢夢林.初中數(shù)學例題的教學策略初探[J].安國市教育局教研室，2018.

[3]王曉麗，張明亮.中美初中數(shù)學教科書有理數(shù)例題的比較研究[J].數(shù)學與統(tǒng)計學院，2018.

[4]王凱旋.課本例題解答的建議與另解[J].湖北省武漢市華中科技大學同濟附中，2018.

[5]戴德文.學以致用 ——初中數(shù)學教學中注重培養(yǎng)學生解題思路的研究[J].重慶市大足區(qū)城西中學，2019，5.FFD8CF48-A6E6-487D-A93D-2ECDA63C8807