一道立幾試題的解法賞析及變式拓展

劉海濤

(安徽省蕪湖市第一中學，241000)

一、試題呈現

題目如圖1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2BC=2CD=2,P為四邊形ABCD所在平面外一動點,且PA=PB,∠APB=90°,設M為PD的中點,則CM的值為______.

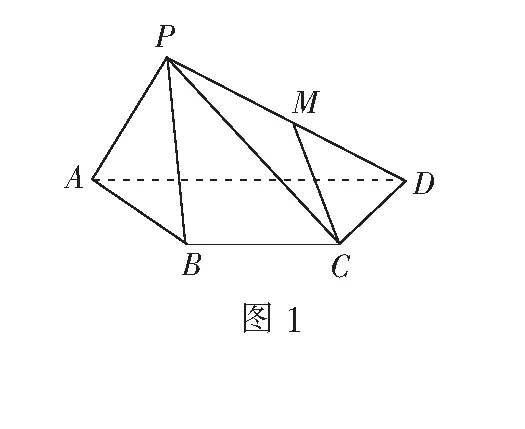
這是筆者所在學校高三的一道模考題,試題結構簡單明了,形式上為求線段的長度問題,主要考查空間線面的平行與垂直關系、解三角形等知識,體現了邏輯推理、直觀想象、數學運算等核心素養的綜合考查.筆者發現該題內涵豐富,題中并未說明平面PAB與平面ABCD所夾角的大小,點P為空間中一動點,于是點M亦為動點,但為何線段CM長度卻為定值呢?現將對該題的剖析與讀者分享交流.

二、解法探究

分析1要說明CM的長度為定值,因為不知二面角P-AB-D的大小,所以無法得到線段PC,PD的長度,難以在?PCD中直接解得線段CM長度.而由條件可確定等腰Rt?PAB各邊的長度,故考慮利用平行關系轉化到?PAB中求解.

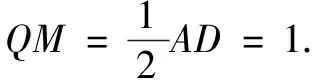
評注本題的解題策略是將動直線CM放入一個相對確定的平面?PAB內,達到“以靜制動”的解題效果.

分析2基于解法1,注意到線段MN為?PAD中對應邊PA的中位線,容易判斷知?MNC的具體形狀,由余弦定理即可求出線段CM的長度.

評注解法2實為解法1的優化,將長度為定值的線段CM構造為一確定三角形的一條邊,直觀展示出線段CM的長度不受二面角P-AB-D大小的影響.實際上,立體幾何中有很多這樣的例子,比如將矩形ABCD沿著其一條對角線AC翻折,無論翻折成多大的二面角B-AC-D,所構成的三棱錐D-ABC的外接球球心始終為線段AC中點,球的半徑始終為線段AC長的一半.

分析3利用空間向量解決……