一道高考壓軸題的探究歷程與教學建議

劉再平 張 琪

(陜西省漢中中學,723000)

一、試題呈現

如圖1，已知拋物線C:x2=2py(p>0)的焦點為F,且F與圓M:x2+(y+4)2=1上點的距離的最小值為4.

(1)求p;

(2)若點P在圓M上,PA,PB是C的兩條切線,A,B是切點,求?PAB面積的最大值.

此道是2021年全國乙卷理科圓錐曲線壓軸題第21題,試題表述簡潔,問題設置循序漸進,有一定的梯度. 第(1)問比較基礎,考查圓外一點到圓上距離的最小值,根據圓的幾何性質即可求出p的值;第(2)問顯然需要用參數表示出?PAB的面積,最后再求面積的最值,是此道壓軸題真正的壓軸點.

二、解法探究

求最值可以從函數、均值不等式和三角函數三個常見的視角出發,梳理解題活動的思維導圖如圖2,從而獲得下列通性通法.

由點P在切線上,得x1x0-2y1-2y0=0,且x2x0-2y2-2y0=0,則點A,B的坐標滿足方x0x-2y-2y0=0,即直線AB的方程為x0x-2y-2y0=0.

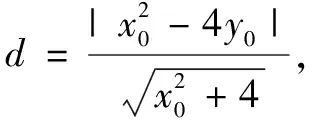
解法2設點P(cosα,-4+sinα),切線方程為y=k(x-cosα)-4+sinα,與x2=4y聯立,可得

x2-4kx-4sinα+4kcosα+16=0.

令Δ=0,得k2-kcosα+sinα-4=0.故切線PA,PB的斜率k1,k2滿足k1+k2=cosα,k1k2=sinα-4,即點P(k1+k2,k1k2).

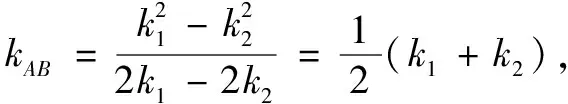
評注解法1通過設點的坐標將三角形面積表示出來,使問題轉化為二次函數的最值問題;解法2利用參數方程將三角形的面積轉化為三角函數最值問題,其中還是需要借助二次函數的性質解題.因此,上述兩種方法都屬于解決此類問題的通法.

三、本質探究

在上述壓軸題中,?PAB稱為阿基米德三角形.阿基米德(公元前287年——公元前212年),古希臘偉大的哲學家、物理學家,并享有“數學之神”的稱號.為了紀念他，將拋物線的弦與過弦的端點的兩條切線所圍成的三角形稱為阿基米德三角形.

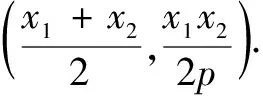
性質2直線AB的方程為(x1+x2)x-2py+x1x2=0.

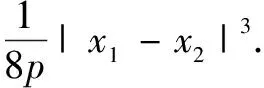
性質4直線AB過拋物線內一定點C(xc,yc)時,點P的軌跡方程為xcx-py-pyc=0.特別地……