四個(gè)結(jié)論“玩轉(zhuǎn)”分組分配問題

陳雪梅

(甘肅省清水縣第六中學(xué),741400)

排列組合教學(xué)中的不同元素與相同元素的分組問題是高中數(shù)學(xué)的一個(gè)難點(diǎn),很多同學(xué)在解決這類問題時(shí)要么束手無策,要么一做就錯(cuò).本文將通過一些具體的例子,介紹如何利用四個(gè)相關(guān)結(jié)論解決這類問題.

一、不同元素的分組問題

例1將a,b,c,d四個(gè)不同的小球平均分成兩組,有多少種不同的分法?

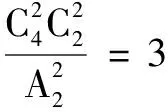
變式1將a,b,c,d四個(gè)不同的小球分成三組,其中一組兩個(gè)小球,其余兩組各一個(gè)小球,有多少種不同的分法?

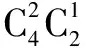
變式2將a,b,c,d四個(gè)不同的小球分成兩組,其中一組1個(gè)小球,另一組3個(gè)小球,有多少種不同的分法?

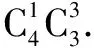
通過以上例題與變式,我們不難概括得到如下結(jié)論:

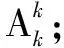
變式3將a,b,c,d四個(gè)不同的小球裝在甲、乙兩個(gè)不同的盒子中,求在下列條件下各有多少種不同的分配方法?

(1)每盒各兩球;

(2)一盒一球,一盒三球.

分析求解這類問題可以分兩個(gè)步驟:先分組后分配.

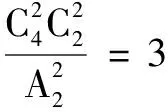
結(jié)論2一般地,如果把不同的元素分配給幾個(gè)不同對(duì)象,采用的方法是先分組后分配,則不同分法為分組方案數(shù)乘以不同對(duì)象數(shù)的全排列數(shù).

以上是我們以不同的小球分組問題為例總結(jié)的解題方法,同學(xué)們可以以此為模板解決所有不同元素的分組分配問題.

高考鏈接

1.(2020年全國高考題)4名同學(xué)到3個(gè)小區(qū)參加垃圾分類宣傳活動(dòng),每位同學(xué)只去1個(gè)小區(qū),每個(gè)小區(qū)至少安排1位同學(xué),不同的安排方法有______種.

分析此題為不同元素的分組分配問題.4名同學(xué)分3組,其中一組兩位同學(xué),另外兩組……