增量代換法求解零點不等式問題
2022-05-09 02:33:00王國軍吳瑞環
高中數學教與學
2022年7期
王國軍 吳瑞環
(河北省石家莊市第二中學,050000)
導數是研究函數性質的核心工具,在研究函數性質的過程中,零點是最為核心和關鍵的問題.近幾年,零點問題是高考和模擬考試的熱點問題,一類涉及函數零點的不等式備受命題人青睞,成為理所當然的把關壓軸題.學生對于這類問題并不陌生,也知道需要消元轉化為一元函數不等式求解.但如何才能將不能顯性表示的零點表示出來,成為壓倒駱駝的最后一根稻草.本文挑選幾例模擬試題,給出增量代換法表示零點的可操作性過程,供大家高三復習備考.
一、增量法解決零點問題的過程
先用一道高考真題,給出增量代換法解決問題的具體過程.
例1(2010天津高考題)設函數f(x)=xe-x,x∈R.若f(x1)=f(x2),且x1≠x2,求證:x1+x2>2.
分析由已知條件得到一個方程,且含有超越結構,此時x1,x2無法具體表示出來;為表示出x1,x2,需要借助x1,x2之間的新的運算關系,構造方程組求解.
解不妨設x1 第一步:引入參數t作為增量. 第二步:用增量表示零點x1,x2. 第三步:將多元不等式轉化為關于增量的一元函數不等式. 第四步:證明一元函數不等式,使問題獲解. 所以g(t)>2,即x1+x2>2.得證. 1.利用零點之比,引入增量參數 例2已知函數f(x)=lnx-ax+1(a∈R). (1)討論函數f(x)的單調性; 分析第(1)問需對參數進行簡單的分類討論;第(2)問要能想到對目標不等式取自然對數進行轉化,再利用增量代換法處理. 解(1)當a≤0時,易見函數f(x)在(0,+∞)單調增. 例3已知函數f(x)=lnx-ax+2(a∈R)有兩個零點x1,x2. (1)求實數的取值范圍; 解(1)(0,e).(過程略) 綜上,得證. 2……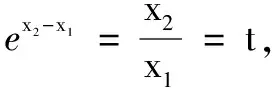
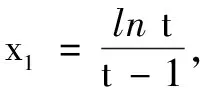
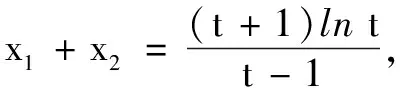
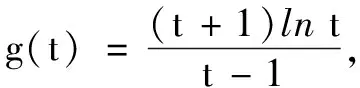
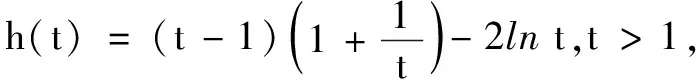

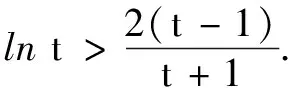
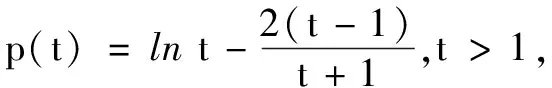
二、增量引入的常見方法

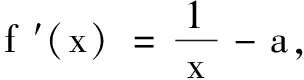
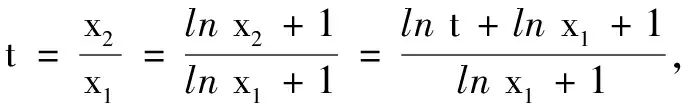
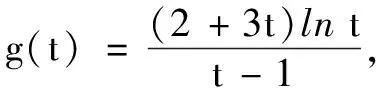
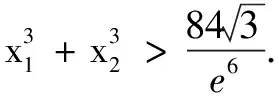
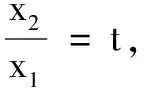
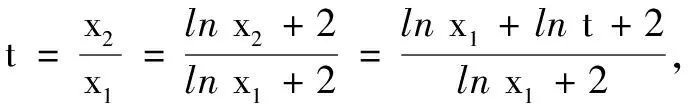

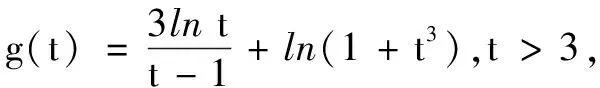
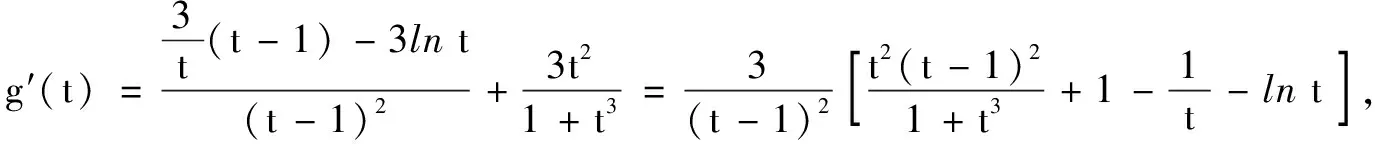
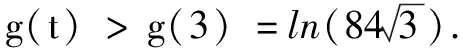 登錄APP查看全文
登錄APP查看全文
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
作文世界(小學版)(2018年4期)2018-10-16 17:13:34
快樂作文·低年級(2016年12期)2017-01-03 20:52:44
快樂作文·低年級(2016年6期)2016-06-24 18:58:40
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
中學生數理化·高二版(2008年7期)2008-06-15 01:31:20

