立足問題情境 凸顯核心素養
——從幾何求值問題談起

王玉宏

(江蘇省揚州市教育科學研究院, 225000)

《普通高中數學課程標準(2017年版2020年修訂)》明確指出:數學在形成人的理性思維、科學精神和促進個人智力發展的過程中發揮著不可替代的作用,并凝練提出六個數學核心素養,包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析[1].幾何求值問題以幾何圖形為情境,融幾何、代數與關系為一體,很好地體現了現代數學的本質,能夠突出數學學科核心素養.

在數學教學中,考試評價的導向作用是明顯的,引領一線的數學教學.本文以幾道幾何求值試題為例,分析其如何指向核心素養考查及其教學啟示,以期發揮考試評價的導向作用,對深化課程改革、落實核心素養發揮作用.

一、劍指核心素養的幾何求值問題梳理

幾何求值問題大致可分為幾何定值問題和幾何最值問題.

1. 幾何定值問題

(1)靈活運用方程模型，解決幾何求值問題

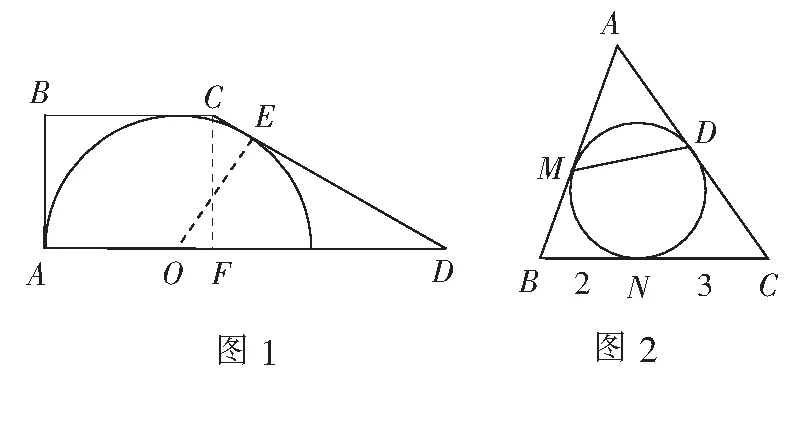
例1如圖1,圓心O在直角梯形ABCD的大底上,半圓與AB,BC,CD相切,已知∠ADC=30°,圓的半徑為R,求梯形的面積S.

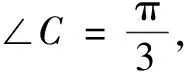
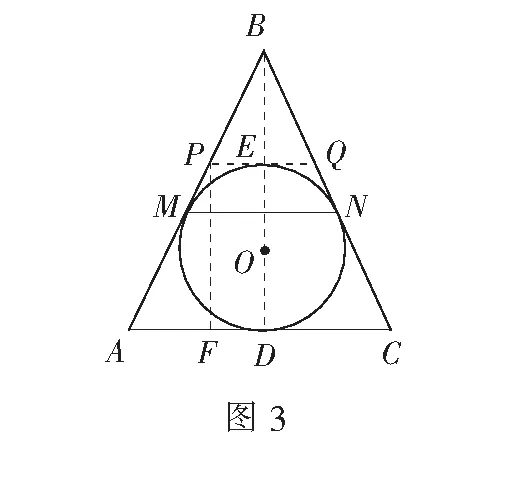
例3如圖3,已知?ABC的內切圓半徑為3,且AB=BC,頂點B到圓心O的距離為6,內切圓與腰AB,BC的切點分別為M,N.求MN的長.

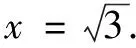
試題評析以上三例均以圓和三角形、四邊形的邊相切為背景,線段的和差關系、余弦定理、勾股定理、相似三角形是探索求解問題思路的思維基礎，布列方程實現了形向數的轉化,考查學生自覺應用方程模型解決邊長求值問題的意識和能力,發展了學生的直觀想象素養.

(2)綜合運用推理計……