基于流固耦合的水翼渦振特性分析

2022-05-09 02:42:28劉新月馬如相杜雷雨

兵器裝備工程學報 2022年4期

劉新月，洪亮，馬如相，南栩，杜雷雨

(南京理工大學能源與動力工程學院，南京 210094)

1 引言

近年來，隨著船舶行業的蓬勃發展，艦艇的航速大大提升，艦艇水下結構的水彈性振動得到了造船界的重視。若艦艇的航速大，舵翼的結構強度不高，舵翼在水下運動時有可能會產生顫振，造成結構破壞，威脅航行安全。而在艦艇航速較低時，會產生一種容易被忽視的振動現象“渦振”，渦振即結構在流場中產生渦的頻率與結構固有頻率一致時發生的共振現象。渦振雖然是限幅運動，但會造成結構疲勞，長此以往，造成結構破壞。對于潛艇來說，發生渦振時會產生顯著的噪聲，破壞隱身性能。

針對水翼的振動現象，國內外的眾多學者展開了研究。Chen等[1]采用SSTk-ω湍流模型對平行槽水翼葉片進行數值分析，研究了水翼位置和間距對渦產生的抑制效果和流動特性的影響。結果表明，葉片間距越小，越容易產生渦，并根據分析結果選取翼型。Huang等[2]選用NACA0012翼型進行了試驗，著重探究了翼梢對渦激振動的影響，發現翼梢處容易產生渦量大的渦。Huerre等[3]以及Oertel[4]通過試驗分別給出了流動不穩定性時渦發放特點和鈍體尾流形態的概述。Chae[5-6]通過對二自由度下二維水翼的研究，討論了水動力阻尼、非線性流固耦合響應等對水翼振動特性的影響。余志興等[7-8]采用N-S方程以彈簧系統代替實際固體變形產生恢復力，發現要構成翼型渦振，攻角要足夠大。侯磊等[9]采用離散渦方法，分析高雷諾數下來流速度及攻角對水翼渦發放頻率影響規律。劉胡濤等[10]對二維水翼結構進行流固耦合運動分析，探討了初始攻角、剛心位置以及來流速度對水翼振動的影響。郭春雨等[11]采用DEM模型對三維水翼梢渦處流場和氣核運動特性的問題進行數值分析，為梢渦空化初生的機理研究建立基礎。賈文雋等[12]分別采用傳統CFD方法和格子玻爾茲曼流固耦合方法對平直機翼和仿生機翼進行數值模擬，并通過氣結構響應對比找出了仿生機翼的優點及不足。趙宇等[13]采用數值方法對繞水翼的非定常空化流動進行了流動計算分析，結果表明空化現象對水氣兩相轉換起到了促進作用，空化現象影響渦結構空間分布。陳衍茂等[14-15]采用同倫分析法、增量諧波法等研究含有立方非線性的二自由度機翼的極限環顫振，并對極限環的幅值和頻率進行求解。

綜上所述，對于水翼渦振特性的研究主要集中在單一翼型渦振機理等方面的研究，對于相似翼型的渦振特性差異方面存在空白。本文首先將所研究的翼型設置為剛體，探究其泄渦特性，然后通過雙向流固耦合的方法，研究其渦振特性，并對幾種相似翼型進行對比分析，為艦艇舵翼選型提供參考。

2 控制方程及流固耦合求解方法

2.1 流體控制方程

由于舵翼為流線型，后緣產生的渦多為細渦，雷諾平均湍流模型難以捕捉，故采用大渦模擬。大渦模擬綜合采用了直接模擬和雷諾平均模擬的思想與方法。將湍流中的脈動劃分尺度，大尺度湍流直接采用數值求解。而對小于計算網格尺度的湍流模型建立模型求解，其控制方程為：

(1)

(2)

2.2 結構振動控制方程

在本研究中，將三維水翼簡化為二維截面，并引入彈簧阻尼系統，將水翼的振動簡化為豎向和繞旋轉軸扭轉的兩自由度的運動。

(3)

(4)

2.3 雙向流固耦合求解方法

雙向流固耦合即流場計算結果壓力載荷通過流固耦合界面傳遞給結構場，同時結構場的位移變形結果通過流固耦合界面傳遞給流場，雙向流固耦合分析流固耦合交界面處的數據傳遞是雙向的。流場和結構場之間是相互影響的，考慮結構的變形對流場的影響。

本文在計算水翼渦激振動響應的每一個時間步長內，先求解流體控制方程，得到作用在水翼上的水動力FL(t)和力矩Mα(t)，將得到的水動力和力矩代入結構振動方程式。采用Newmark-β法，求解結構的振動響應，利用動網格技術，將得到的速度賦予結構及結構壁面附近的網格，使其隨結構一起做剛體運動，以實現水翼與流場的雙向耦合。

3 物理模型及網格

計算選取了對稱翼型NACA0009、NACA0012和NACA0015，其中重點介紹了NACA0012翼型。NACA翼型末尾兩位數字代表了相對厚度的大小，NACA0015翼型最厚。水翼弦長為0.1 m長，旋轉軸設置在距前緣1/3弦長處，來流攻角為0°。

采用的網格策略為“剛性邊界層運動區域+動網格變形區域+外流場”的劃分策略，翼型表面附有貼體網格，計算Y+值，保證近壁面處網格的質量。翼型外圓形區域為隨動網格，隨翼型一起運動，以保證翼型計算的收斂性及精度。圓環區域為動網格區采用三角形網格，以保證具有較好的運動性。最外圍為流場網格。圖1為所使用網格和局部放大圖。

邊界條件設置：左側弧形邊界以及上下邊界設置為速度入口(velocity-inlet)，右側邊界設置為壓力出口(pressure-outlet)，翼型采用無滑移壁面邊界(wall)。

圖1 網格示意圖

湍流模型選用大渦模擬。計算算法采用“Coupled”，該算法同時求解流體的連續方程、動量方程和能量方程，適合求解本文關于不可壓縮及等溫流動的耦合問題。采用二階迎風格式，以提高計算精度。水翼由于其結構特點，泄渦頻率較高，時間步的選取影響計算精度，本文經過時間步無關性驗證，選取時間步長為0.000 5 s，限于篇幅不再贅述。

本文二維水翼的結構參數取值來自于工程實例。水翼弦長為0.1 m，展長為0.2 m，材料為POM(聚甲醛樹脂)，采用一端固支的方法，基于ANSYS平臺對其提取質量、模態等結構參數。豎彎剛度由式(5)計算得出:

(5)

式中:f為水翼一階豎彎固有頻率，m為水翼單位展長質量。

在對水翼進行模態求解時發現：水翼的扭轉固有頻率要遠大于豎彎固有頻率。豎彎方向的渦振在低速下更容易發生，本文只分析了豎彎方向單自由度的一階渦振現象.本文使用的翼型結構參數取值如表1。

表1 水翼結構參數Table 1 Structural parameters of hydrofoil

4 剛性水翼泄渦特性分析

水翼設置為剛體，分別計算了NACA0012水翼在流速0.5 m/s、1.0 m/s、1.5 m/s、2.0 m/s下的升力系數。圖2、圖3分別為水翼在流速0.5 m/s、1.0 m/s下的升力系數隨時間變化曲線，可以看出，升力系數變化的范圍不大，在計算穩定后，升力系數曲線呈規律的正弦波形，反映了水翼表面受到了周期性變化的垂向載荷。隨著流速的增加，水翼受到的垂向載荷頻率變大。

圖2 0.5 m/s時升力系數曲線

圖3 1.0 m/s時升力系數曲線

對4種流速下的水翼的升力曲線進行快速傅里葉變換(FFT)，得到水翼受到的垂向載荷的頻率，即水翼的泄渦頻率，表2為提取到的各個流速下的泄渦頻率。圖4表示流速與泄渦頻率的關系，可直觀看出泄渦頻率與流速呈現線性關系。

表2 泄渦頻率Table 1 Vortex shedding frequency

圖4 流速與泄渦頻率關系曲線

以上為NACA0012翼型的分析，采用同樣的方法，計算了NACA0009以及NACA0015翼型在同流速下的泄渦頻率，如圖5所示。

圖5 各翼型泄渦頻率曲線

從圖5可以看出，本文選取的3種對稱翼型的泄渦頻率都隨著流速的增加而增加。在同流速的比較下，水翼的厚度對泄渦頻率產生影響，厚度越大的水翼，泄渦頻率越低。

5 彈性水翼渦振特性分析

前文對剛性水翼型的泄渦特性進行了分析，只考慮了流場對水翼的作用，得到的規律較為簡單。本節將水翼設置為彈性水翼，使用雙向流固耦合的方法，對水翼的渦振特性進行分析。

在計算剛性水翼NACA0012時，水翼在1 m/s時泄渦頻率達到了50.37 Hz，與該翼型的自振頻率55.15 Hz十分接近，現在1 m/s左右的區間進行細化，提取水翼在不同流速下的豎向位移圖。

圖6、圖7和圖8分別給出了水翼在0.5 m/s、1.0 m/s、1.5 m/s時的豎向振動時域圖。在低流速時水翼振動較為規律，0.5 m/s時水翼振幅達到最大數值后振幅略有縮小，而后以穩定振幅振動。1 m/s時水翼振幅呈現“喇叭形”，推測在該流速下發生渦振。1.5 m/s時水翼振幅不規則，反映流場在較高流速下湍流度變大，水翼受力情況更復雜。

圖6 0.5 m/s豎向位移曲線

圖7 1.0 m/s豎向位移曲線

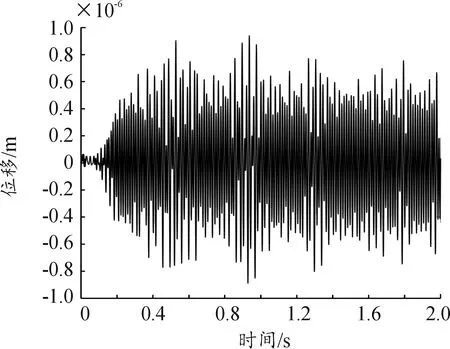
圖8 1.5 m/s豎向位移曲線

圖9—圖11為水翼的振動頻譜曲線。在0.5 m/s的流速下，水翼的振動頻率較低，與前文計算剛性水翼在該流速下的泄渦頻率23.33 Hz相近。在1 m/s時，水翼振動頻率與自振頻率相近，符合發生渦振的特征。隨著流速增加，頻譜圖出現雙峰特征，左側峰集中在水翼的自振頻率附近，呈現明顯寬譜特性，右側峰為水翼的泄渦頻率，較為集中。