基于模糊邏輯的導彈PID/滑模復合控制器設計

陳 喆，呂 瑞，杜 肖，葛云鵬

(中國運載火箭技術研究院，北京 100076)

1 引言

作為彈上核心控制單元，導彈武器的精確打擊離不開優良的自動駕駛儀設計，經過眾多科研工作者長期的設計改良與研究發展，如今導彈自動駕駛儀已經衍生出了多種設計結構，如兩回路結構、三回路結構、PI校正結構、偽攻角控制結構等，控制器設計方法也從古典頻域設計開始向滑模控制、魯棒控制、神經網絡等現代控制方法轉變，各式各樣百花齊放。隨著計算機算力日益提升，甚至在線彈性迭代、機器學習、強化學習等智能方法也在自動駕駛儀設計中逐步得到應用。

由于單一控制器設計方法在有些環境下會存在弊端或出現不優甚至不適用的情況，如文獻[7]針對駕駛儀全包線控制提出了基于動壓插值的綜合增益調度方法，保證了全包線飛行的魯棒鎮定。滑模變結構控制由于響應速度快、魯棒性強等優點，已經廣泛被用來解決各種參數不確定或非線性控制系統問題并取得一定控制效果，但在滑模面附近容易產生抖振。文獻[8]采用滑模控制時則通過切換增益變結構避免了控制量的頻繁抖振。為了提高自動駕駛儀控制能力，各研究人員也在單一控制方法的基礎上加入了多控制復合，如文獻[9-10]針對直/氣控制導彈提出動態面與自適應復合控制方案，解決了多執行機構下的協調配合問題。

控制分配作為復合控制的關鍵決定著控制器性能的優劣，文獻[11-12]通過構造目標函數或控制分配權系數優化模型提出了各自的自適應動態加權分配策略，實現了復合控制的最優分配。考慮模糊邏輯具有對參數攝動不確定性進行逼近的能力，本文從兼顧算法實現及工程應用的角度出發，為提高自動駕駛儀綜合控制性能，提出了一種基于模糊邏輯分配策略的線性PID+滑模復合控制器設計方法，同時也避開了基于現代控制方法的復合控制器設計在建模及實現時都略顯復雜的方式，達到了設計簡單、優勢互補的目的。

2 導彈自動駕駛儀模型

在導彈運動三維非線性模型的基礎上進行通道解耦并線性化，可得到導彈運動的線性模型。以俯仰通道為例，典型的兩回路過載自動駕駛儀結構一般由阻尼內回路和過載外回路兩部分組成，輸出為法向加速度(或法向過載)，其控制回路結構如圖1所示。

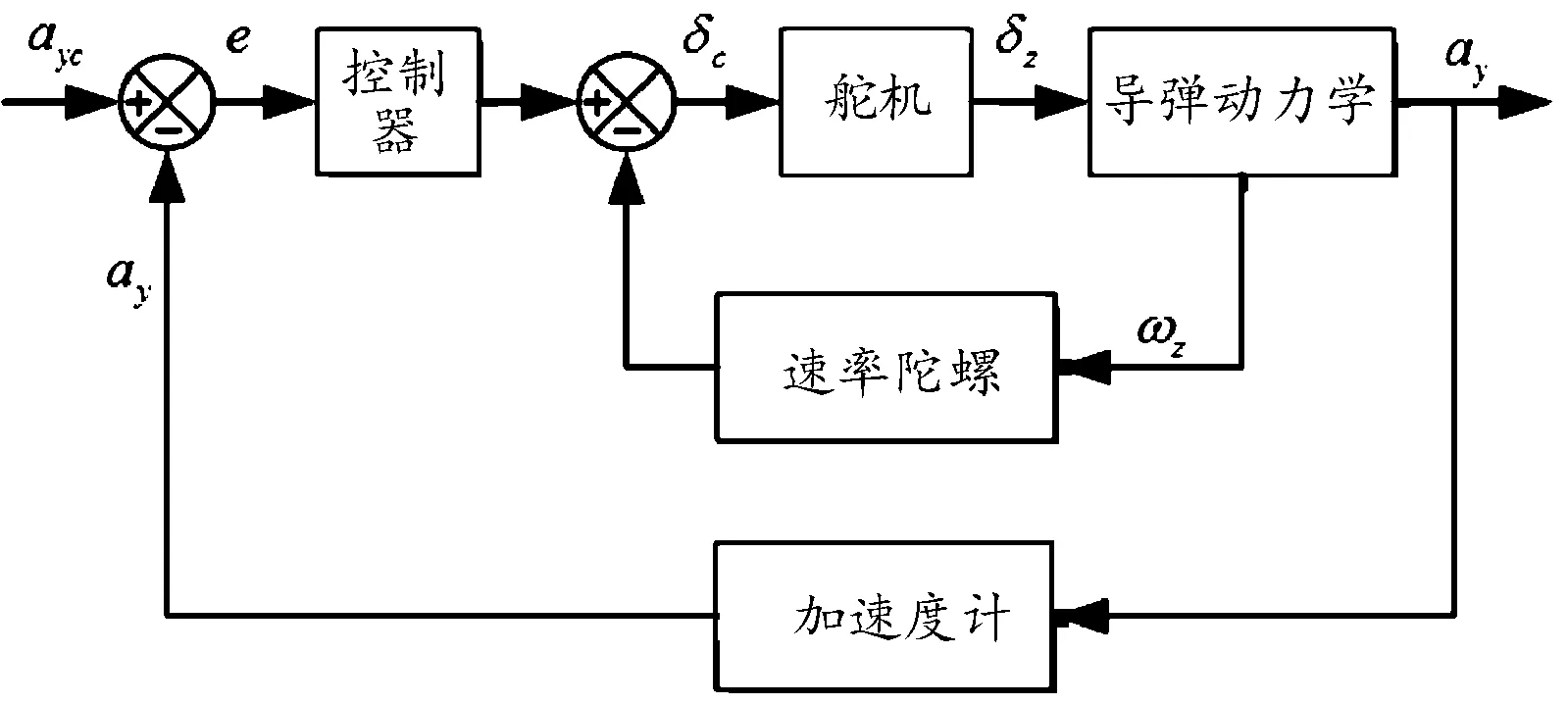
圖1 過載自動駕駛儀控制回路結構示意圖

STT控制方式下過載自動駕駛儀俯仰通道線性化動力學方程為

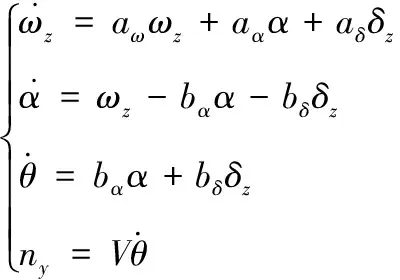
(1)

式中:、、、、分別為與導彈飛行相關的動力學參數；、、、分別為導彈的俯仰角速率、飛行攻角、彈道傾角以及俯仰舵偏角；、則為導彈速度與法向加速度。

將方程式(1)左右兩邊分別進行Laplace變換，可以得到關于彈體動態特性的傳遞函數為

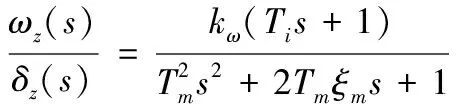
(2)

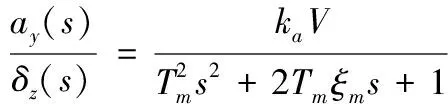
(3)

其中:、為彈體開環時間常數與阻尼系數；為攻角滯后時間常數；、分別為相應傳遞函數中的比例系數，具體表達式如下

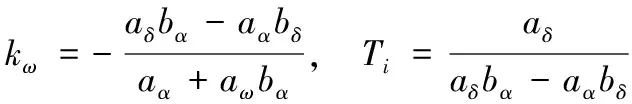
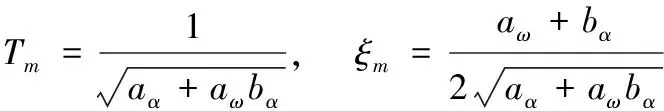
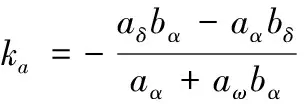
3 單一控制方式設計

3.1 線性PID控制設計

傳統的兩回路過載自動駕駛儀是0型系統，雖然響應速度快但存在一定的穩態誤差，若在控制回路中加入PI校正，則能更好的跟蹤輸入變化，減小系統本身存在的靜差，類似于三回路自動駕駛儀的積分增穩回路。線性PID控制自動駕駛儀回路如圖2所示。

圖2 線性PID控制自動駕駛儀回路結構示意圖

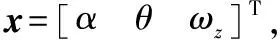
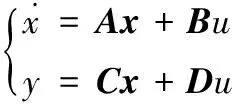
(4)

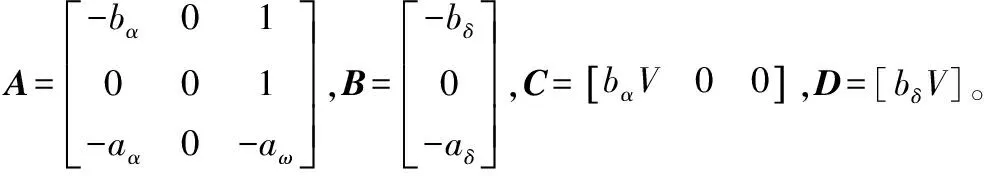
對于線性PID控制自動駕駛儀，極點配置方法是設計控制參數的一種有效手段，若采用如圖3所示的狀態反饋方式。

則狀態反饋下受控系統的輸入為

=-x+′

(5)

式中：為狀態反饋增益矩陣，′為期望狀態值。

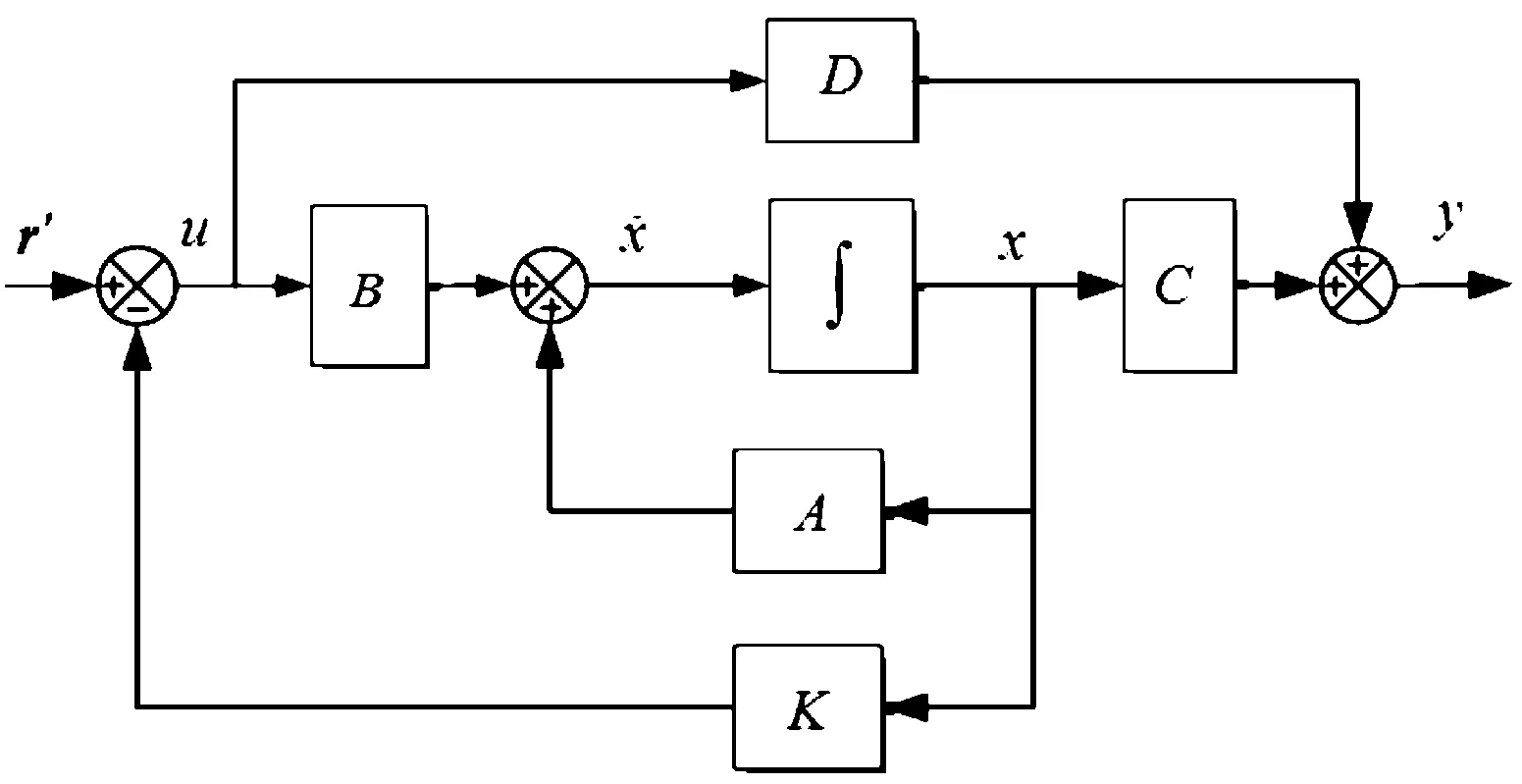
圖3 狀態反饋結構示意圖

若采用如圖4所示的輸出反饋形式。

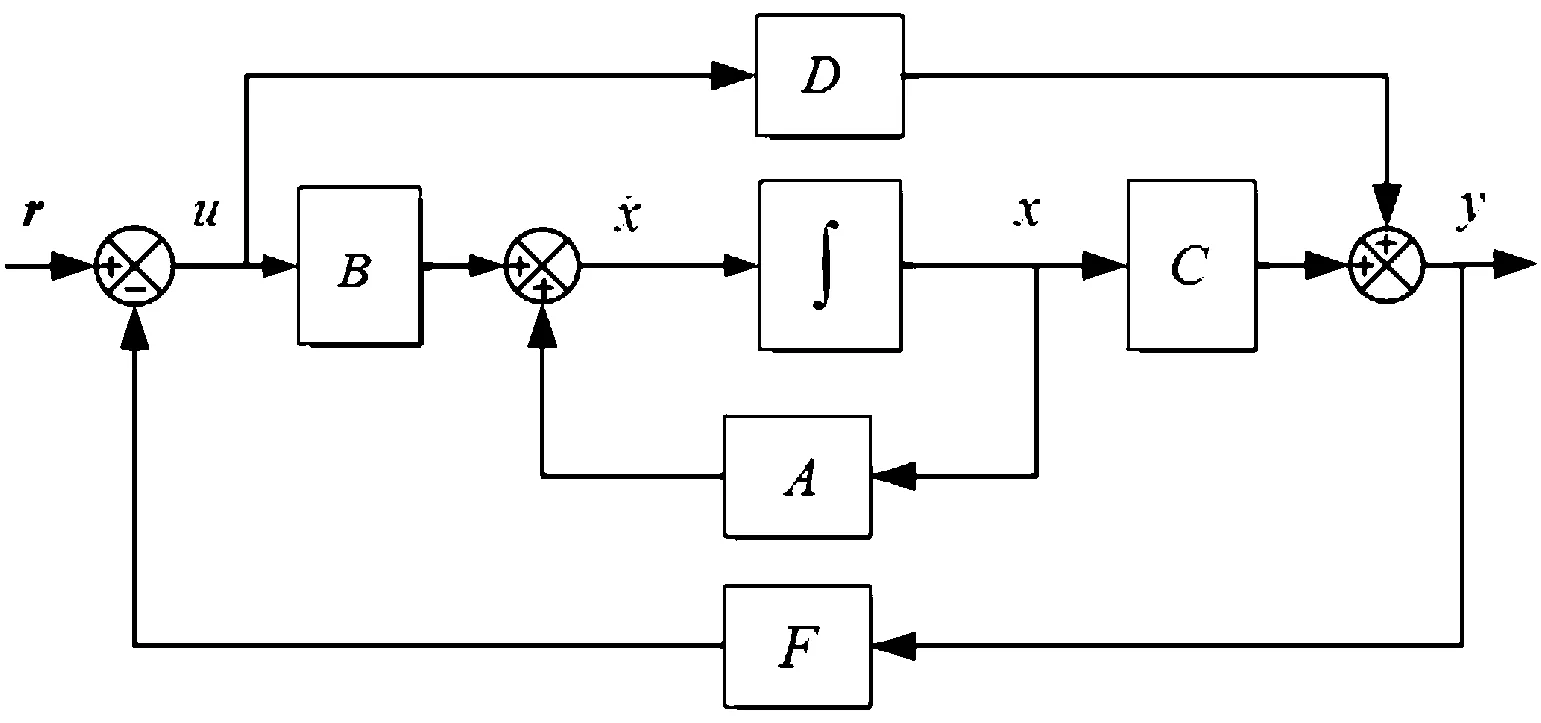
圖4 輸出反饋結構示意圖

則輸出反饋下受控系統的輸入為

=-y+

(6)

其中：為輸出反饋增益矩陣，為期望輸出值。設系統的輸出反饋可用狀態反饋實現，由式(4)與式(5)可知=-((-u))+′，展開后可得

=-(-)+(-)′

(7)

記=(-)′，則輸出反饋的增益矩陣為

=(-)

(8)

進行參數設計時可將自動駕駛儀各回路反饋值疊加到圖2舵偏角位置，并用狀態變量、、來描述

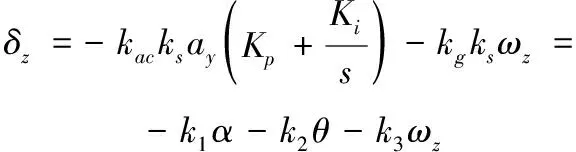
(9)

其中、、為狀態反饋增益矩陣的子元素，具體如下:

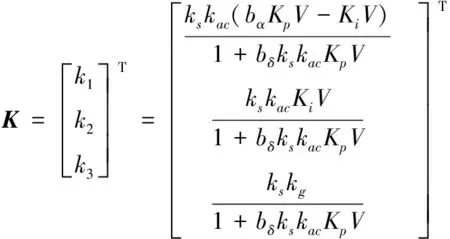
(10)

根據矩陣及式(8)則可求得輸出反饋增益矩陣為

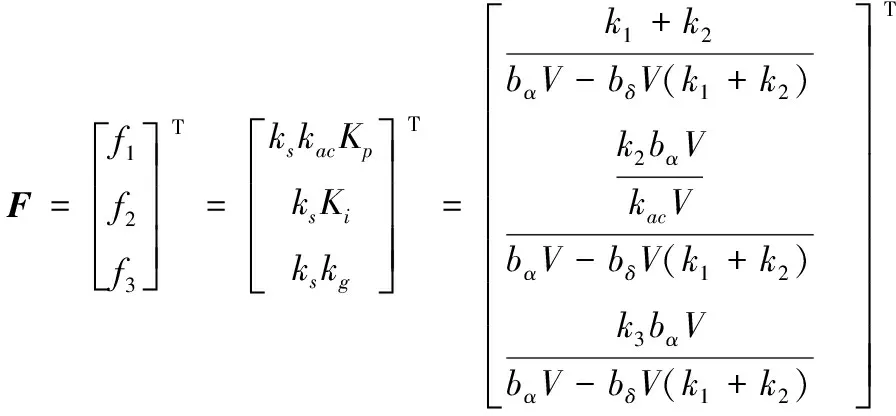
(11)

因此帶PI校正的兩回路過載自動駕駛儀設計參數為

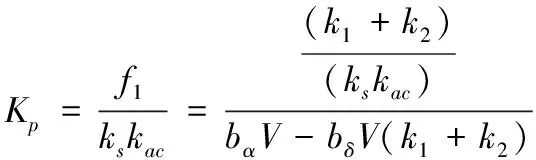
(12)

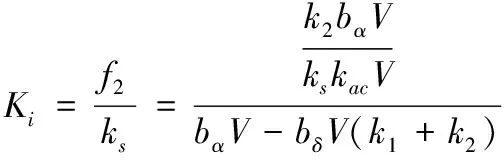
(13)

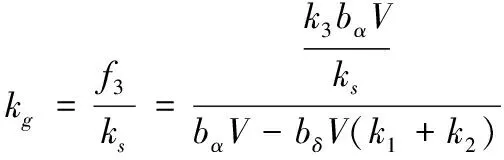
(14)

3.2 滑模變結構控制設計

在帶PI校正過載自動駕駛儀控制結構上引入滑模控制，則控制魯棒性可得到增強，彈體相關的傳遞函數與PID控制自動駕駛儀相同，如圖5所示。

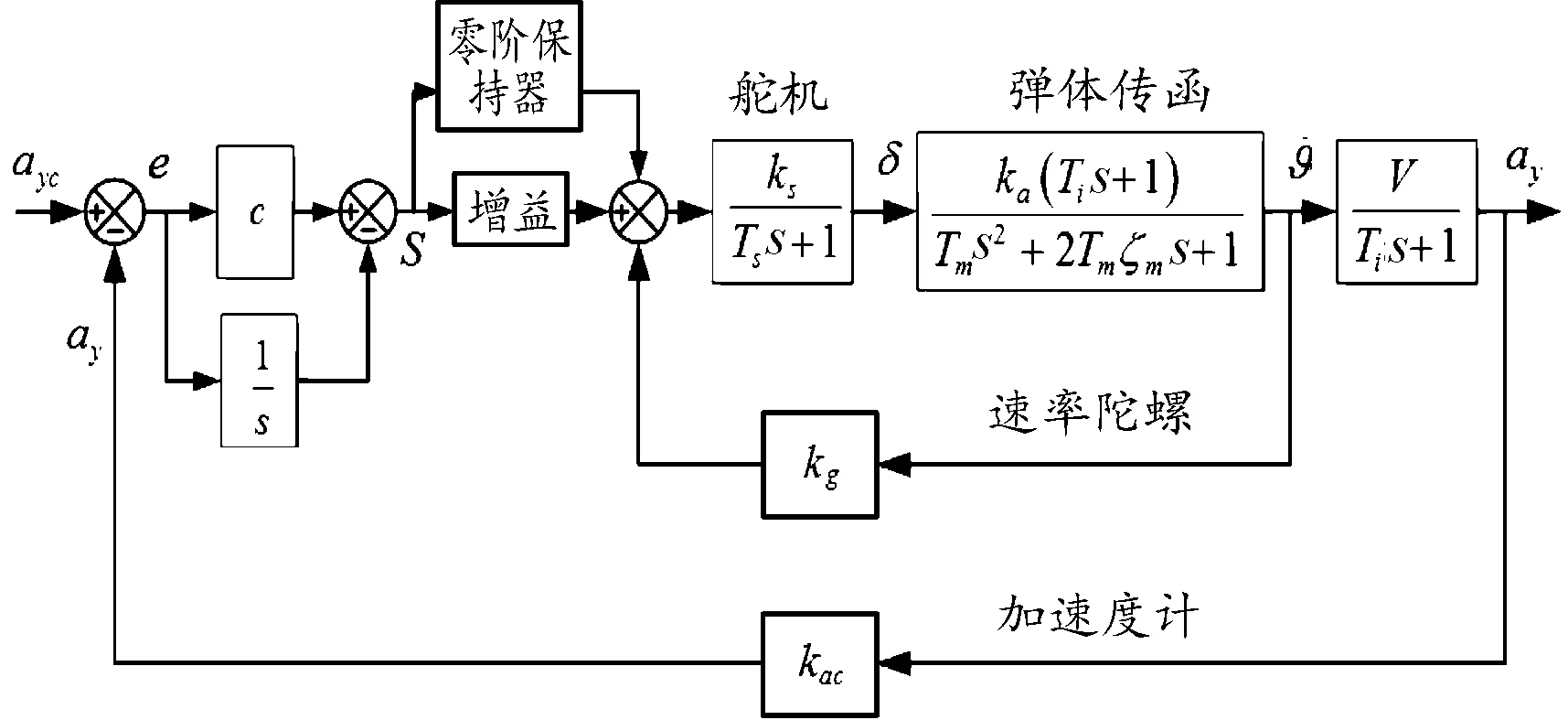
圖5 滑模控制自動駕駛儀回路結構示意圖

根據式(3)的被控對象傳遞函數經Laplace反變換有

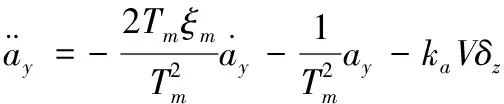
(15)

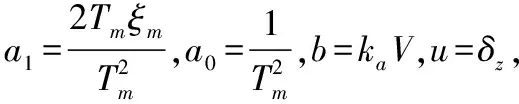
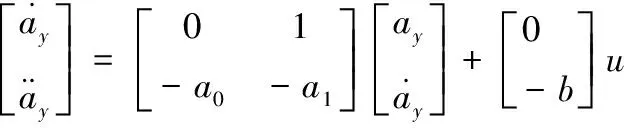
(16)

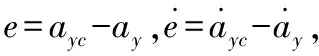
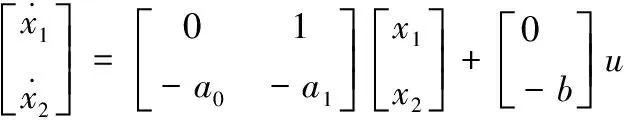
(17)

滑模面采用如下函數：

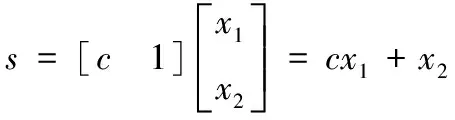
(18)

切換函數采用誤差比例切換

=·||·sgn()

(19)

式中: sgn為符號函數；為比例切換系數，根據誤差大小調節能夠實現過載快速控制，并有效地抑制滑模系統抖振的幅值。

4 模糊邏輯復合控制器設計

基于上述線性PID與滑模控制設計，在自動駕駛儀上融合這2種設計思想，通過過渡切換實現取長補短，得到魯棒性更強、適用范圍更廣的PID/滑模復合控制自動駕駛儀，如圖6所示。

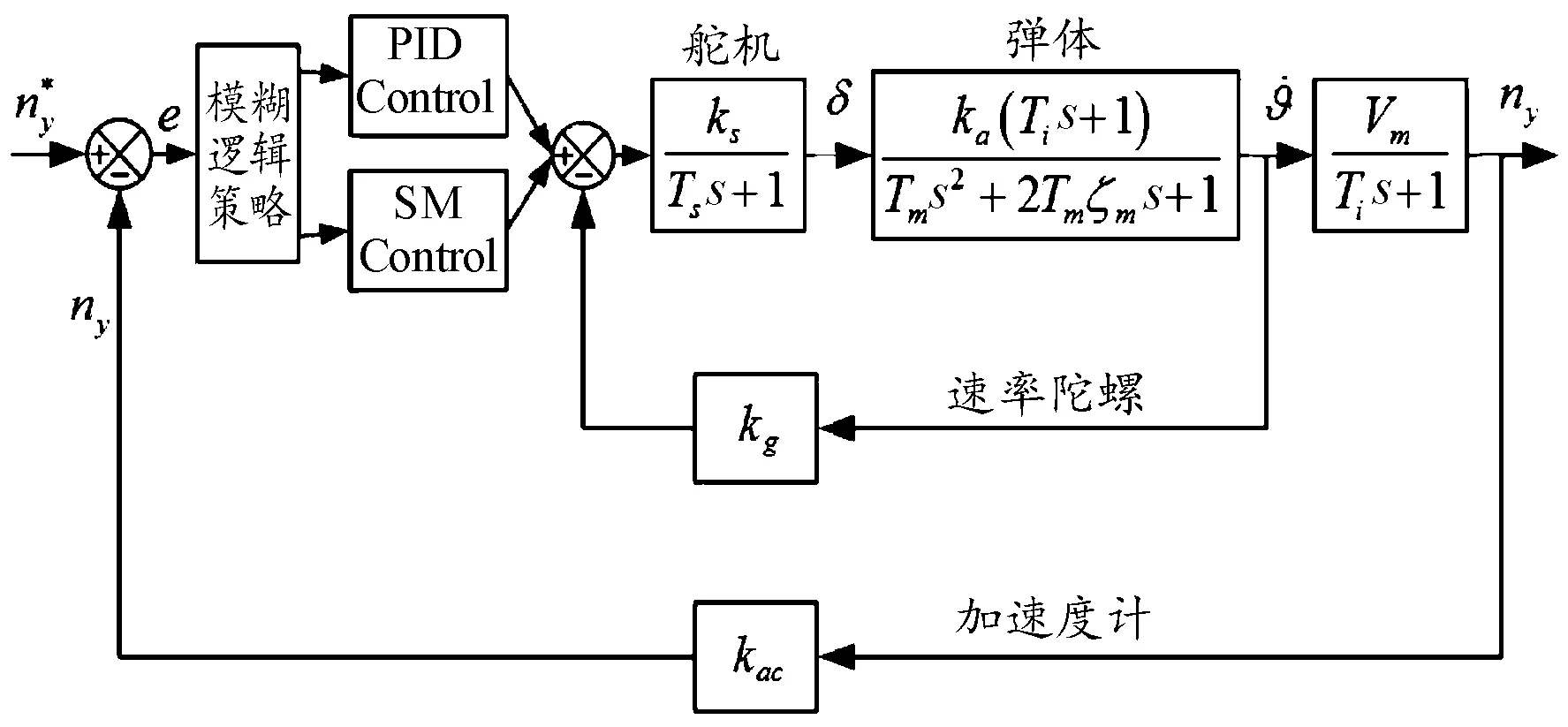
圖6 PID/滑模復合控制自動駕駛儀回路結構示意圖

使用多控制器復合時類似于多執行機構復合，會涉及到控制的協調與分配問題，由于模糊控制具有對參數攝動不確定性進行逼近的能力，因此在自動駕駛儀復合控制分配策略上采用模糊邏輯對2種控制的切換使用進行權值分配設計。由于存在參數攝動時控制需求體現在過載及攻角上的變化較為明顯，以自動駕駛儀的過載誤差及攻角大小作為模糊邏輯的輸入參考量，以滑模控制的權值(,)作為參考輸出。則PID控制與滑模控制各自的控制輸入量可表示為

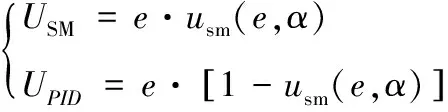
(20)

式中：為滑模控制輸入量；為PID控制輸入量；為自動駕駛儀全局控制誤差；(,)為滑模控制分配的權值，范圍0～1，取0時表征完全采用PID控制，取1時表征完全采用滑模控制。外部飛行環境變化時根據采用的模糊規則對自動駕駛儀復合控制進行增益調節。

對于模糊邏輯隸屬度函數的設置，模糊區間采用等距劃分，為了使復合控制的切換平緩穩定，隸屬度函數取為高斯函數，在攻角輸入的論域上定義5個子集：、、、、；在過載偏差輸入的論域上定義4個子集：、、、；滑模控制分配輸出的論域上定義5個子集：、、、、，具體如圖7所示。其中，輸入參考量過載誤差及飛行攻角的隸屬度函數曲線寬度相對較大，適合于較大范圍的平穩過渡；輸出量滑模控制的權值函數曲線寬度相對較小，便于不同環境下的控制側重使用。

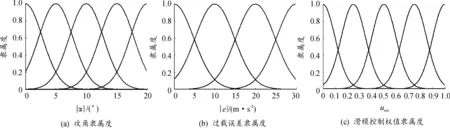
圖7 模糊邏輯輸入輸出參考量隸屬度函數曲線

為了使控制權值的變化比較平滑，避免控制律切換對系統穩定性造成影響，需要對模糊邏輯規則進行優化，經過優化后得到模糊控制規則如表1所示。

表1 控制分配模糊規則表Table 1 Fuzzy rule of control allocation

5 仿真驗證與分析

結合以上推導與復合控制設計方法，以某導彈機動飛行段為例進行仿真研究及分析。導彈飛行速度介于2.0～3.2，飛行攻角絕對值在0°～18°之間，自動駕駛儀相關控制參數設計以表2中某末制導特征點動力系數為準。

表2 導彈某特征點動力系數Table 2 Dynamic coefficients of feature point

舵機模型參數=-0.013、=0.01，控制參數=1.4，=6.5，=34.1，=9.9，=1.5，表2特征點處導彈期望的法向加速度大小(加速度指令)為13.18 m/s，飛行環境氣動參數攝動在-20%～+20%的范圍。

根據給出的仿真條件，按上文提到的3種自動駕駛儀設計方法：單獨PID控制；單獨滑模控制；PID+滑模復合控制，得到控制器在參數攝動下的響應結果如圖8—圖10所示。

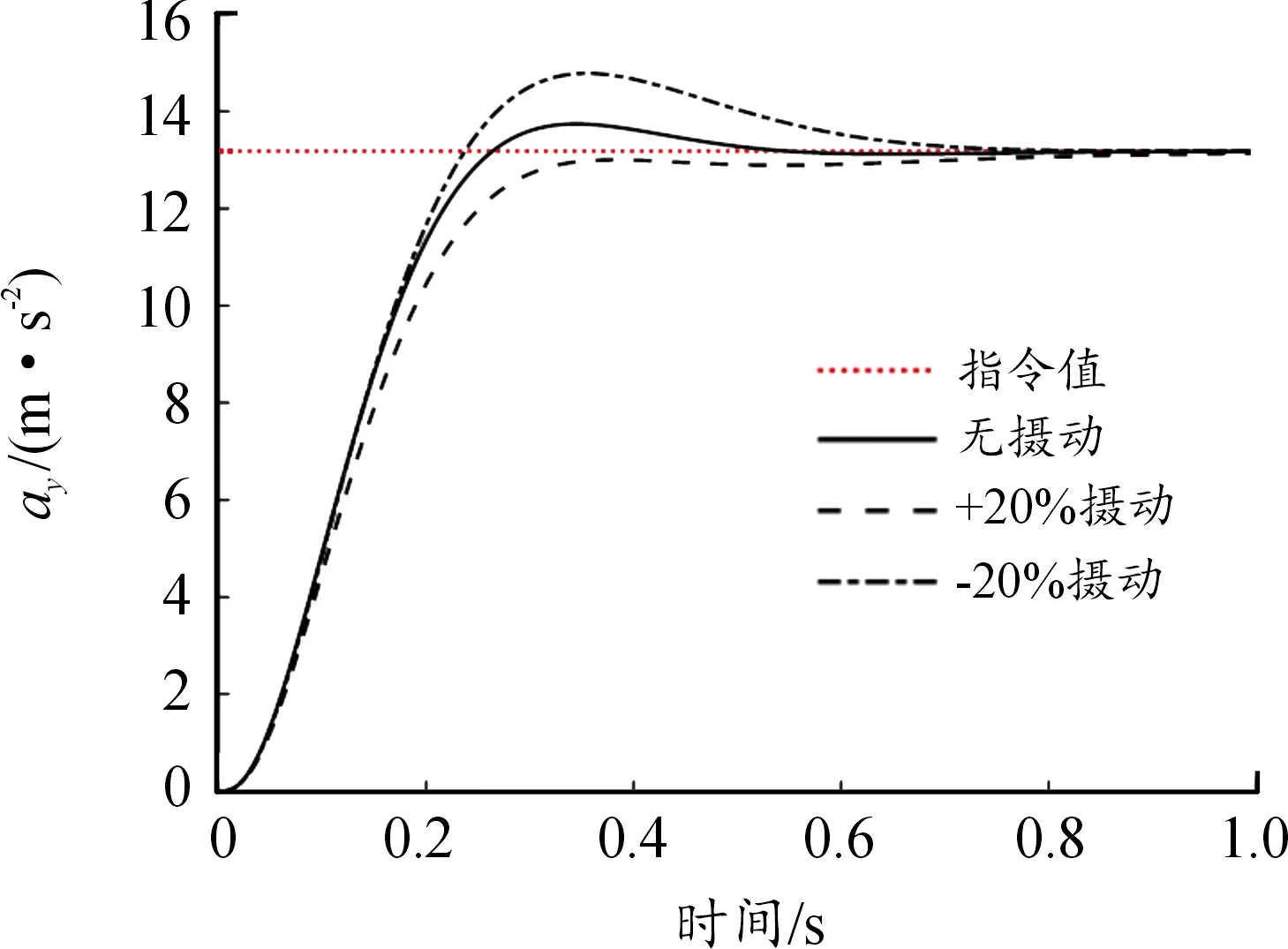
圖8 PID控制自動駕駛儀過載響應曲線

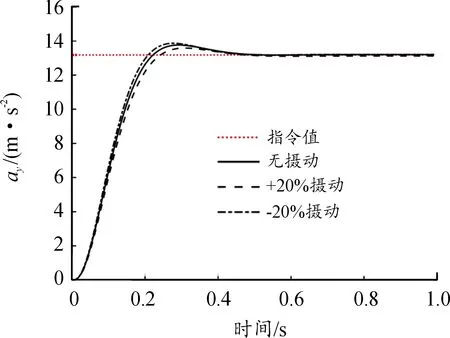
圖9 滑模控制自動駕駛儀過載響應曲線

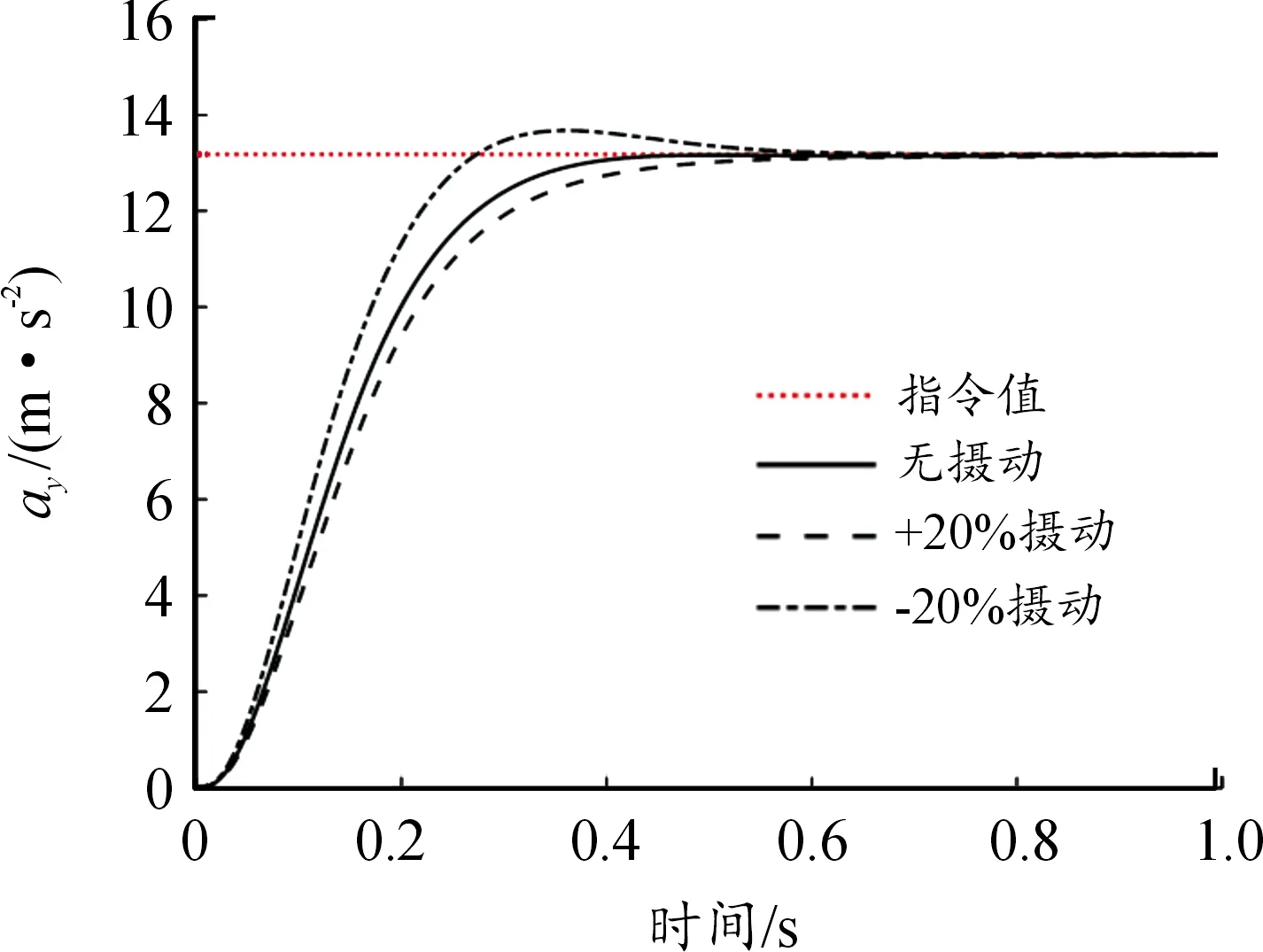
圖10 復合控制自動駕駛儀過載響應曲線

3種控制模式在+20%參數攝動下的上升時間與超調量對比如表3所示。

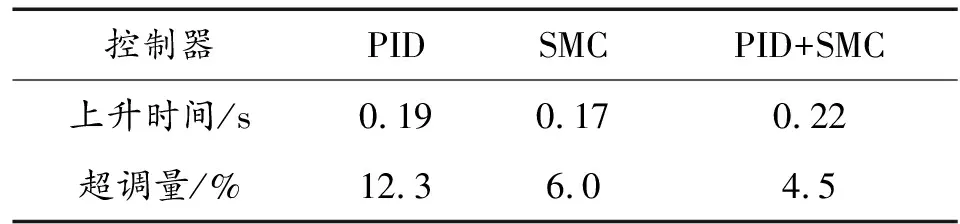
表3 上升時間與超調量對比Table 3 Comparison of rise time and overshoot

仿真結果中圖8—圖10的自動駕駛儀過載響應曲線較明顯地體現了3種自動駕駛儀在同一環境下的響應能力及參數攝動對控制器效果的影響。滑模控制相對不敏感，復合控制則居于PID控制與滑模控制之間。

復合控制權值分配及舵偏響應如圖11、圖12所示。

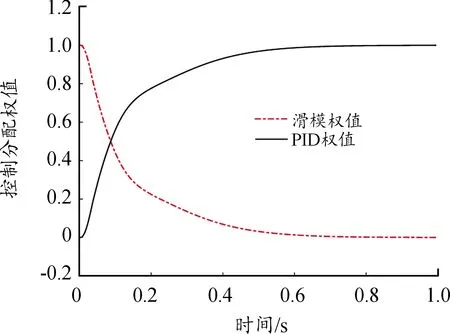
圖11 復合控制權值分配曲線

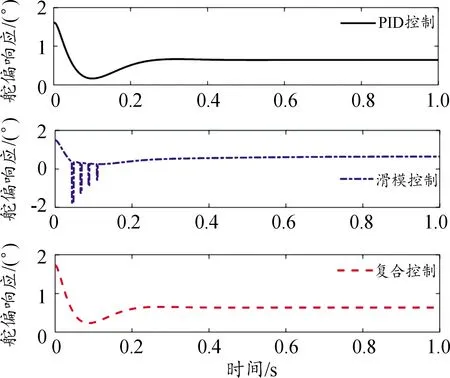
圖12 復合控制舵偏響應比較曲線

從圖11、圖12仿真結果來看，采用復合控制策略時，控制偏差相對較大時滑模控制占主導，快速縮小控制誤差。隨著誤差逐漸收斂，圖11中大概在0.1 s時刻控制器作用效果開始轉變，控制器分配權值開始向PID控制傾斜，逐步達到穩態精確控制。在未知飛行環境出現參數攝動的情況下，相比單一控制方法，該PID/滑模復合控制自動駕駛儀集各家所長既不失控制精確性，也具備較強魯棒性，控制效果有較好提升。

6 結論

為提高過載自動駕駛儀在參數攝動情況下的控制魯棒性，本文提出的PID+滑模復合控制器設計方法通過模糊邏輯策略根據過載誤差及飛行攻角調整復合控制的分配權值，實現了控制器隨外部參數攝動變化自適應調整控制分配的目的，且兼具快速響應與強魯棒性的特點。與傳統單一控制方法進行比較，仿真結果驗證了該復合控制器在滿足控制穩定需求的同時，對于飛行環境中參數攝動具有較強的適應能力，提升了導彈的綜合控制性能。