新型彈性膠泥-液壓浮動機的優化設計

李煥斌，曹廣群，李 強，李帥龍

(中北大學 機電工程學院，太原 030051)

1 引言

在現代戰爭中，高射速自動機廣泛應用于艦炮、航炮中，是防空反導的主要武器。但在自動機射速提高的同時，會帶來后坐力增大以及射擊精度下降的問題。因此減小自動機后坐力的同時提高射擊精度是高射速自動機一個重要的研究方向。浮動技術的應用就是主要的技術手段之一，與炮口制退器減少后坐能量的方式不同，浮動技術是通過在自動機在復進過程中擊發來減小后坐動能；即擊發時自動機有一定的復進速度，自動機的后坐能量先被復進能量抵消，剩余的能量產生后坐，擊發時的復進速度越大，減少的后坐能量越多。采用浮動技術能夠減少自動機復進到位時對炮架的沖擊，提高射擊時的穩定性，顯著的提高武器的射擊精度。

浮動機是實現浮動技術的裝置，是自動機的組成部分。常見的浮動機有彈簧式、彈簧液壓式、液體氣壓式等。彈簧式浮動機結構簡單，但是耗能較小，浮動穩定性較差；彈簧液壓式浮動機吸能大、適應性強，但采用彈簧為復位元件，故存在尺寸大，壽命短的不足；液體氣壓式浮動機受溫度的影響較大，且不易密封。

彈性膠泥是一種新型的功能材料，具有高阻尼粘彈性、可壓縮性和流動性，以及耐老化穩定性能和耐高低溫性能，且具有液體固體的2種屬性，在航空、航天、兵器、船舶、車輛等領域有著廣泛的應用。比如車擋緩沖器、鐵路火車上的膠泥緩沖器等。用彈性膠泥作為工作介質的減后坐裝置對速度變化的響應較快，能夠快速有效地衰減振動和吸收沖擊能量，將彈性膠泥應用到浮動機上，從而代替彈簧液壓浮動機的彈簧部分，利用彈性膠泥的可壓縮性為復位元件和彈性膠泥的高阻尼特性為阻尼元件。不僅可以在后坐時消耗后坐能量，還能存儲復進的能量，消除彈簧的疲勞現象，實現無磨損工作，從而提高使用壽命。

本研究以轉管炮為例，設計了一種新型的彈性膠泥-液壓浮動機，其中彈性膠泥作為彈性模塊和粘滯阻尼模塊，液壓部分作為液壓阻尼模塊。根據模塊間的載荷特性，通過粒子種群算法對影響浮動機性能的結構參數進行尋優。基于此結構參數建立浮動部分的運動模型，對自動機的后坐運動特性進行仿真分析。

2 浮動機結構及原理

2.1 浮動機結構的選取

浮動機浮動方式采取首發不浮動的完全浮動式，擊發方式為近似定速定點擊發，后坐方式為桿后坐，它主要由彈性膠泥模塊、液壓阻尼模塊、液量調節器3部分組成。浮動機的結構如圖所示，主要由液壓阻尼器活塞、液壓阻尼器活塞桿、活門、彈性膠泥活塞、彈性膠泥活塞桿、針形桿等組成。浮動機的結構原理如圖1所示。

1-液壓活塞桿;2-針形桿;3-活門;4-流液孔;5-液壓活塞;6-節流孔;7-彈性膠泥活塞桿8-彈性膠泥活塞;9-阻尼孔;10-彈性膠泥;11-連接頭;12-液量調節器

2.2 浮動機工作原理

1) 射擊過程

在膛底合力的作用下，炮箱帶動液壓活塞桿和彈性膠泥活塞桿向后運動。

2) 后坐過程

對于液壓阻尼模塊：液壓活塞桿向后運動，活塞擠壓Ⅰ腔中的液體，使Ⅰ腔成為工作腔，此時Ⅰ腔中的液體分成兩股流向Ⅱ腔，第一股經過活塞上的單向活門流液孔流向Ⅱ腔；第二股經活塞通過針形桿與活塞桿構成的可調流液孔間隙經活塞內腔流向Ⅱ腔。在液體阻力的作用下，液壓活塞桿以及炮箱的運動受到阻力而減速。

對于彈性膠泥模塊：彈性膠泥活塞桿向后運動，活塞壓縮彈性膠泥，膠泥吸收能量轉化為彈性勢能。同時彈性膠泥從Ⅲ腔通過阻尼孔流向Ⅳ腔進而消耗后坐能量。

3) 復進過程

對于彈性膠泥模塊，由于先前存儲了彈性勢能，彈性膠泥體積膨脹推動活塞桿及炮箱向前運動，同時彈性膠泥從Ⅳ腔通過阻尼孔反向流動到Ⅲ腔消耗部分能量。

對于液壓阻尼模塊，液壓活塞擠壓Ⅱ腔中的液體，使Ⅱ腔成為工作腔，迫使Ⅱ腔中的液體流向Ⅰ腔。由于活門簧及液體壓力的作用，活門向前運動，關閉活塞上的流液孔，這樣Ⅱ腔中的液體只能通過活塞桿上的可調流液孔流向Ⅰ腔，從而產生較大的復進阻力減慢炮箱的復進，使炮閂在炮箱復進過程中復進到位，閉鎖擊發下一發炮彈，實現浮動射擊。

3 浮動機動力學模型

3.1 彈性膠泥力學模型

彈性膠泥既有彈性儲能的特性，也具有粘滯耗能的特性，能夠承受靜態載荷。浮動機彈性膠泥的阻抗力由彈性力和阻尼力兩部分組成，其力學模型可以用Kelvin-Voigt模型來表示，如圖2所示。

該模型由變剛度的彈性原件和阻尼力隨速度變化的阻尼原件構成。其中為彈性回復力，為粘滯阻尼力，為浮動機的位移，為浮動機總的受力，滿足：

=+

(1)

圖2 彈性膠泥力學模型示意圖

1) 彈性回復力

彈性膠泥的彈性性能是由于粘滯介質在壓力的作用下壓縮產生的，同時由于膠泥的壓縮率是隨著外力的變化而變化的，所以浮動機由于粘滯介質的壓縮性產生的剛度是一個動態的剛度。彈性膠泥受到的壓強與其壓縮率有關，由于在發射時浮動機要承受較大的發射載荷，因此選用的粘滯材料需要有較大的剛度來產生較大的緩沖力，經對比分析，選取粘度為12 500 mm/s的甲基硅油作為粘滯材料，其壓縮率隨壓強的變化數據如表1所示。

表1 壓縮率與壓強關系Table 1 Relation between compression rate and pressure

為得到在任意壓縮率下的壓強值。對表1數據進行插值擬合得到在粘度為12 500 mm/s時壓強隨壓縮率變化的關系式為：

=3.718×10+4 397+890.8-2.182

(2)

根據該關系式得到壓強隨壓縮率變化的曲線如圖3。

圖3 壓強-壓縮率擬合曲線

參考已有的對彈性膠泥彈性力的計算模型，設浮動機彈性膠泥部分活塞半徑為，活塞桿的半徑為，活塞的厚度為，活塞的作用面積為，彈性膠泥阻尼器的缸體長度為，浮動機后坐位移為，忽略活塞上小孔對彈性膠泥體積的影響，則膠泥的體積為:

(3)

(4)

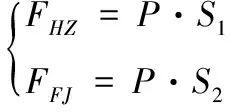
(5)

其中：為后坐時彈性力；為復進時彈性力。

彈性膠泥的預壓力是其基本參量，當外界載荷小于預壓力時，活塞靜止不動，當外界載荷大于預壓力時，活塞運動。設彈性膠泥的預壓力大小為，則后坐時總的彈性力為=+，復進時總的彈性力為=+。

2) 粘滯阻尼力

粘滯阻尼力的大小與粘滯介質的種類、阻尼器的結構、活塞的運動速度等因素有關。粘滯阻尼力由孔縮效應產生的阻尼力和粘滯摩擦產生的阻尼力構成。阻尼力大小=1+2，其中為孔縮阻尼系數，為粘滯摩擦阻尼系數。和為速度指數。

由孔縮效應產生的阻尼力為：

(6)

其中：為孔隙衰減系數；為活塞的直徑；為活塞桿直徑；∑為總損失系數；為阻尼孔直徑；為阻尼個數；為粘滯介質密度。

由粘滯摩擦產生的阻尼力為：

(7)

其中：為粘度衰減系數；為活塞厚度；為每組阻尼孔直徑；為稠度系數。

綜上可得粘滯阻尼力的大小=+。

3.2 液壓阻尼力學模型

在進行液壓阻尼力的計算時，做如下假設：

1) 液體不可壓縮。

2) 液體的流動是一維定常的。

3) 各個流液通道的流動具有一致性。

4) 忽略液體經過流液孔的收縮現象。

5) 流經流液孔的液體能量損失與液體內能成正比。

根據液體連續方程：

(8)

其中：為液體相對于活塞的速度；為活塞的工作面積；為后坐流液孔總面積；為活塞運動的速度。

則液體的絕對速度：

(9)

由于液體具有壓縮性，因此設后坐時Ⅰ腔活塞截面壓力為，流速=0，Ⅱ腔活塞截面壓力=0，而有流速，則根據伯努利方程，Ⅰ腔和Ⅱ腔壓力和流速的關系式為：

(10)

其中為后坐能量損失系數；=1+，為引用的后坐液壓阻力系數。

(11)

3.3 后坐運動分析

后坐部分運動時的受力模型如圖4所示。

圖4 浮動機后坐部分的受力模型示意圖

由圖4可知，后坐部分的受力有炮膛合力；后坐部分的重力；搖架對后坐部分的約束力；后坐部分與導軌的摩擦力；浮動機對后坐部分的彈性力、粘滯阻尼力、液壓阻尼力。

浮動機的運動分為4個時期：

1) 后坐加速時期：從后坐速度=0到=，該階段的后坐行程為；

2) 后坐減速時期：從后坐速度=到=0，該階段的后坐行程為；

3) 復進加速時期：從復進速度=0到=，該階段的復進行程為；

4) 復進減速時期：從復進速度=到=0，該階段的復進行程為。

后坐部分的運動方程為：

式中：為后坐阻力。

后坐時：=++++-sin

復進時：=---+-sin

4 基于粒子種群算法的浮動仿真分析

4.1 粒子種群算法

粒子群算法是進化算法的一種，將粒子比作鳥群，每個粒子被賦予速度和位置，每個粒子在空間中獨立的搜索最優解，將其作為自身的個體極值。每個粒子將個體極值與其他粒子分享，將最優的個體極值作為全局的最優解。每個粒子根據個體極值與全局最優解不斷調整自己的速度和位置，也就是反復進行迭代的過程，最終通過達到最大迭代次數或全局最優位置滿足最小界限時結束尋優。

在尋找個體極值和全局最優值的過程中，粒子的速度和位置更新公式如下：

(12)

式中：和為學習因子；和為[0，1]范圍內的隨機數；為慣性因子；為第個粒子個體最優解的維分量；為第個粒子群體最優解的維分量；為第個粒子位置的維分量；為第個粒子速度的維分量。

速度更新公式由3部分組成：第1部分為慣性部分，表示粒子有維持自己先前運動的趨勢；第2部分為自我認知部分，表示粒子具有向著自己歷史最優位置逼近的趨勢； 第3部分為群體認知部分，表示粒子有向著群體歷史最優位置逼近的趨勢。粒子種群算法的優化流程如圖5所示。

圖5 優化流程框圖

4.2 優化變量和目標函數的選取

根據浮動機的結構計算分析以及結構具體實現的可能性，選取浮動機的優化結構參數如表2所示。

對于浮動機的設計，后坐力和后坐長度的大小是評價浮動機性能好壞的指標。但是現有的研究表明，在目前對浮動機結構優化中很難同時將后坐長和最大后坐阻力降到最小，想要后坐位移最小，不可避免的會引起后坐阻力的增大。因此參考現有浮動機的設計理論，將后坐長度作為邊界條件，限制在一定的范圍內。將最大后坐阻力作為目標函數進行尋優。

表2 浮動機的優化結構參數Table 2 Optimal structural parameters of floating device

4.3 優化及仿真分析

選取種群數目為500，最大迭代次數為500，慣性權重取0.8，自我學習因子為0.5，種群學習因子為0.5進行尋優計算，全局最優個體的最大阻尼力的最小值隨迭代步數的收斂曲線如圖6。

圖6 后坐力的收斂曲線

從圖6可以看出，隨著迭代次數的增加，最大后坐阻力值開始遞減收斂，最終收斂于24 454 N。從而得到在該最小后坐阻力下對應的浮動機結構參數如表3所示。

表3 尋優后的浮動機結構參數Table 3 Optimized structural parameters of floating device

該自動炮的射速為600發/min，后坐部分的質量為500 kg，在射角為0°的情況下，忽略射擊時溫度的變化對浮動機性能的影響，將上述尋優后的結構參數作為初始條件，對浮動部分的運動進行10連發的仿真，得到10連發時的后坐位移、后坐速度和后坐阻力的曲線如圖7所示。

從圖7可以看出：由于首發射擊時不需要浮動，浮動部分從原始位置開始后坐，后坐到位后在復進過程中擊發。而以后的連發射擊中浮動部分保持穩定的浮動，所以第一發的后坐沖量較大，后坐長和后坐力也大于以后的連發射擊。浮動部分的首發最大后坐位移為42.4 mm，首發最大后坐速度為1.75 m/s，最大復進速度為0.5 m/s，首發最大后坐阻力為24 454 N。

當射擊穩定后，每一發的擊發位置在12 mm上下微小波動，擊發時的復進速度在0.5 m/s上下微小波動，因此該浮動機實現了近似的定點定速擊發，保證了浮動的穩定性。驗證了模型動力學參數匹配的正確性。該浮動機實現了后坐部分達到最大復進速度時擊發，能夠最大的消耗后坐能量，減小后坐力。穩定射擊時的后坐長度為23 mm，最大后坐速度為1.25 m/s，最大后坐阻力為20 585 N，滿足設計要求。

圖7 后坐特性優化曲線

4.4 后坐特性對比

原浮動機采用彈簧-液壓結構，其結構參數如表4所示。

表4 原浮動機結構參數Table 4 Structural parameters of original floating device

在初始邊界條件不變的情況下，對比原彈簧-液壓式浮動機與彈性膠泥-液壓浮動機的后坐部分的后坐位移、后坐速度、后坐阻力隨時間變化的曲線如圖8所示。

從圖8中得到彈簧-液壓式浮動機和彈性膠泥-液壓式浮動機的后坐特性參數如表5所示。

根據表4得到彈性膠泥-液壓浮動機相比于彈簧-液壓浮動機，后坐特性參數的下降比率如表6所示。

可以看出：相比于彈簧液壓式浮動機，采用彈性膠泥-液壓浮動機后，首發的最大位移、速度、后坐阻力以及穩定發射后的后坐阻力、后坐長度、后坐復進速度都得到明顯的下降，該浮動機能夠提高自動炮的減后坐能力。

圖8 后坐特性對比曲線

表5 后坐復進參數Table 5 Comparison of recoil reentry parameters

表6 后坐特性參數的下降比率Table 6 Reduction ratio of recoil characteristic parameters

5 結論

根據彈性膠泥具有的彈性特性和阻尼特性，提出一種用于高射速武器的新型彈性膠泥-液壓浮動機，建立了浮動機彈性膠泥部分的彈性力和阻尼力模型以及液壓部分的阻尼力模型，對其中重要的參數進行了推導；對浮動部分進行了動力學模型的建立，得到浮動部分在不同時期的運動規律；基于粒子種群算法，以影響浮動性能的結構參數為自變量，后坐阻力為目標函數，對浮動結構進行優化；通過優化后的模型，對浮動機進行十連發射擊后坐運動的仿真，得出以下結論：

1) 彈性膠泥-液壓浮動機可以滿足浮動自動機的發射要求，該浮動機實現了在后坐位移為12 mm，復進速度為0.5 m/s時的近似定點定速擊發，后坐阻力和后坐位移符合要求，實現了浮動循環的穩定性；

2) 與彈簧-液壓式浮動機相比，采用彈性膠泥-液壓浮動機能夠降低首發和穩定射擊時的最大后坐阻力和最大后坐長度，驗證了彈性膠泥代替彈簧方案的可行性。

3) 使用彈性膠泥-液壓浮動機，能夠增大后坐能量的吸收率，而且膠泥的阻抗力可以通過調節浮動機的結構參數以及膠泥的性能參數調節，來滿足不同后坐阻力的要求，可為彈性膠泥在浮動機上的應用提供參考。

由于彈性膠泥-液壓浮動機結構的多樣性，其數學模型也不盡相同，需要將不同結構的彈性膠泥-液壓浮動機應用于火炮的減后坐研究中；基于彈性膠泥在浮動機上的應用，可以考慮將彈性膠泥材料用于火炮的減振中，設計減少火炮發射沖擊的粘彈性膠泥減振器。