多種因素影響下鎢合金破片的穿甲深度研究

舒張憶南，梁爭峰，阮喜軍，何 勇

(西安近代化學研究所，西安 710065)

1 引言

防空反導導彈大多以破片殺傷戰斗部為主要毀傷元，通過裝藥爆炸來驅動產生的破片群，利用破片的動能來對目標進行侵徹毀傷。因此，評估破片殺傷戰斗部的毀傷威力的一個重要指標就是破片的穿甲深度，也就是在一定的參數下破片能貫穿多厚的裝甲防護。影響這個指標的因素有很多，包括破片的質量、形狀、著靶速度等等，研究這些參數對破片穿甲深度的影響具有重要意義，可以為戰斗部的設計提供參考。

在選擇材料時，鎢合金由于其具有密度大、存速能力好、穿透性強等一系列特點，在殺傷戰斗部破片材料中占據了很大一部分比重。許多研究者都對鎢制破片的性能進行了研究，唐嬌姣研究了鎢合金破片力學特性與爆轟驅動破碎行為的關聯性，用動態力學性能分析和金相研究結合預估了破片的爆轟驅動破碎行為；王祝波等利用數值模擬的方法研究了鎢破片形狀對穿甲速度的影響，得到了立方形破片速度、動能在穿甲過程中衰減最大的結論；趙小峰研究了破片質量對鎢合金破片侵徹威力的影響，通過理論計算、數值仿真和試驗驗證相結合，得出了隨著破片質量的增大，破片最大侵徹深度逐漸增加，但增大率減小的結論；譚多望等對球形鎢合金破片終點彈道性能進行了實驗研究，總結了鎢珠長距離飛行時的速度衰減規律并修正了侵徹靶板后剩余速度計算公式；弗勞恩霍夫實驗室的Patrick Frueh等人對含鈷和不含鈷2種不同成分的鎢合金破片的終點彈道性能進行了比較，發現鎢合金的成分對破片穿甲深度具有相當大的影響；土耳其TOBB大學的Hakan Hafizoglu等則考察了燒結溫度和Ni/Fe比對液相燒結鎢重合金破片彈道性能的影響，結果表明一定燒結溫度下的鎢合金破片穿孔性能最好，過高或過低的溫度都會影響穿甲能力。但是目前綜合考慮多種因素同時作用的情況，并且比較這些因素對穿甲深度的影響效果的研究者還比較少。

本文通過理論計算和利用LS-DYNA進行數值模擬計算的方法研究在質量、形狀和著靶速度等多種因素的共同影響下，鎢制(93 W)破片侵徹Q235裝甲鋼的穿甲深度變化情況，總結各因素對穿甲深度的影響規律，找出對穿甲深度影響較大的因素，修正穿甲深度的計算公式并通過靜爆實驗來驗證修正后的公式。

2 靜爆試驗

為了研究鎢合金破片的穿甲深度，設計了不同破片參數的殺傷戰斗部樣機，采用地面靜爆打靶試驗的手段，來獲取破片的穿甲深度參數。試驗現場布局如圖1所示。

在距爆心12 m處沿圓弧連續布設Q235鋼靶，高度為5.5 m，弧長為7.5 m，鋼靶由幾塊厚度分別為10 mm、12 mm、14 mm、16 mm等依次遞增的靶板組成。

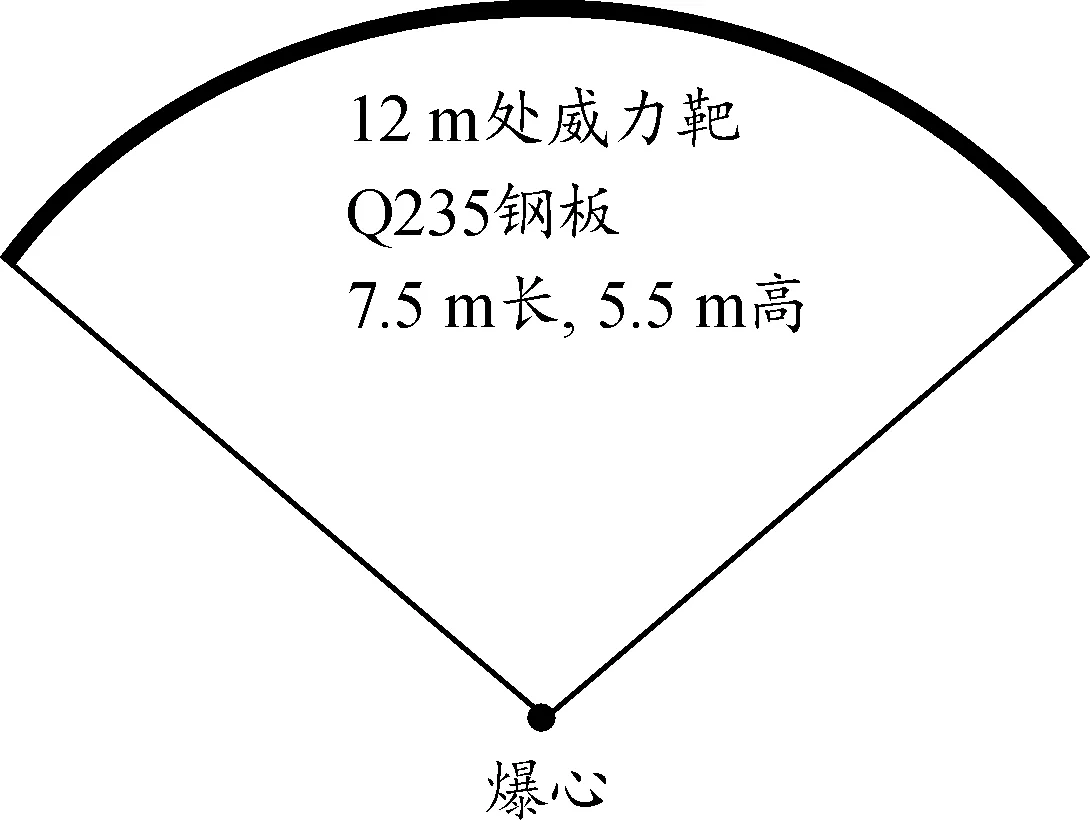
圖1 試驗現場布局示意圖

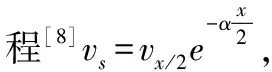
破片在靶板上的穿孔如圖2所示，收集了幾組不同情參數下的破片穿甲深度數據，靜爆試驗結果如表1所示。

圖2 靶板破片穿孔示意圖

表1 靜爆試驗結果Table 1 Static explosion test results

3 數值模擬計算

3.1 建立計算模型

因地面靜爆試驗只能得到有限幾種工況下的破片穿深數據，要進行深入研究，需要使用LS-DYNA軟件對鎢制破片在多種影響因素下的穿甲深度進行數值模擬仿真。

破片材料使用93W鎢合金，查閱文獻[9]可知其密度=17.6 g/cm，同時考慮到質量、形狀和著靶速度等因素，選擇的破片種類有9種，分別是直徑為Ф6.88 mm、Ф8.16 mm和Ф9.54 mm的鎢合金球，直徑為Ф4.77 mm、Ф5.66 mm和Ф6.61 mm，長徑比為2∶1的鎢合金圓柱，以及邊長分別為5.54 mm、6.57 mm和7.69 mm的鎢合金立方體，3種大小破片的質量分別約為3 g、5 g和8 g。這些破片分別以一定的著靶速度侵徹裝甲鋼靶板，著靶速度從1 000 m/s開始依次增加500 m/s直到3 000 m/s。裝甲鋼靶板的材料選擇Q235鋼，查閱文獻[10]后得到，Q235鋼的楊氏模量=200 GPa，泊松比=0.3，比熱容=469 W/(m·K)，密度=7 800 kg/m，熔化溫度=1 795 K。靶板采用半無限靶，邊長為100 mm，厚度為200 mm，考慮到破片尺寸與靶板尺寸相比為小量，靶板可以認為是無限區域，對靶板施加非反射邊界條件。由于模型具有軸對稱特性，為簡化計算可以取1/4模型，然后對1/4分割面上所有節點施加對稱面法相約束。破片和靶板均采用Lagrange算法，六面體網格劃分，計算模型如圖3所示。

圖3 數值仿真計算模型示意圖

破片和靶板在侵徹過程中互相擠鑿破壞，因此需要用面面沖蝕接觸(CESTS)來定義破片與靶板之間的接觸類型，并且由于這個過程伴隨著大變形、高應變率和高溫，需要用Johnson-Cook本構模型和Gruneisen狀態方程模型來描述破片和靶板。模型各參數如表2和表3所示。

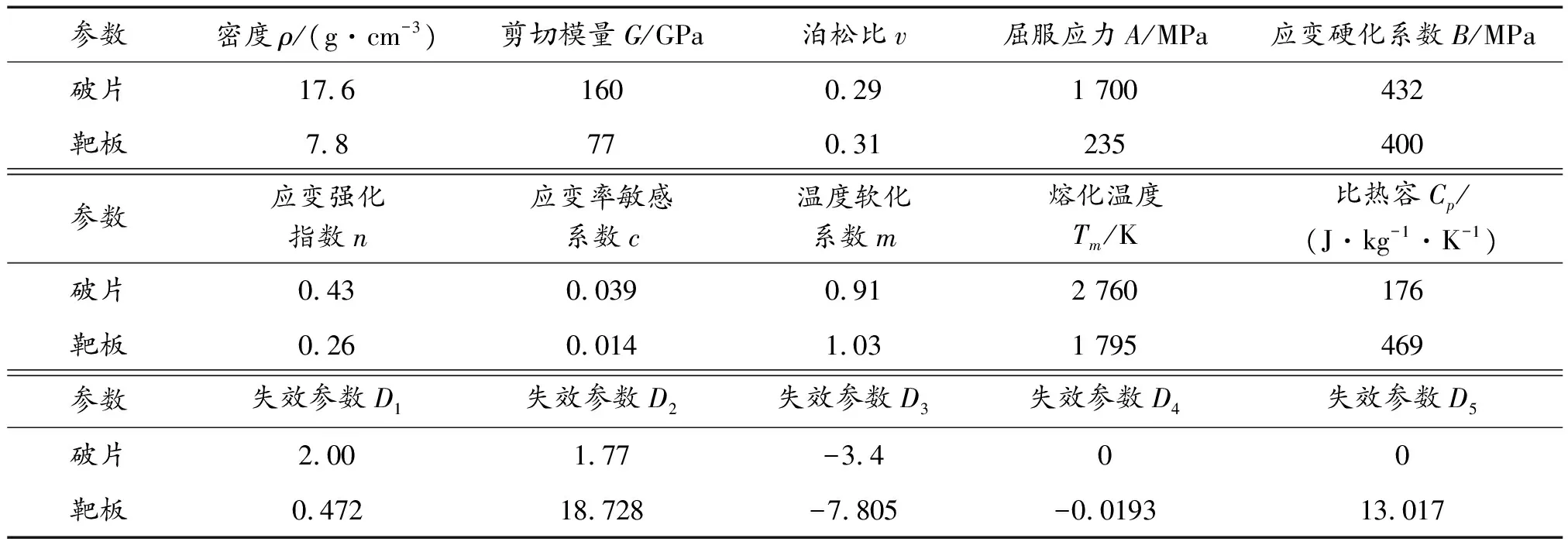
表2 Johnson-Cook本構模型相關參數Table 2 Related parameters of Johnson-Cook constitutive model

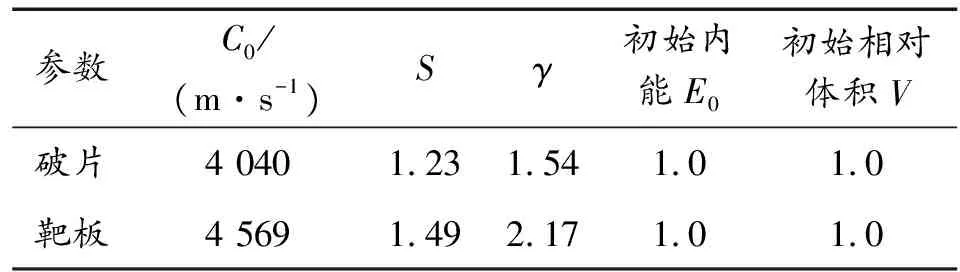
表3 Gruneisen狀態方程模型相關參數Table 3 Related parameters of Gruneisen equation of state model

3.2 計算結果分析

在數值模擬破片侵徹靶板的過程中，破片著靶后在慣性和靶板壓力的作用下發生沖蝕和塑性變形，逐漸扁平化，邊緣向外擴散并向上彎曲，著靶速度越大現象越明顯，高速時呈現一個中間凹陷四周向上蜷曲的狀態，過程中有一定的質量耗損，速度越大耗損越嚴重。同時靶板也發生沖蝕和塑性變形，形成一個尺寸隨深度而減小的穿孔，初始尺寸明顯大于破片著靶面積。3種破片著靶時和侵徹結束時的典型形態如圖4所示。

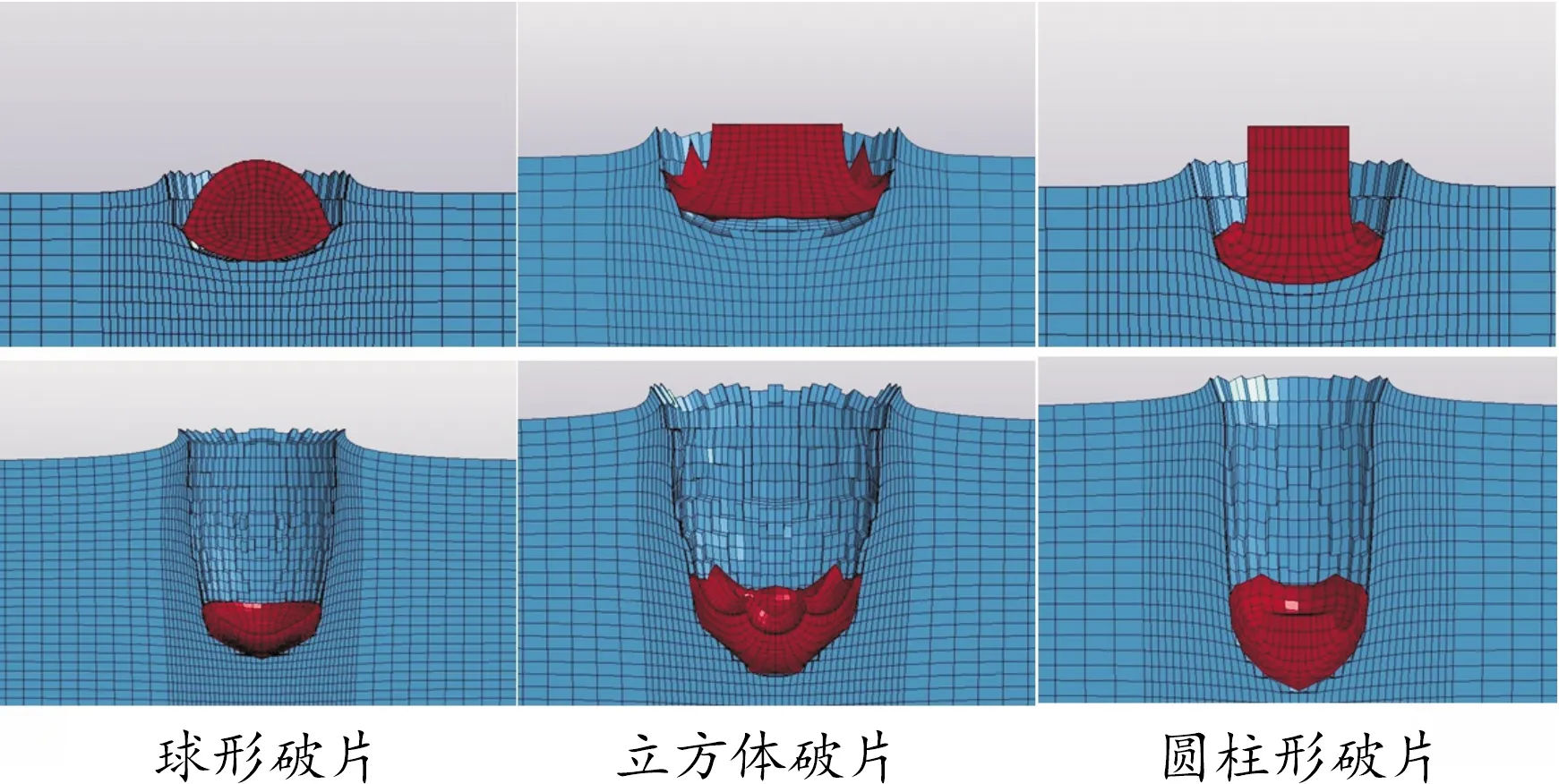
圖4 3種破片著靶時和侵徹結束時的典型形態示意圖

數值模擬計算得到的不同情況的穿甲深度如表4所示,根據表4分析可知，3種影響因素中，在其他條件相同的情況下改變破片形狀更容易對穿甲深度造成較大的影響，改變破片著靶速度次之，改變破片質量對穿甲深度的影響最小。破片穿甲能力主要取決于破片自身的動能大小，破片形狀主要影響了破片的著靶面積，著靶面積越小破片受到的阻力越小，因此動能損耗也小導致穿甲深度增大，如圖5所示，圓柱形破片速度損耗最小，因此同等條件下穿甲深度最大。而增大質量在動能提高的同時也增大了著靶面積，導致穿甲深度的增加不明顯，如圖6所示。

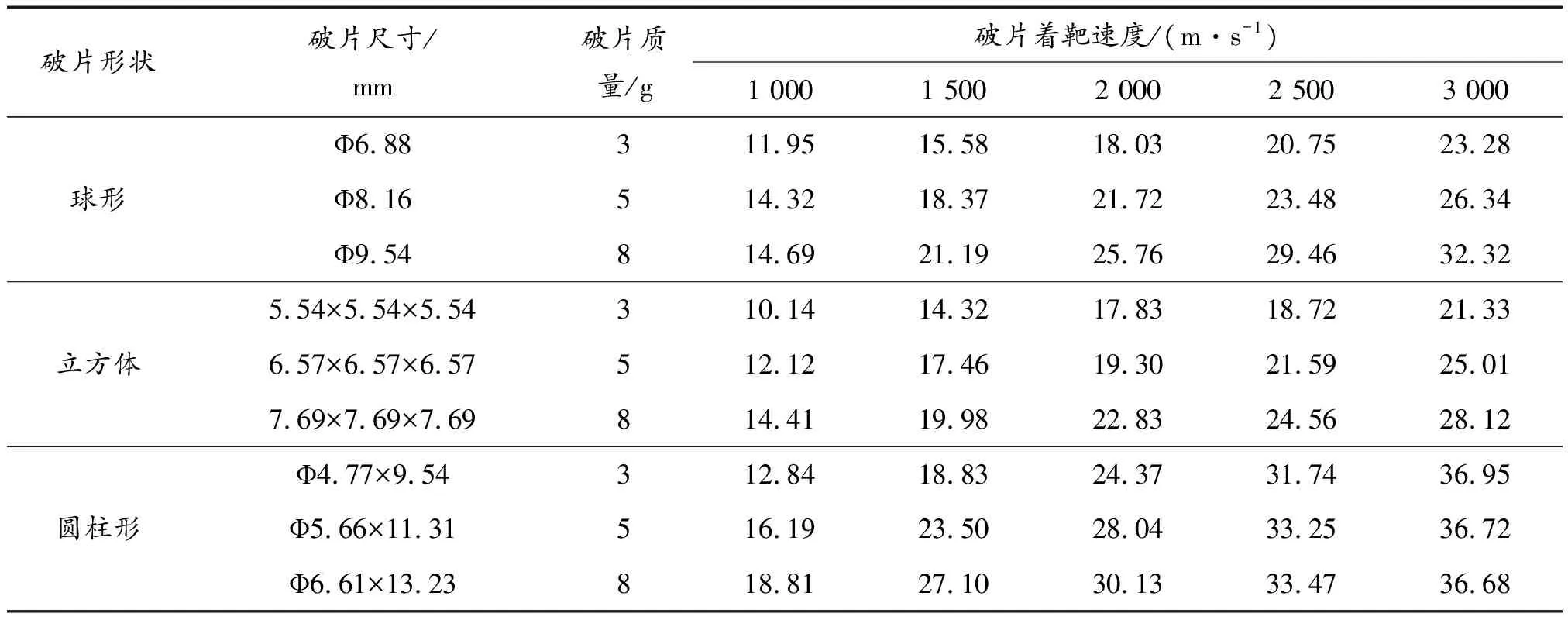
表4 破片穿甲深度仿真計算結果(mm)Table 4 Simulation results of fragment penetration depth

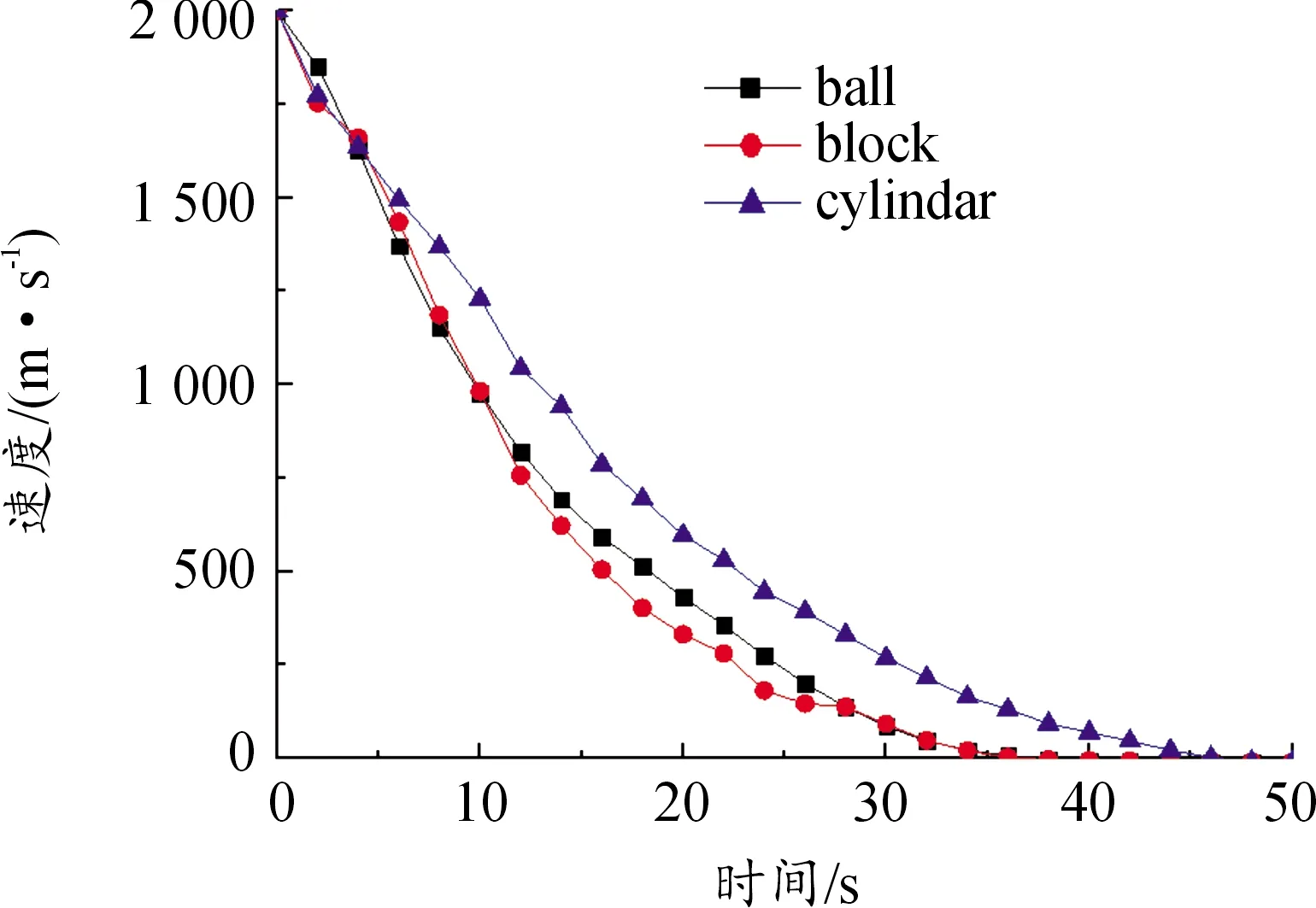
圖5 不同形狀的5 g破片在著靶速度為 2 000 m/s時的速度時程曲線

4 理論分析與計算

4.1 破片穿甲深度計算

破片穿甲深度的計算公式可以通過破片剩余速度公式推導得到，計算破片剩余速度通常采用基于大量實驗數據總結而成的THOR經驗公式，表達式如下：

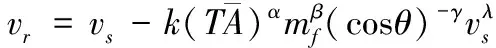
(1)

在不考慮著靶角度的影響時，破片均為正撞擊靶板的狀態，即=0。根據式(1)可以推導，當破片剩余速度=0時，此時的靶厚就是破片在著靶速度為和質量為的情況下的破片穿甲深度，表達式為

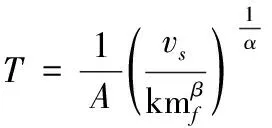
(2)

根據文獻[8]，低碳鋼靶板相關參數分別為=5 791 m/s、=0.906和=-0.963，代入式(2)可計算得到選擇的9種破片在1 000～3 000 m/s速度范圍內的破片穿甲深度。

4.2 計算結果及分析

根據式(2)得到了9種破片的穿甲深度，結果如表5所示。

與數值模擬計算的結果對比，理論計算得到的穿甲深度普遍較大，尤其是立方體和圓柱形這2種形狀的破片，這是由于理論計算公式中沒有考慮到破片的形變和侵徹過程中質量損耗對穿甲深度的影響。低速時球形破片形變不是十分明顯，由形變所導致的動能損耗較小，因此穿甲深度的數值模擬計算和理論計算結果相差較小，而立方體破片和圓柱形破片在侵徹過程中發生較大的形變，造成更大的動能損耗。高速時由于破片質量損耗嚴重，穿甲深度的數值模擬計算結果增幅變小，導致與理論計算結果相差巨大，理論計算公式結果不再適用。

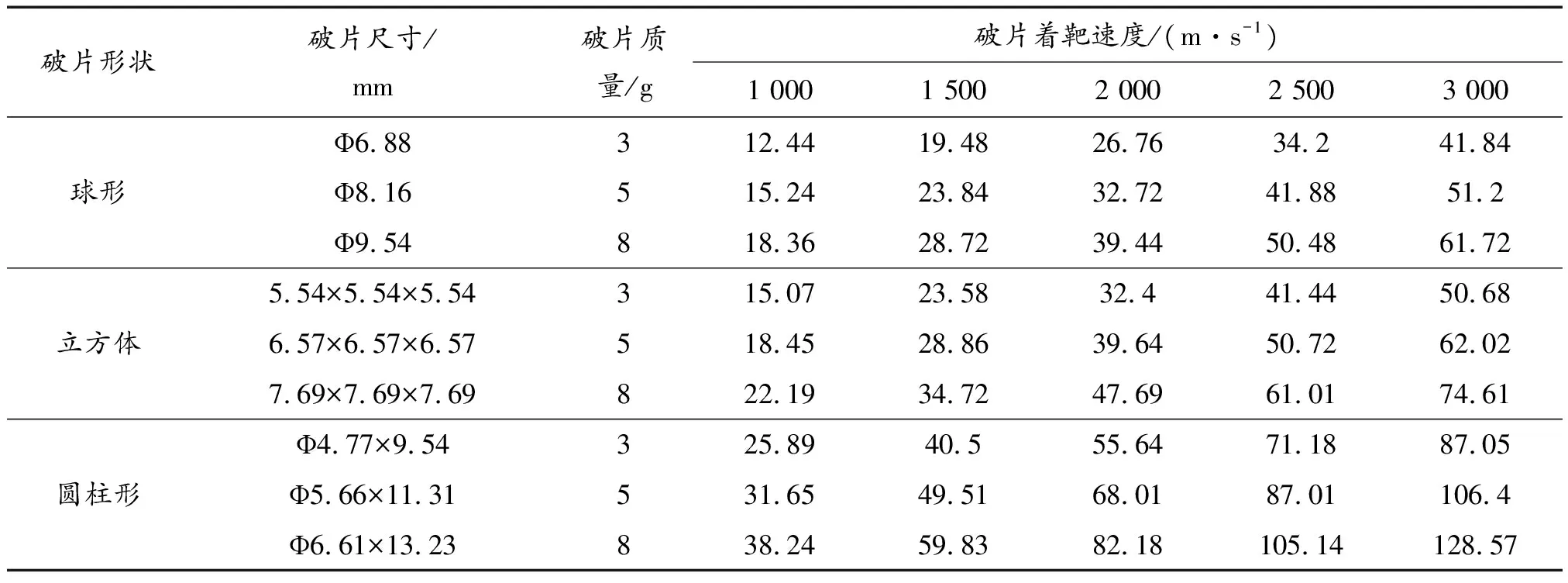
表5 破片穿甲深度理論計算結果(mm)Table 5 Theoretical calculation results of fragment penetration depth

4.3 理論計算公式修正

為了使理論計算的結果與數值模擬計算的結果符合，需要對破片穿甲深度的理論計算公式進行修正，添加形狀修正系數，改變速度和質量影響系數。修正后的計算公式形式如下：

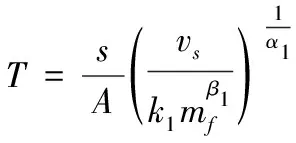
(3)

式(3)中：為形狀修正系數，、和分別為修正后的速度和質量影響系數，其他參數含義與式(1)、式(2)相同。

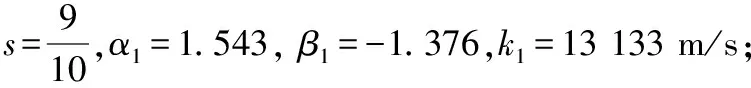
因此，修正后的93W鎢合金破片穿甲深度計算公式如下：

(4)

為了驗證修正后的理論計算公式的可靠性，將理論計算、數值模擬仿真和靜爆實驗的結果進行對比，如表6所示。結果表明除了一組數據之外其他數據的誤差都在5%之內，證明了數值模擬和修正后的理論計算公式的有效性。

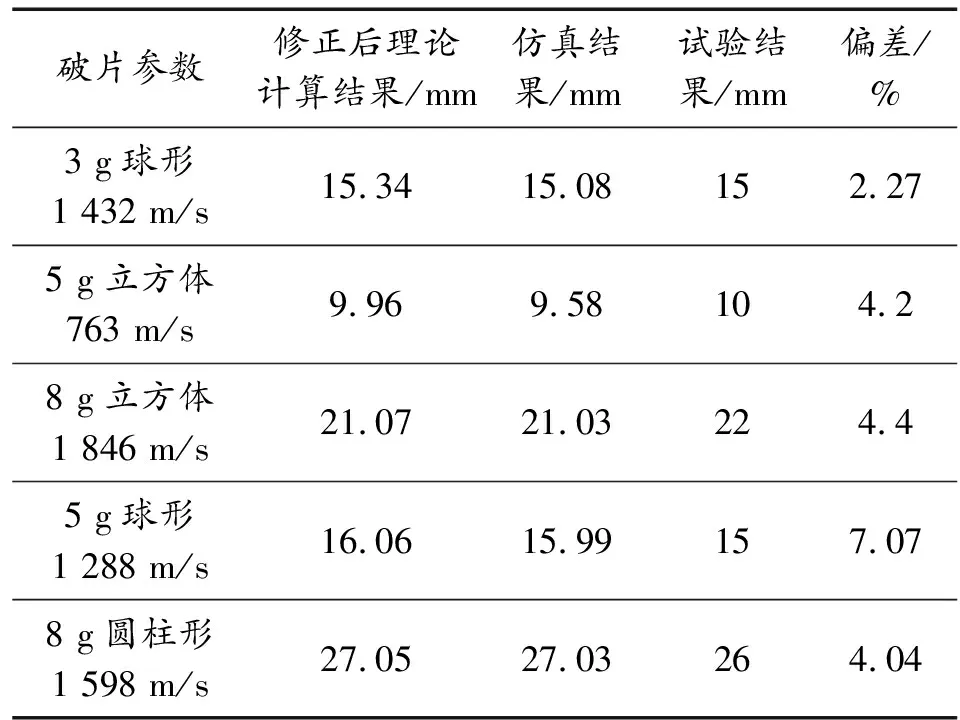
表6 試驗結果及比對Table 6 Test results and comparison

5 結論

1) 鎢合金破片侵徹Q235鋼靶時，用改變破片形狀的方法來增大破片的穿甲能力是最容易且有效的。在破片質量和著靶速度都相同時，長徑比為2∶1的圓柱形破片穿甲深度平均是立方體破片的1.3～1.5倍，在高速情況下差距更為明顯。如果無法保證圓柱形破片合適的著靶角度，破片的穿甲能力會大幅降低，所以仍然推薦使用穿甲能力穩定的球形破片。

2) 破片質量和著靶速度比較，按相同比例增大破片著靶速度可以更為有效地增加破片的穿甲深度。