一種巖石薄片離焦模糊圖像自動篩選方法

戴萬富， 滕奇志， 何海波， 劉豫璋， 張豫堃

（1 四川大學 電子信息學院， 成都 610065； 2 成都西圖科技有限公司， 成都 610014）

0 引 言

在巖石薄片的全幅面偏光圖像采集中，由于薄片本身的不平整性、系統硬件的不穩定性或者自動聚焦算法的局限性，部分視域采集的圖像會存在離焦模糊的現象，影響科研人員對巖石薄片性質的進一步觀察研究。 因此，需要將這些模糊的圖像篩選出來，再做進一步處理。 傳統方法是通過人工瀏覽所有采集的圖像，從中篩選出模糊的視域，由于顯微鏡下一張薄片往往會采集幾百甚至上千張圖像，人工方法費時費力，因此巖石薄片全幅面采集圖像的自動模糊檢測具有重要實際意義。

對于模糊檢測，學者們主要從圖像清晰度評價和局部模糊區域分割兩個方面進行了研究。 圖像清晰度評價通常是對整幅圖像進行質量評價以得到一個分值，該分值代表了人眼的銳度感知情況。 如，謝小甫、王紅玉、Wang 等將再模糊后的圖像和原圖 的 結 構 相 似 度 作 為 模 糊 評 價 值； Ferzli、Narverkar等則從邊緣擴散程度，衡量模糊評價值；Vu 等將變換域的頻譜、能量等作為模糊評價指標。 該類模糊評價方法通常對于全局模糊具有較好的效果，但對于存在局部模糊的自然圖像則效果不佳。 對于圖像的模糊區域分割，主要是對圖像中所有像素進行分類，以檢測出圖像中的模糊區域。 如，Xin等采用局部二值模式和一種穩定的分割算法來分割模糊區域；Alireza、Ma、Xiao等則從變換域角度分析局部的模糊情況，再采用封閉式摳圖算法得到圖像的模糊區域；Karaali 等先在圖像邊緣進行模糊分析，然后采用引導濾波擴散到整幅圖像，以得到模糊區域。 該類模糊分割方法往往假定圖像中只存在局部模糊，因此對全局模糊圖像效果較差。

由于巖石薄片采集的圖像中既可能存在全局模糊圖像也可能存在局部模糊圖像，因此本文方法借鑒上述兩類研究思想，先分塊對圖像進行模糊評價得到模糊度圖，然后由模糊度圖的統計特性，來整體劃分圖像為清晰、局部模糊或全局模糊，以此篩選出存在模糊的視域，同時該模糊度圖還可直接用于模糊區域分割。

1 本文方法

1.1 巖石薄片偏光特性的目標區域提取

巖石薄片采集的若干圖像中，在一部分視域內會同時存在標本和背景。 為了避免背景區域的干擾，有必要先提取出圖像中的標本目標區域。 在偏光顯微鏡中，巖石薄片的分析會從單偏光和正交偏光兩個方面進行。 正交偏光下背景區域呈黑色，標本區域的顏色則隨著礦物顆粒和偏光角度的不同而不同；而單片光下整個視域呈亮色，如圖1 所示，圖1 中第一行左上角為背景區域。 因此，在正交偏光下可以直接通過亮度閾值來得到目標區域，而對于單偏光圖像，可以綜合正交偏光多角度的掩膜，將其求并集即可。

式中，表示圖像的亮度；表示正交偏光二值化的閾值（本文通過對大量背景區域的亮度統計，并考慮到人眼對亮度的感知情況，取20）；表示正交偏光的二值化掩膜；表示在正交偏光角度為時的圖像掩膜；表示單偏光的掩膜。

圖1 第二行顯示了對一個位置各角度提取目標區域的結果。 從圖中可見，單一正交偏光圖像得到的掩膜難以完全表述單偏光下的目標區域，綜合多個角度的正交偏光掩膜可以準確表述單偏光下的目標區域。

圖1 目標區域提取Fig. 1 Target area extraction

1.2 圖像模糊與再模糊理論

圖像的模糊可以看成原始圖像與一個點擴散函數的卷積，在實際中，離焦模糊通常把建模為高斯函數，即：

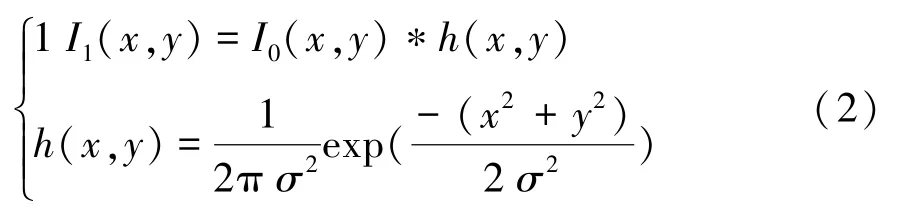
式中，表示模糊圖像；表示原始未失真圖像；表示高斯函數的標準差。

研究表明，對一幅清晰的圖像進行模糊，比對一幅已經模糊的圖像進行再次模糊所損失的信息要多。 如圖2 所示，第一行為模糊程度逐漸加深的失真圖像，第二行分別為第一行進行相同高斯再模糊所得到的圖像。 由此可見，對于第一幅較為清晰的圖像，其再模糊圖像與原圖像存在較大的不同，而對于最后一幅較為模糊的圖像，其再模糊圖像與原圖像幾乎看不出變化。 為定量衡量這種差異，本文計算了再模糊圖與原圖的均方誤差（Mean Squared Error，MSE）值，用以衡量原圖像與再模糊圖像的誤差大小。 其計算公式如下：

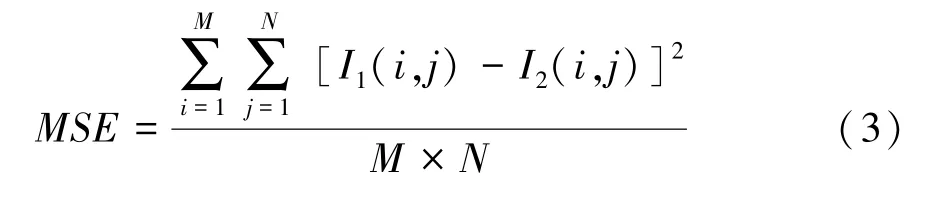
其中，、分別表示圖像的高和寬；表示原圖像；表示再模糊圖像。

從結果可見，若原圖像越清晰，則再模糊前后的值越大，圖像損失細節越多，而原圖像越模糊，則再模糊前后的值較小，圖像變化不大。 基于此，對于一幅待測圖像，可以通過再模糊構造參考圖像，由再模糊圖像與原圖像的差異來判斷待測圖像的模糊程度。

圖2 圖像再模糊Fig. 2 Image re-blur

1.3 空間域評價指標

值雖然可以反映出圖像再模糊前后的差異，但其受圖像內容影響較大，不能直接用于模糊評價中。 考慮到圖像的失真會導致梯度幅度的衰減，即梯度幅度的變化可以反映圖像的失真程度。 因此， Xue 等將梯度幅值相似度（ Gradient Magnitude Similarity， GMS）應用于有參考圖像質量評價中，并取得了較好的效果。 本文將引入無參考模糊評價中，先通過對待評價圖像做高斯再模糊構造參考圖像，利用和的來衡量圖像的模糊程度。計算方法如式（4）所示，

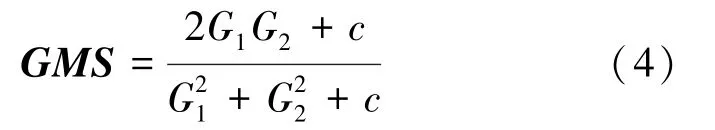
式中，是一個小的正常數用于避免分母為0，和分別表示失真圖像和再模糊圖像的梯度幅值圖。 由于Sobel 算子對噪聲具有較好的抑制作用，因此本文使用Sobel 算子來計算圖像梯度。

逐像素計算原圖與再模糊圖的值，即可得到一幅圖像的矩陣。 圖3 顯示了清晰圖像與模糊圖像在矩陣上的差異，其中第一行表示清晰圖像，第二行表示模糊圖像，列是由列經3 的高斯濾波得到的再模糊圖像。 比較、列梯度圖可見，清晰圖像再模糊前后其梯度幅值變化較大，而模糊圖像的梯度幅值變化則較小，因此列中清晰圖像矩陣的灰度值比模糊圖像更低。

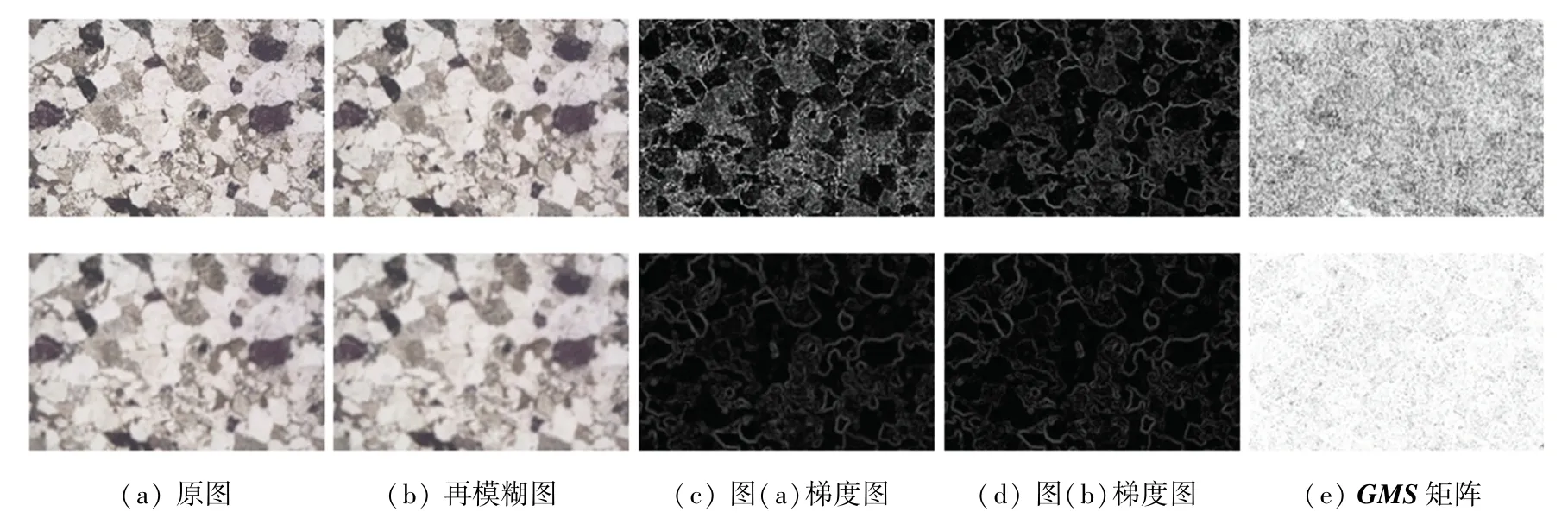
圖3 清晰圖像與模糊圖像GMS 的比較Fig. 3 Comparison ofGMS between clear image and fuzzy image

為了定量衡量圖像模糊程度與的關系，定義大小矩陣均值為空間域的模糊評價指標：

由以上分析可知，圖像越模糊，其再模糊圖梯度幅值變化越大，值越接近于1；反之，圖像越清晰，值越接近于0。 因此，可以從空間域角度有效衡量圖像模糊程度。

1.4 頻率域評價指標

圖像的模糊在空間域體現為梯度的衰減，在頻率域則體現為高頻系數的減少。 考慮到離散余弦變換（Discrete Cosine Transform， DCT）對能量具有較好的集中性，對圖像模糊具有更好的響應，并且計算復雜度較低，因此本文從變換角度構造頻率域評價指標。

對于的圖像，其二維變換如下：

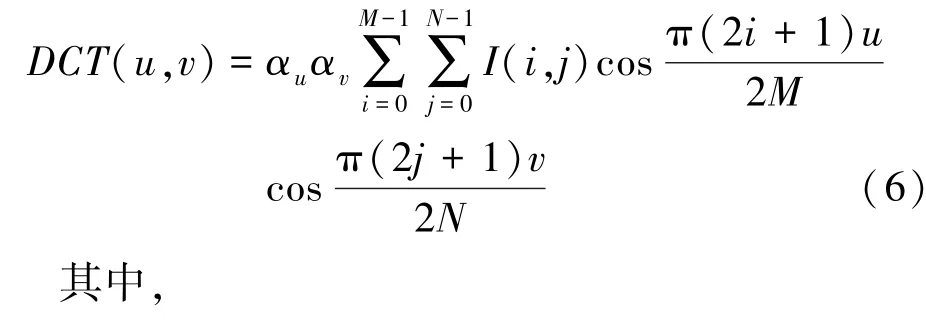
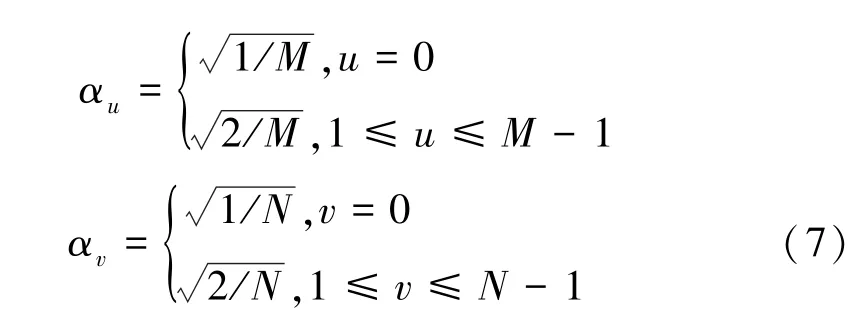
圖4 顯示了清晰圖像與模糊圖像在系數上的差異，第一行表示清晰圖像，第二行表示模糊圖像。 其中列是由列經3 的高斯低通濾波得到的再模糊圖像，圖、列分別表示其圖。 比較、列可見，清晰圖像經再模糊后損失大量高頻系數，而模糊圖像經再模糊后其系數變化較少，因此再模糊前后系數的變化可以有效衡量圖像的模糊程度。

圖4 清晰圖像與模糊圖像的DCT 系數比較Fig. 4 Comparison ofDCT between clear image and fuzzy image

為了定量衡量圖像模糊與系數的變化關系，頻率域的模糊評價指標定義如下：

由上述分析可知，圖像越模糊，再模糊前后系數差異越小，值越接近于1；反之，圖像越清晰，值越接近于0。 因此，值可以從頻率域角度有效衡量圖像的模糊程度。

1.5 分塊評價圖像模糊程度

僅僅從空間域或者頻率域難以準確衡量圖像的模糊程度，本文綜合空間域和頻率域方法，定義其加權和作為模糊評價值：

其中，0 ≤≤1（本文中取0.5 時效果最佳），S表示對圖像塊的模糊評分值。

在顯微鏡采集的圖像中，即存在因為聚焦失敗導致的全局離焦模糊，也有因為景深不夠而導致的局部離焦模糊，若直接對整幅圖像進行評價，則局部模糊圖像會受到清晰區域的影響而產生錯誤結果，因此需要對圖像進行分塊處理。 同時，考慮到多尺度在模糊評價中的廣泛應用，小尺度塊對邊緣具有較好的保留效果，但在灰度平坦區域易產生誤判；而大尺度塊雖然對邊緣有一定平滑，但其對灰度平坦區域響應較好。 本文綜合多尺度的影響，采用滑動窗口機制，在每個窗口上取大小為16、32、64 3 種大小的尺度塊，最后采用加權求和的方式得到每個窗口位置的最終評分值：

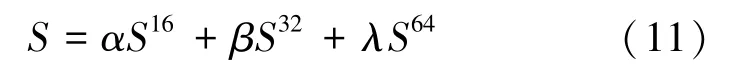
其中，、、表示各尺度塊的權重，且1。 考慮到巖石薄片顯微圖像中灰度平坦區較多，因此本文取∶∶2 ∶3 ∶5。的最終取值范圍為0～1。越接近0，圖像塊越清晰，越接近1，圖像塊越模糊。 求得所有窗口的分值，即得到圖像的模糊度圖。

圖5 顯示了清晰、全局模糊、局部模糊的薄片圖像以及其所對應的模糊度圖，圖、中紅色框大致標出了局部模糊所在的區域。 從圖中可以看出，清晰圖像所在區域的分值較低，而模糊區域的分值較高；從圖、和中還可以看出，圖像中背景區域與模糊區域呈現相近的模糊程度，因此有必要排除背景區域以得到正確的目標區域模糊分布情況。

圖5 清晰、局部模糊和全局模糊圖像的模糊度圖Fig. 5 Fuzziness map of clear， locally blurred and globally blurred images

為了將圖像分類為清晰、全局模糊和局部模糊，本文計算了模糊度圖中目標區域的標準差σ和均值μ。 可以預見的是，局部模糊圖像中模糊度分布不均勻，其應具有較大的標準差，而清晰和全局模糊圖標準差相對較小，但清晰圖像應具有更低的均值。因此可以通過標準差閾值σ和均值閾值μ來判斷圖像類別。 若σ＞σ，則圖像為局部模糊，否則繼續判斷均值；若μ＜μ，則圖像為清晰，否則μ＞μ，為全局模糊圖像。 圖5 展示了部分圖像的標準差和均值，本文通過實驗，驗證了σ的合適值為0.06，而μ的合適值為0.72。

2 實驗結果分析

2.1 模糊圖像篩選

本文實驗數據由課題組“巖石薄片偏光采集系統”采集所得，從中隨機選擇不同薄片部分圖像用于驗證本文算法。 其中包括清晰圖像126 幅，局部模糊圖像109 幅，全局模糊圖像86 幅，共321 幅巖石薄片圖像。 提前標記好圖像真實類別，然后用本文算法預測其類別。 在統計分類任務中，常采用準確 率（）、 精 確 率（） 和 召 回 率（） 來對算法進行評估。

其中，準確率衡量算法的整體性能，精確率衡量算法檢測的準確性，而召回率則衡量算法檢測的全面性。 其計算方式如下：

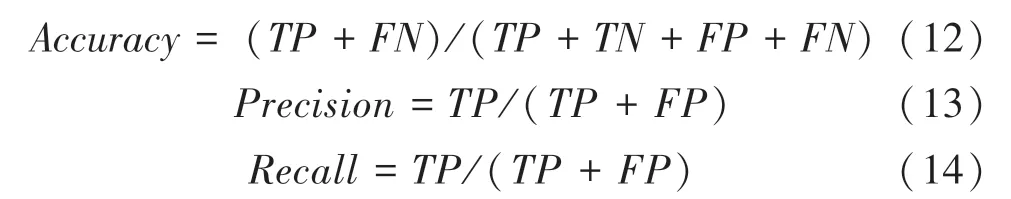
式中，表示真正例，即正類中正確預測的樣本；表示假反例，即正類中被錯誤預測為反類的樣本；表示真反例，即反類中正確預測的樣本；表示假正例，即反類中被錯誤預測為正的樣本。 對321 幅樣本圖像進行預測，得到其混淆矩陣見表1。

表1 三分類混淆矩陣表Tab. 1 Confusion matrix table with three class

表中橫軸表示預測值，縱軸表示真實值。 從混淆矩陣中可以看出，在所有圖像上的準確率達到93.15%，清晰、局部模糊和全局模糊各自分類的精確率分別為90.97%、93.45%、96.29%，召回率分別為96.03%、91.74%、9.69%，平均精確率達到93.57%，平均召回率達到92.82%。 算法在具有較高精確率的同時也能保持較高的召回率，說明對模糊圖像具有較好的分類能力。 在算法完成分類預測后，全局模糊圖像和存在局部模糊的圖像即為所要篩選的離焦模糊圖像。

2.2 局部模糊區域檢測

在巖石薄片圖像采集中，全局模糊一般是由于自動聚焦失敗而導致，對于此類圖像只需回到相應位置重新對焦采集即可；而局部模糊圖像一般是由于成像系統景深不夠導致，對于此類圖像則需要進行再處理，如采用去模糊算法或多聚焦圖像融合等算法。 由上述分析可知，在算法得到的模糊程度圖中，模糊區域具有較高的評價值，清晰區域具有較低的評價值，因此直接在模糊度圖上采用自適應二值法即可提取圖像的模糊區域。 將本文提取的模糊區域與其它算法進行比較，部分結果如圖6 所示。 其中，第一列圖片中的紅色方框大致標出了模糊區域，圖中灰色區域表示通過正交偏光特性提取出的背景區域，白色區域表示分割的模糊區域。 從圖中可以看出，本文算法在提取模糊區域時具有更好的連續性，不易受平坦區域影響而產生誤判，具有更高的準確性。

圖6 模糊區域分割效果對比Fig. 6 Comparison of Fuzzy area segmentation

3 結束語

本文提出的針對巖石薄片顯微圖像的自動模糊檢測算法，首先通過巖石薄片的偏光特性提取圖像中目標區域，然后對目標區域進行再模糊，并結合空間域和頻率域方法對在模糊前后的差異進行考量，以衡量圖像局部區域的模糊程度，最后采用模糊度圖的統計特性來將圖像分類為清晰、局部模糊和全局模糊。 實驗結果證明，該方法可以從巖石薄片采集的大量圖像中有效篩選出模糊圖像，并且也能對圖像中的模糊區域進行分割便于對其再處理，具有一定的實用性。