錯出來的精彩

親愛的讀者朋友，請看一道去年某小學畢業(yè)測試卷的“壓軸題”（如圖1）。建議您閱讀全文前，先用幾分鐘時間“下水”試一試。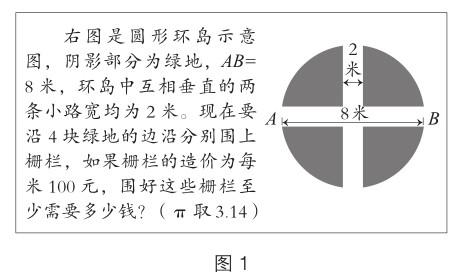

您的答案是多少？是不是4284元？

今年總復習時，我讓學生練習這道題，班級正確率高達90%，挺令人滿意的結果。但班內公認的“數學大咖”王睿沒得分，原本“正確”的解答被他劃去了，讓人頗為意外和不解。憑他的實力，不應該有困難的。因此，評講這道題時，我特意讓他來說說想法。

王睿站起來就說：“這是一道錯題，根本沒法做。”

“錯題？”我和其他學生都有點懵。

他舉起他的答卷指給我看。我這才注意到，他的答卷上其實保留了一個示意圖（如圖2）。見我還是沒明白，他一邊指著弧線的拼接處，一邊自信地說：“這兒的‘彎度變了，這四塊陰影拼出來的根本就不是一個圓！”他這么一說，我終于明白了示意圖的意思，心想：“完了完了，攤上事了！”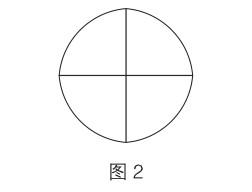

臺下的學生依然一頭霧水。

王睿更來勁了，沒等我發(fā)話，就直接踏上講臺，連講帶寫地開始了他的陳述：“你們的做法是不是把四塊陰影往中間一擠、一拼，然后求出這個半徑為3米的圓的周長，再加上8條3米的半徑，就以為求出了陰影的周長？”

“是啊！”多數人都是這么想的，也有少數學生說是先算出一個90°扇形的周長，再乘4，求出陰影部分的總周長，進而求出需要的錢數。

“你們的方法，都犯了一個同樣的錯誤，那就是四塊陰影往中間一壓，得到的并不是一個標準的圓，而是一個不方不圓的圖形。”王睿看著大家不解的眼神，迅速用投影展示了他的示意圖。接著，拿筆在兩段弧線的拼接處反復勾畫，強調那兒的“曲度”發(fā)生了改變。

教室里一片安靜。

但真正緊張的還是我——我選了一道“錯題”讓學生做！去年那么多學生做了這道題，那么多老師講評了這道題！怎么收場？

是表揚王睿“真厲害”，還是說“錯題就不管了”？是努力摳摳字眼維護命題老師和我的權威，還是把題改得嚴謹一些再做一次？

好像都不合適。

平時工作中，這樣的“差錯”并不少見，比如看錯、算錯。每當發(fā)生這種情況，往往是教師的一句“搞錯了”后，學生就用大度的笑聲化解尷尬。但今天是我和命題老師都“想錯”了，還能回避嗎？

華應龍老師說過：“人生自古誰無錯？錯若化開，成長自來。”我們應主動接納“差錯”，并努力將這些“差錯”轉化為學習資源，進而“化錯養(yǎng)正”。

冷靜下來的我，決定試著請學生來“化”這個“錯”。

“同學們，這真不是老師故意設置的陷阱！去年六年級的學生和老師，包括命題的老師都掉進去了，說明這道題值得我們好好討論。而且能發(fā)現它有問題，說明你們很厲害啊！”我的坦誠，獲得了學生的認可。于是，我把話語權徹底交給了學生：“關于這道題，我們最應討論哪些方面？”一番交流，大家認為“老師為什么會出錯？”和“遇上這樣的錯題該怎么辦？”這兩個問題應好好討論。雖然我心里沒底，還是點頭同意了。經過幾分鐘的獨立思考和組內交流，開始了全班分享。

首先，交流問題“老師為什么會出錯”。同為“數學大咖”的李思遠邊畫示意圖（如圖3）邊說：“老師，我知道命題老師為什么會出這樣的錯了，他應該是受了這道題的影響。”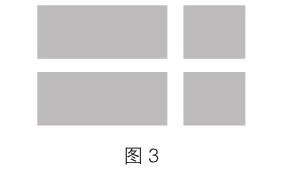

李思遠一手指著他畫的示意圖，一手舉起試卷，接著說道：“命題老師應該是覺得這道題中的圓也可以像長方形一樣，往中間一壓就會組成一個新的圓。但環(huán)島是一個圓，鋪了兩條小路后，圓周就只剩下4條曲線了。曲線的彎曲度并不會因為鋪路而改變，對應的半徑還是原來的4米，而不是現在看到的3米，也就是說，以圖中的直角頂點為圓心，以3米為半徑畫出的弧線不是這樣的。因此，這四塊陰影是拼不成一個圓的，我們也不能用3米為半徑來計算曲線的長。”

李思遠的思路很清晰，但多數學生還是迷茫地看著他。

發(fā)現臺下的學生還是不明白，他在黑板上又畫了一個示意圖（如圖4），邊指邊說：“這段曲線對應的半徑是虛線標出的這兩段，而不是實線表示的這兩段，而這樣的四段曲線拼出來的，就是王睿剛才畫的那個有點畸形的圓。”

教室里響起了掌聲，看來，大部分學生明白了“拼不成”的原因。

我及時小結：“看來，經驗是我們解決新問題的好幫手，但有時候也會幫倒忙。對待新問題，我們需要思考得更細一些。如果時間充足的話，也可以動手驗證驗證，動手又動腦，才能有創(chuàng)造！”學生紛紛點頭。看來，大家都體會到了“錯題”的價值。

“老師，我突然覺得這道題不一定錯了呢！”王睿語出驚人，“拼接后肯定不能當成一個標準圓來算，但我們可以不拼啊。我們可以先算出半徑是4米的圓的周長，再減去4段“路口”小曲線的長。每段小曲線的長度不好算，但與路寬2米的差距也就一點點，我們可以當作2米，題目中問的是‘至少要多少錢，至少就可以是近似數吧。”

教室里瞬間就炸鍋了，“就是，近似！”“只要差得不多就行了！”“這不算是錯題！”

這其實也是我意識到這道題有問題時，想到的應對辦法之一，現在由學生自己提出來，真好。我做出為難的樣子問道：“那這道題究竟是不是錯的？”

“我覺得這道題沒錯，但不是近不近似的原因。”一直沒發(fā)言的沈思竹說道，“大家現在都理解為是在半徑為4米的圓形環(huán)島中鋪了兩條路，所以剩下的部分拼不成一個圓。但也可能本身就是一個半徑為3米的圓形綠地，先分成四個扇形，然后再用這四個扇形鋪成的這個環(huán)島，所以，這道題沒錯啊。”

學生紛紛點頭，再次認為這道題沒錯。

這個答案也完全在我預料中。我微笑著說：“解鈴還須系鈴人，正解得問出題人。究竟是什么意思，還是問問出題老師吧？”

我的話音剛落，就有學生插嘴道：“不用問，就是錯的！第一句話就說了，這是一個‘圓形的環(huán)島。”

這下鐵證如山了，“圓中鋪路”，這果然是一道“錯題”。

“其實，這樣的‘錯題平時也不少啊。特別是那些判斷題，好多毛病哦！我覺得老師應該給我們說理由的機會。比如‘圓的半徑都一樣長這道題，如果都不是同一個圓，還有比較的必要嗎？就像我問你‘正方形的四條邊一樣長，算對還是錯呢？要是我當老師，一定不出這樣的題去為難學生，只要他真正明白道理就行了。”李思遠思考得果然很遠。

聽聽學生的“真心話”，做一個安靜的欣賞者，真好。

見時機已成熟，我問學生：“各位同學，我們花了這么多時間，討論這道‘錯題，到底有沒有意義呢？”

“有意義，其實剛才沈思竹都已經幫出題老師改掉了，就改成‘這是4個半徑為3米的90°扇形組成的環(huán)島就行了，改后的題還是很有挑戰(zhàn)性的。”張智明很肯定地說。

“我也覺得很有意義。如果是在生活中解決真實問題，就算不改題，也是可以通過近似計算來處理的——先算出大圓的周長，再減去4個缺口，每個缺口算作2米。但考試時、學習時可不行，數學必須嚴謹，當成圓來算，是對題意的理解有誤。”沈思竹簡直就是我的代言人。

“那考試時遇到這樣的問題，我們究竟應該怎么做呢？”我接過話題，對學生進行“靈魂拷問”。

“當然要做啊，萬一是我們自己想偏了，豈不是白白丟分。只是，如果覺得題目有問題，我們可以在下面寫上我們的疑問，說不準老師還會給附加分呢！”張智明的回答獲得一片掌聲。我也適時補充道：“是的，出錯題、做錯題都不可怕，可怕的是輕易放棄，不去反思錯因。”

后來的課堂，還談到了“按原題的表述有沒有辦法計算出準確的結果？”“當成圓來算與精確結果之間有多大的差距？”“圖中標注大圓的直徑8米是不是規(guī)范？”“題目中的圖是不是誤導了我們？”等問題。

事情已過去快一個月了，一些細節(jié)已開始變得模糊。但每每回味，總會有新的體悟和想法，我對“化錯”的感悟也愈加深刻。

平等的課堂最精彩。這是一堂充滿意外的課，卻無比精彩。究其原因，一定程度上緣于這道“錯題”（實則是一道超出小學生知識范圍的題，利用勾股定理和三角函數可求解，學生最初的答案應算作錯解）。因為是“錯題”，學生就有了敢于“冒犯”教師的勇氣；因為是“錯題”，教師就少了“聽我講”的霸氣。“錯題”，客觀上促成了課堂的平等。

講理的課堂最精彩。因為教師“講理”，學生才能充分地“講理”，最終，讓教師和學生看到課堂的精彩。

“化錯”的課堂最精彩。我們不僅要鼓勵學生勇敢地站起來、勇敢地說出來，更應多一些“化差錯為資源”的大氣，自覺地“化錯為正”，讓學生更多一份質疑的勇氣。

不論誰的“錯”，皆可“化”出精彩。

（沈勇，特級教師，四川大學附屬實驗小學，郵編：610047）