一種改進的和/差波束的米波雷達低仰角目標DOA估計方法

胡 敏 陳伯孝 徐賽琴

(1.航天南湖電子信息技術股份有限公司 湖北荊州 434000；2.西安電子科技大學 西安 710071)

0 引言

米波雷達波長較長，波束寬且陣列孔徑受限，因此在低仰角條件下，陣列接收信號不僅包含直達信號，而且包含復雜的多徑信號。直達信號和多徑信號在雷達接收端產生嚴重的干涉現象，導致雷達難以對低空目標的仰角進行精準探測與跟蹤。低空測角的主要難題包括：一是對于低仰角目標，直達波和多徑散射回波通常處于一個波束寬度內，直達波和多徑回波的波程差較小，難以從時域、頻域和空域對直達波和多徑信號進行分辨；二是直達信號與多徑信號為空間臨近相干源，且受實際陣地地形的影響，復雜多變的多徑信號疊加在直達波信號上，直接導致陣列接收信號產生嚴重的幅相特征畸變現象，現有的解相干類超分辨算法難以獲得準確的信號子空間和噪聲子空間；三是現有的超分辨算法均基于理想遠場平面波模型，而實際的回波信號不僅有直達信號，更包含復雜的反射信號和散射信號，遠場平面波模型難以準確描述實際回波信號，信號模型失配問題極大降低了現有超分辨算法性能[6-9]。

目前，超分辨算法主要包括特征子空間類超分辨算法和最大似然算法(Maximum Likelihood，ML)[10]。代表性的特征子空間類超分辨算法有多重信號分類算法[8](Multiple Signal Classification，MUSIC)和旋轉空間不變算法[11](Estimation of Signal Parameters via Rotation Invariance Technique，ESPRIT)。MUSIC算法的基本思想是對陣列輸出數據的協方差矩陣進行特征分解，得到與信號子空間正交的噪聲子空間，利用信號子空間和噪聲子空間的正交性實現目標仰角估計。特別地，對于相干源，通過空間平滑的方法，恢復接收數據協方差矩陣的秩，實現目標角度的超分辨估計，即空間平滑MUSIC算法(Spatial Smoothing MUSIC, SSMUSIC)。由于空間平滑方法需要對陣列劃分子陣，陣列有效孔徑會有一定的損失。ESPRIT算法實現解相干處理的原理是利用子陣間的旋轉不變特性，通過估計子陣間的信號子空間，求解旋轉不變等式，實現陣列的DOA估計。ML算法利用陣列輸出信號的統計分布特征，將接收數據協方差矩陣投影到期望信號空間，實現目標仰角的最大似然估計。當信源數較多時，多維搜索的ML算法具有較大的計算量。通常，采用交替投影最大似然算法(Alternating Projection ML, APML)[13]代替最大似然估計算法，APML算法將多維參數估計問題轉化成一維參數估計問題，每次迭代優化過程中僅對眾多參數中的一個參數進行優化，極大減小最大似然算法的運算量。然而，這些算法在信號模型匹配、陣地起伏較小時具有良好的估計效果，但當快拍數、信噪比較低或信號模型失配情況下，低空測角性能急劇下降。目前，針對起伏較小的陣地環境下的低空測角問題，文獻[5]提出了一種基于地形修正的合成導向矢量最大似然算法(Synthesized Vector ML, SVML)。該算法考慮地形參數信息，建立精確的信號模型，能極大提高最大似然算法的低空測角性能，算法性能較優。

經典的單脈沖測角作為一種實時性高的測角技術，已廣泛應用于精確跟蹤雷達等，主要適用于單點源的場合。為解決多徑環境下的測角問題，Xu[14]等人在經典單脈沖測角技術的基礎上，根據直達信號仰角和多徑信號仰角關于陣列法線方向的近似對稱性，提出了一種對稱差波束比幅測角方法。通過特定指向的對稱差波束同時接收直達信號和多徑信號，將對稱相干源的仰角估計問題轉化成單點源估計問題，提高了單脈沖測角技術在低仰角條件下的陣地適應性。然而在實際場景下，多徑信號和直達信號通常不完全關于陣列法線對稱，因此需要進行修正對稱差波束。本文從經典多徑信號模型出發，在分析單脈沖測角算法原理以及數據的物理特征基礎上，提出一種改進的對稱和/差波束的低仰角目標DOA估計方法，通過修正的和/差波束中心仰角，提高單脈沖測角技術在低仰角條件下的測角性能及陣地適應性。

1 對稱差波束原理

對于經典單脈沖雷達系統，和波束方向圖是偶函數，差波束是奇函數，故鑒角曲線是奇函數。在多徑信號條件下，誤差單脈沖比為一個復數，信號矢量關系圖如圖1(a)所示，其中Δd和Δi分別為直達波、多徑反射波的差波束信號，Σd和Σi分別為直達波、多徑的和波束信號。通過對差波束的設計，使得多徑差信號Δi仍然與和信號Σi保持同相，則合成的“差通道”信號Δ(=Δd+Δi)與“和通道”信號Σ(=Σd+Σi)仍然保持同向關系，單脈沖比仍然為實數，并且不受反射系數的影響，其矢量圖如圖1(b)所示。

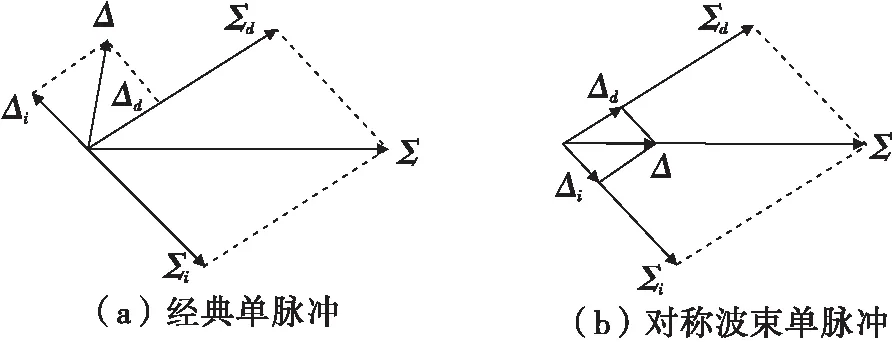
圖1 單脈沖系統和信號、差信號矢量關系圖

文獻[14]考慮的對稱鏡面反射情況。對于經典單脈沖系統，當存在鏡像對稱多徑情況下，即θi≈-θd，單脈沖比為

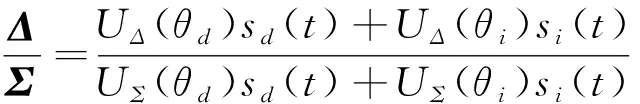
(1)

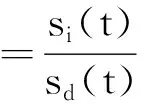
由于直達信號仰角和多徑信號仰角關于陣列法線呈近似對稱，文獻[15]采用對稱差波束進行接收，即差波束關于波束中心仰角成偶對稱，有UΔ(θ)=UΔ(-θ)，則式(1)的誤差信號可表示為

(2)

可以看出，采用對稱差波束有效解決多徑信號對單脈沖測角算法的影響。而且對稱和/差波束的誤差信號只與目標仰角有關，而與多徑信號的反射系數無關，通過計算誤差信號可以準確估計目標仰角。文獻[15]給出了波束對稱中心在0°的對稱差波束的最優權矢量設計。但是在實際陣地，多徑反射波和直達波不是完全關于陣列法線的一對鏡面對稱信號，或者雷達陣列天線通常也是有一定的傾斜，多徑反射波和直達波的對稱中心也不為0°。

2 基于改進和/差波束的低仰角目標DOA估計方法

2.1 信號模型

經典多徑信號模型如圖2所示，假設陣列是由M陣元組成的均勻線陣，陣元間隔為d，正常取半波長，快拍數為L。那么陣列接收信號矢量y(t)可表示為

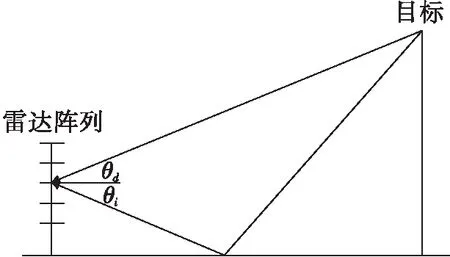
圖2 低仰角測高經典信號模型

其中，θd、θi分別為直達波和多徑反射波波達角，a(θd)表示直達波導向矢量，a(θi)表示多徑信號導向矢量，λ為波長，ρ為反射面復反射系數，s(t)為信號復包絡，n(t)表示均值為0、方差為σ2的復高斯白噪聲。

2.2 改進的對稱差波束權矢量設計

直達信號和多徑信號不是鏡面對稱信號時，是關于某一仰角θt對稱的，且差波束在對稱中心θt的增益最小。為方便推導，假設陣列同時接收方向為θt+θk的直達信號和θt-θk的多徑信號，偏角θk通常不超過波束寬度的二分之一。本文改進的對稱差波束的權矢量wΔ,θt需要滿足以下兩個條件：

1)條件1：對稱差波束要求權矢量wΔ,θt在對稱中心仰角θt處的增益最小，即

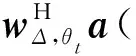
(6)

2)條件2：對稱差波束關于仰角θt呈偶對稱，指向分別為θt±θk，且權矢量wΔ,θt在波束指向θt±θk處具有相同的增益，即

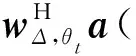
(7)

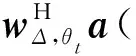
(8)

其中，gk表示差波束在波束指向θt±θk方向上的增益。

令R=[a(θt-θk)a(θt)a(θt+θk)]，d=[gk0gk]T，式(6)、式(7)、式(8)寫成矩陣形式為

RHwΔ,θt=d

(9)

根據最小二乘法，差波束的權矢量為

wΔ,θt=R(RHR)-1d

(10)

其中，(RHR)-1可進一步表示為

(11)

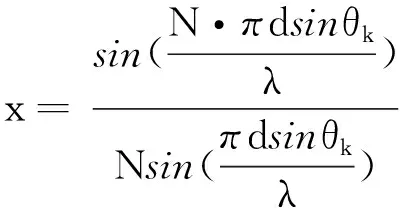
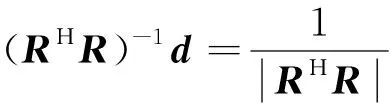
(12)

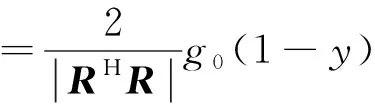
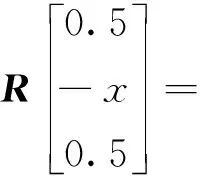
(13)

因此，歸一化的差波束權矢量wΔ,θt為

wΔ,θt=Re[a(θt+θk)]-xa(θt)

(14)

其中，Re[·]表示取實部。采用計算機仿真實驗分析所提對稱和差波束的方向圖及鑒角曲線，仿真參數為24陣元的等距線陣，波長1m，陣元間距為半波長，中心仰角θt=0°。圖3和圖4分別給出了對稱和/差波束方向圖及其鑒角曲線。

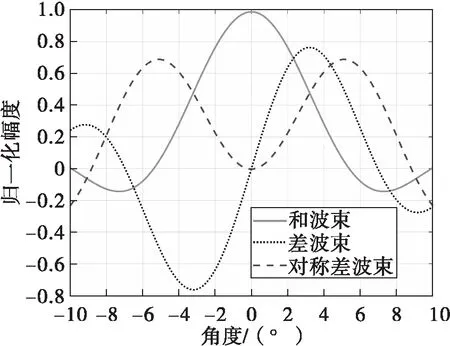
圖3 波束方向圖

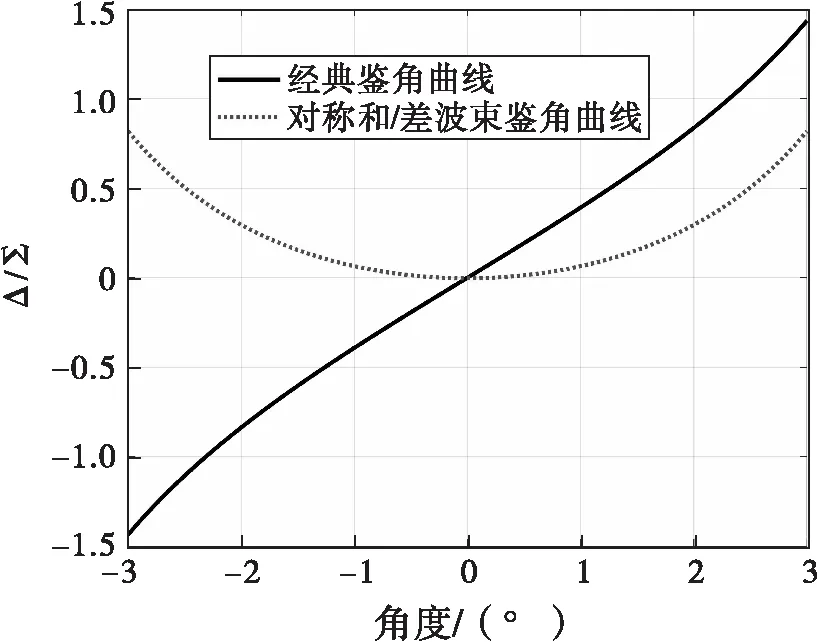
圖4 經典單脈沖與對稱波束單脈沖鑒角曲線

可以看出，所提方法的和/差波束均是關于波束中心仰角成偶對稱，同時接收直達信號和多徑信號，通常誤差曲線僅考慮目標仰角大于0的部分。此時，對稱和/差波束的鑒角曲線近似是一條拋物線，可采用二次函數近似擬合為

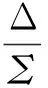
(15)

對式(15)求微分，根據對稱和/差波束鑒角曲線得到測角誤差為

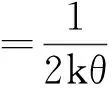
(16)

可以看出，測角精度與目標仰角和擬合系數k有關，擬合系數k越大，算法估計精度越高。因此要設計最優的對稱差波束，使得擬合系數k最大。由文獻[15]可知，當θk趨近于0時，對稱差波束擬合系數k值最大，此時對稱差波束稱為“最優”對稱差波束。

在理想多徑條件下，陣列接收到的直達波與多徑反射信號關于中心仰角θt=0°呈對稱關系。圖5對比中心仰角θt=0°，θk分別取不同的值時，對稱和/差波束誤差曲線。可以看出，當θk逐漸逼近0°時，誤差曲線在中心仰角處的曲率最大，此時測角精度最高。若考慮直達信號和多徑反射信號不完全關于θt=0°對稱，此時需要進行動態修正。圖6給出了對稱和/差波束誤差曲線由波束中心仰角修正θt=0°到θt=-0.7°的過程。可以看出，修正過程實際上就是對誤差曲線進行平移處理。

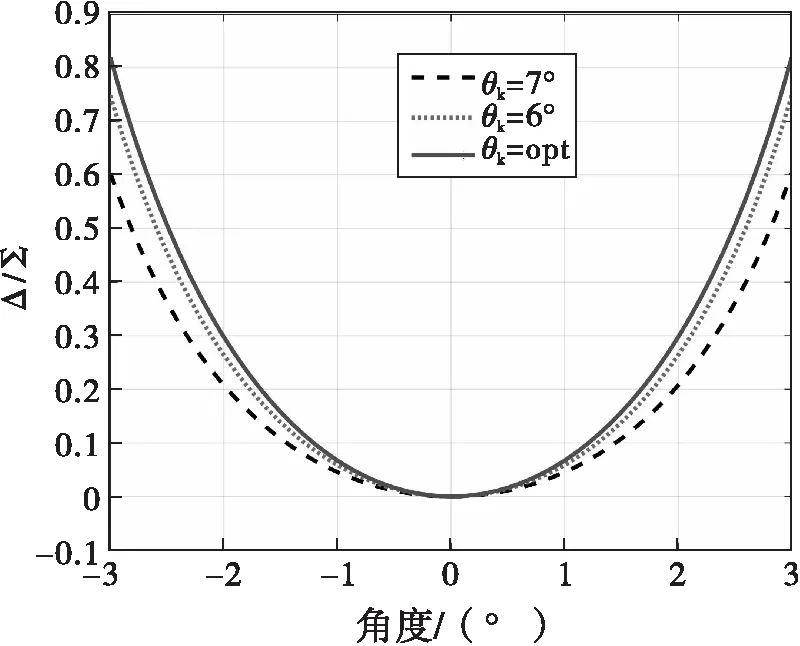
圖5 不同θk對應的對稱和/差波束鑒角曲線

圖6 誤差曲線修正過程

綜上，改進的對稱和/差波束低仰角目標DOA估計方法的具體步驟可以總結為：

1)按常規數字波束形成(DBF)技術估計目標的仰角，若目標仰角大于一個波束寬度，則應用數字單脈沖測角技術進行仰角測量，否則按一下步驟進行；

2)當DBF的峰值對應的仰角小于一個波束寬度(θ3dB)時，在(0，θ3dB)范圍內設置不同的仰角θd，根據雷達架高、地面起伏高度等參數信息，計算反射波的仰角θi≈-arcsin(sin(θd)+2hr/Rd)，再計算直達信號和多徑信號的對稱中心仰角θt=(θi+θd)/2。其中，Rd為直達波的波程(即目標距離)，hr為雷達陣列天線中心的架高；

3)根據式(14)設計對稱差波束，計算關于中心仰角θt對稱的差波束的權wΔ,θt；

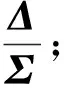
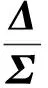
3 仿真數據分析

仿真1：對比動態修正中心仰角算法和固定中心仰角算法測角性能 。

仿真條件：米波雷達陣列結構為24陣元均勻線陣，波長1m，快拍數為1，陣元間距為半波長，波束寬度θ3dB=4.2°，目標仰角范圍是0.4°～2°，地面衰減系數為0.8exp(j8π/9)，信噪比30dB。圖7給出了SSMUSIC、SVML、文獻[14]所提算法和本文算法的測角均方根誤差與目標仰角的關系圖。從圖7可以看出，對于SSMUSIC算法，隨著目標仰角的增大，測角均方根誤差由0.3°下降至0.11°；對于SVML算法，測角均方根誤差由0.27°下降至0.14°；對于文獻[14]中的算法，測角均方根誤差由0.26°下降至0.11°；對于本文所提算法而言，測角均方根誤差由0.22°下降至0.09°，算法性能優于已有的多種超分辨算法，且改進的對稱差波束方法性能優于文獻[14]提出的算法。

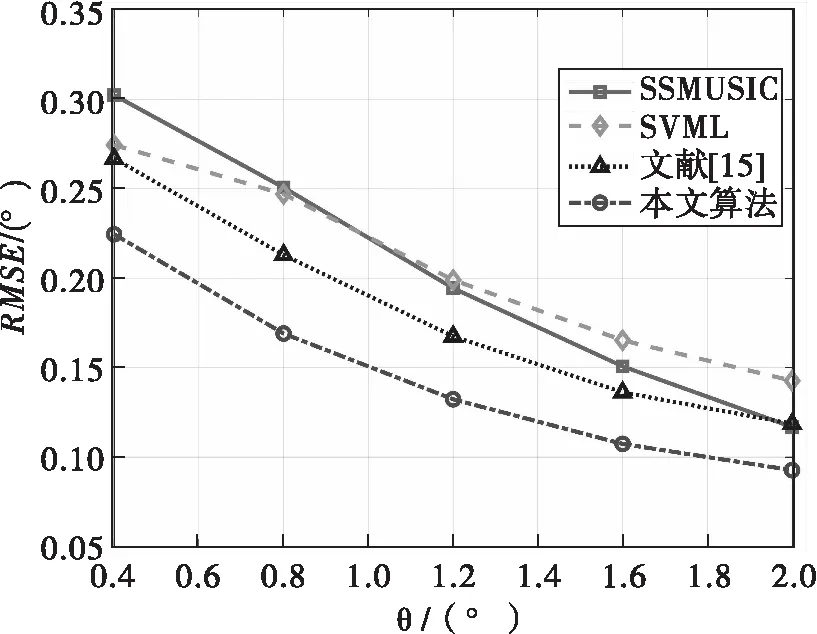
圖7 不同仰角測角的均方根誤差

仿真2：對比不同信噪比情況下所提方法的有效性。

仿真條件：米波雷達陣列結構為24陣元的均勻線陣，波長1m，陣元間距為半波長，快拍數為1，陣列波束寬度θ3dB=4.2°，單天線信噪比范圍是0dB～30dB，目標仰角為0.4°，地面衰減系數為0.8exp(j8π/9)。圖8給出了SSMUSIC算法、SVML算法和本文所提算法的測角均方根誤差與信噪比的關系曲線。

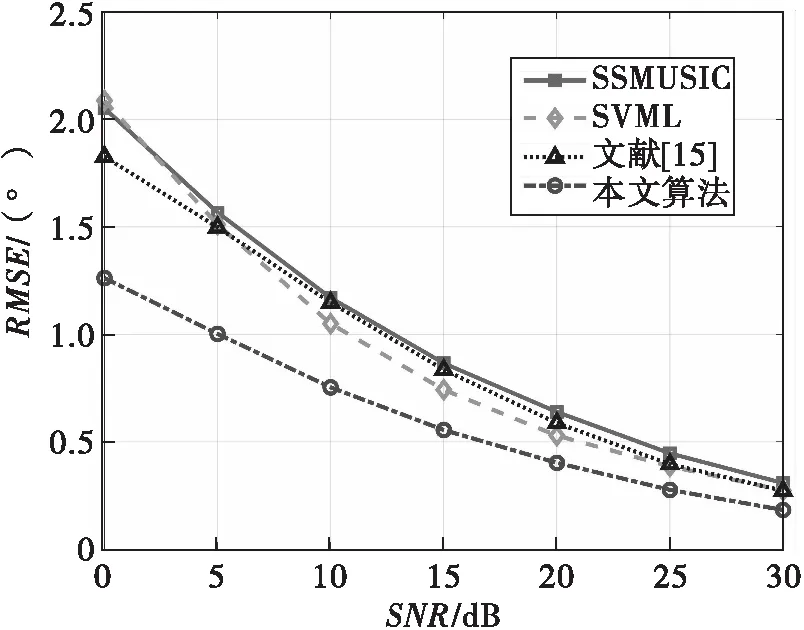
圖8 測角均方根誤差與信噪比關系曲線

可以看出，SSMUSIC、SVML及文獻[14]的算法性能近似，隨著信噪比的增大，測角精度由2.08°逐漸下降至0.27°；對于本文所提算法，其測角均方根誤差由1.26°下降至0.18°，在所有信噪比條件下均優于SSMUSIC、SVML和文獻[14]提出的算法。因此，所提算法更能適應于平坦陣地環境下的低仰角測高問題，算法性能較優。

4 實測數據分析

對某型米波雷達的兩條航線實測數據進行統計分析，陣元結構為24陣元的等距線陣，分別采用DBF算法、APML算法、SSMUSIC算法和本文所提出的對稱和/差波束算法對目標點跡數據進行DOA估計。圖9和圖10分別給出了兩條航線的實測數據處理結果。其中，圖9(a)和圖10(a)分別為兩條航線的航跡圖；圖9(b)和圖10(b)分別給出多種算法的測角結果；圖9(c)和圖10(c)分別給出多種算法的測角誤差結果。可以看出，本文所提在低仰角條件下的測角性能優于其他算法，所提算法的測角結果更加平滑、穩定，起伏較小。表1分別統計兩條航線的點跡數及各算法的測角均方根誤差。對于航線一：DBF算法的測角均方根誤差約為0.26°；APML算法的測角均方根誤差約為0.44°；SSMUSIC算法的測角均方根誤差0.20°；而本文所提算法的測角均方根誤差約為0.04°。對于航線二：DBF算法的測角均方根誤差約為0.31°；APML算法的測角均方根誤差約為0.19°；SSMUSIC算法的測角均方根誤差約為0.30°；而本文所提算法的測角均方根誤差約為0.04°。實驗數據表明，本文提出算法優于SSMUSIC算法和APML算法，測角性能良好，可靠性高，適合部分陣地環境下的低仰角測量問題。

圖9 航線一實測數據結果

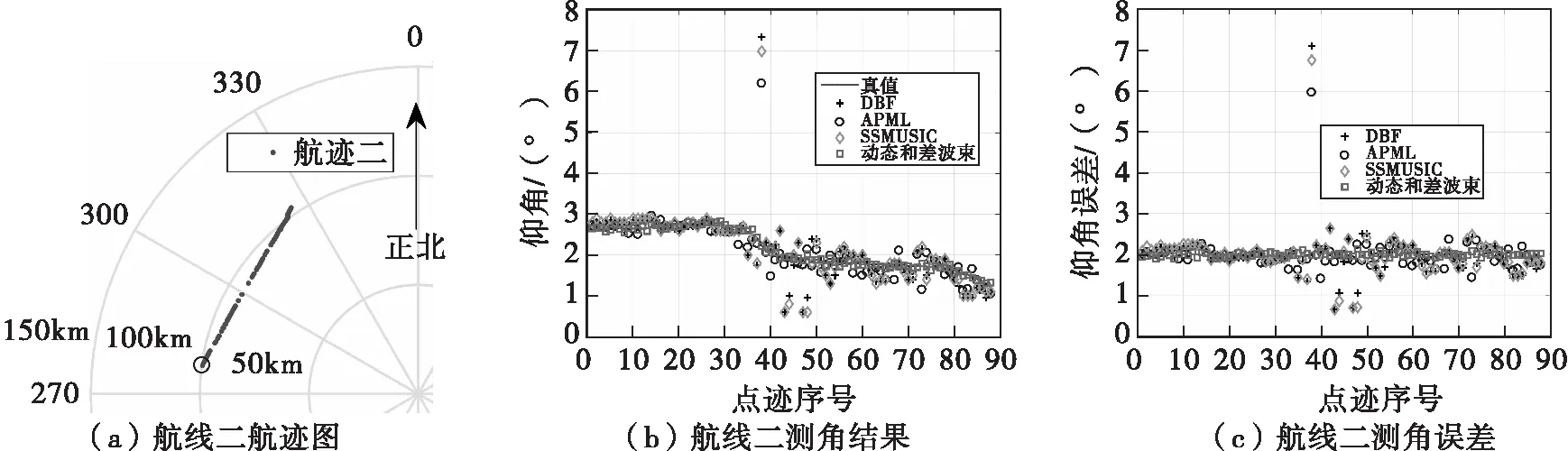
圖10 航線二實測數據結果

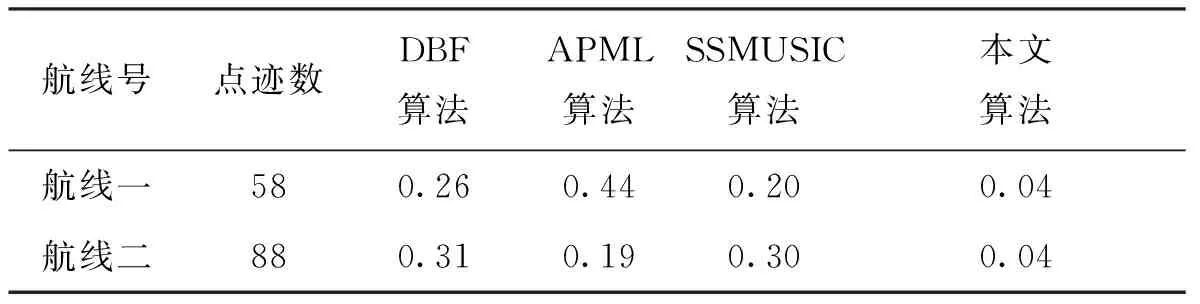
表1 實測數據對仰角測量的均方根誤差/(°)

5 結束語

本文針對米波雷達低仰角目標DOA估計問題，首先回顧了經典信號模型下的單脈沖測角方法，根據直達波信號與多徑反射波信號的近似對稱性，設計了最優的對稱和/差波束，并在此基礎上提出一種改進的對稱和/差波束測角方法，通過調整波束中心指向及差波束指向，提高單脈沖測角方法在低仰角條件下的估計精度及其陣地適應性。通過計算機仿真及實測數據驗證，所提方法在低仰角條件下算法性能優于已有的多種超分辨算法，可靠性高。