非等間隔采樣條件下卡爾曼濾波器設計與實現
楊 森 羅利強 高 劍 張西平
(西安電子工程研究所 西安 710100)
0 引言
卡爾曼濾波算法廣泛應用于導航、通信等領域,該算法通過遞推方式獲得新的狀態估計,實時獲取估計信息,而不需要存儲大量的歷史信息。在雷達數據處理過程中,需利用當前時刻的量測信息來預測下一時間的估計信息,因此卡爾曼濾波算法在雷達數據處理中得到了廣泛的應用。
在工程實際運用中,雷達采樣間隔并不都是等周期的,此時若仍采用恒定的采樣間隔進行計算,可能造成系統的初始狀態和初始協方差的假設值偏差過大,導致濾波發散。為了克服非等間隔采樣條件下跟蹤精度不佳的問題,本文提出了一種非等間隔采樣條件下卡爾曼濾波器設計與實現方法,該方法通過算式推導,從原理上獲得了協方差的精確解,完成濾波迭代,不僅避免了由于協方差近似解造成的濾波發散的風險,而且可同時應用于非等間隔、等間隔采樣條件下卡爾曼濾波器的設計與實現,且計算量沒有明顯變化,拓寬了已有濾波算法應用場合。
1 非等間隔采樣條件下卡爾曼濾波器的設計
以三坐標雷達的數據處理問題為例,非等間隔采樣條件下卡爾曼濾波器的設計包含以下兩部分內容:一是非等間隔采樣條件下濾波器參數的初始化;二是非等間隔采樣條件下的濾波器迭代過程。其中,濾波器參數的初始化主要包括初始狀態估計和初始協方差估計兩個部分;濾波器迭代過程中,主要包括狀態、協方差預測,量測預測,新息、增益等的計算,最終完成狀態更新以及協方差更新。
1.1 非等間隔采樣條件下濾波器參數初始化
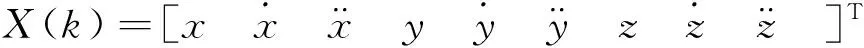
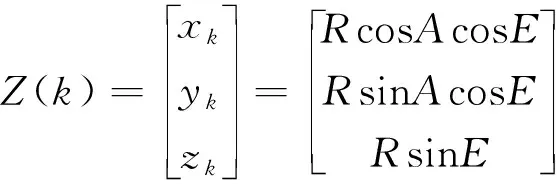
(1)
其中,、、分別為極坐標系下距離、方位、俯仰的量測值。
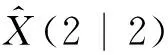
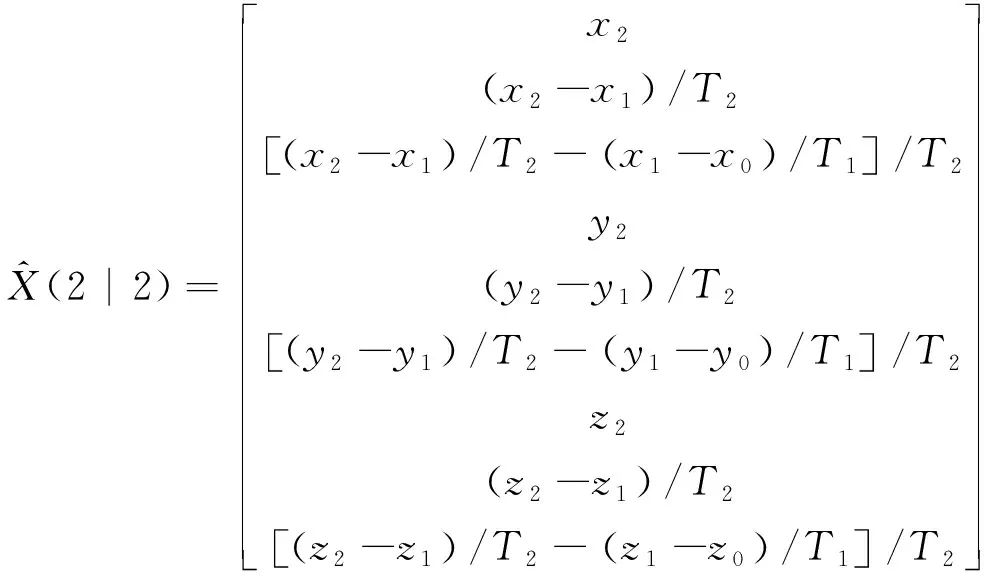
(2)
式(2)中,為量測(0)與(1)的時間間隔,為量測(1)與(2)的時間間隔。
在直角坐標系下,時刻的量測噪聲協方差()可表示為
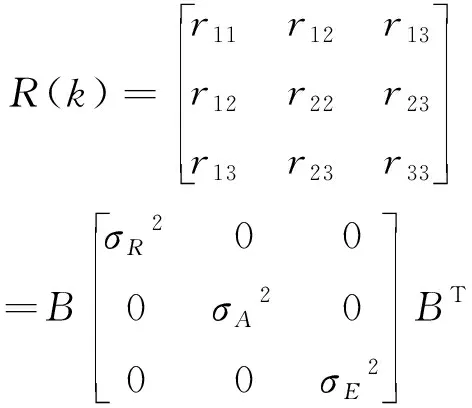
(3)
式(3)中,為徑向距離測量誤差的方差,和分別為方位角和俯仰角測量誤差的方差,而
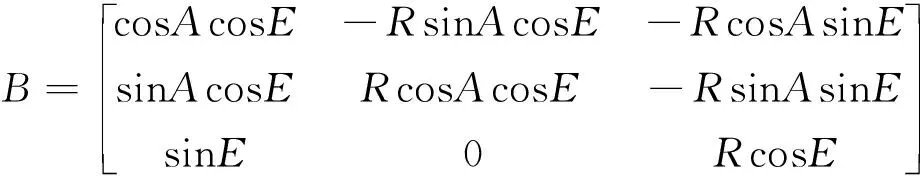
(4)
初始協方差(2|2)為
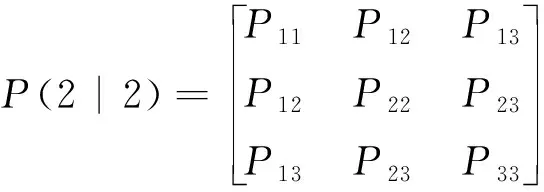
(5)
式(5)中,、、、、、為分塊矩陣,且
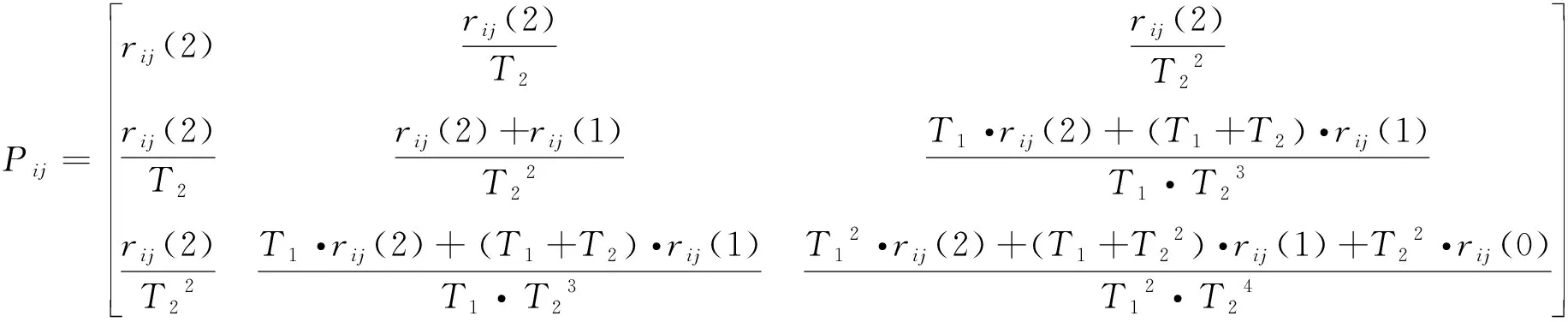
(=1,2,3;=1,2,3)
(6)
1.2 濾波器迭代
在完成濾波器初始化的基礎上,利用后續更新量測,依次完成狀態、協方差預測,量測預測,新息、增益等的計算,完成濾波器狀態更新迭代。
在非等間隔采樣條件下,濾波器迭代過程與等間隔采樣條件下基本一致,其中,狀態轉移矩陣()、量測噪聲的協方差(+1)以及過程噪聲的協方差()的取值與時間間隔有關,因此在迭代過程中,需實時更新以上結果并代入。
離散時間系統的狀態方程可表示為式(7)。
(+1)=()()+()()+()
(7)
量測方程可表示為
(+1)=(+1)(+1)+(+1)
(8)
狀態的一步預測為
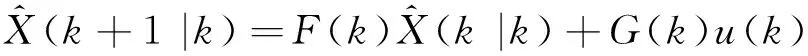
(9)
量測的預測為
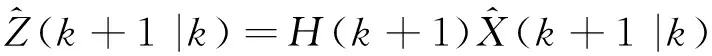
(10)
新息表示為式(11)。
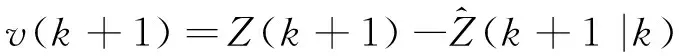
(11)
協方差的一步預測為
(+1|)=()(|)′()+()
(12)
量測的新息協方差表示為
(+1)=(+1)(+1|)·
′(+1)+(+1)
(13)
增益為
(+1)=(+1|)·
′(+1)(+1)
(14)
可得狀態更新方程和協方差更新方程為
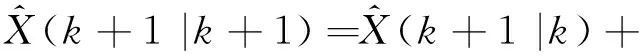
(15)
(+1|+1)=(+1|)-
(+1)(+1)′(+1)
(16)
卡爾曼濾波流程圖如圖1所示。
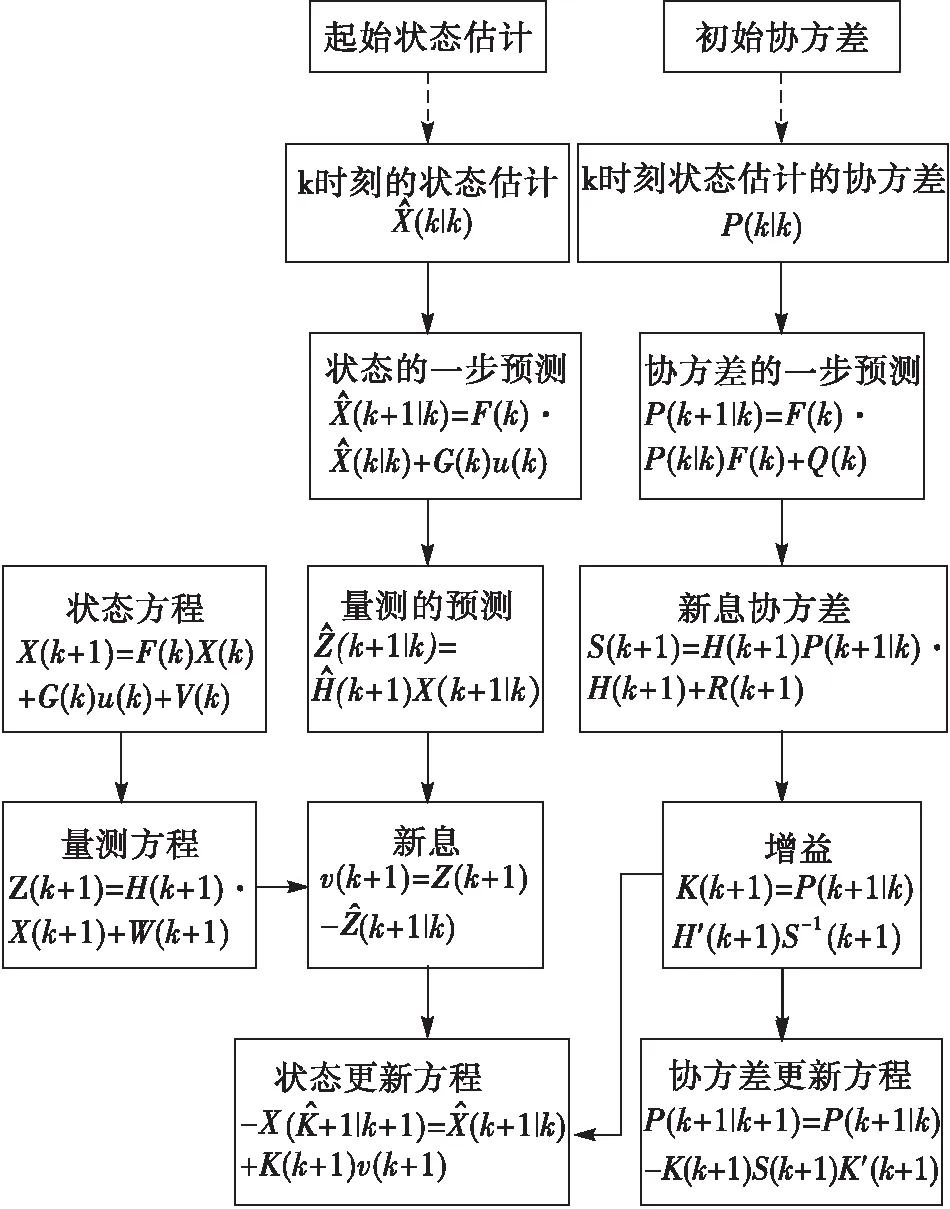
圖1 卡爾曼濾波流程圖
2 性能驗證
2.1 仿真分析
1)場景設置
模擬運動目標在空間做等高勻加速運動,初始速度為200m/s、加速度為1m/s,飛行高度1500m;雷達測距精度70m,測角精度(方位角、俯仰角)均為03°,采樣點數取100;雷達工作在扇掃工作模式(扇掃周期為2s),此時相鄰兩次掃描到同一目標的時間間隔不同,其中第一、二個掃描時刻的時間間隔約為15s,第二、三個掃描時刻的時間間隔約為05s。
2)非等間隔采樣條件
采用文中提出的方法,在濾波迭代過程中,實時更新采樣間隔,即實時代入=15s、=05s。其中一次仿真結果的示意圖如圖2所示。

圖2 真實軌跡、觀測軌跡與濾波估計
500次蒙特卡洛仿真條件下,距離、方位角和俯仰角誤差的精度曲線如圖3至圖5所示。
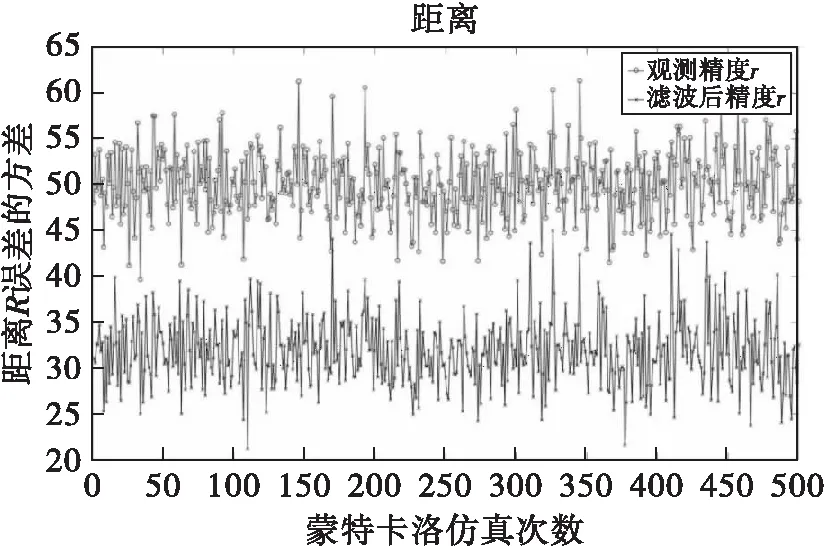
圖3 距離誤差的精度曲線
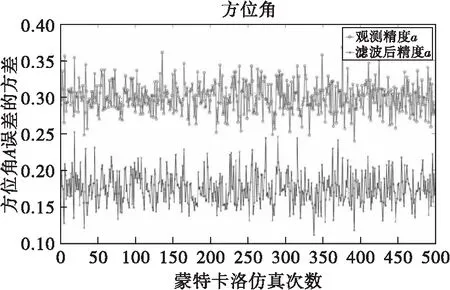
圖4 方位角誤差的精度曲線
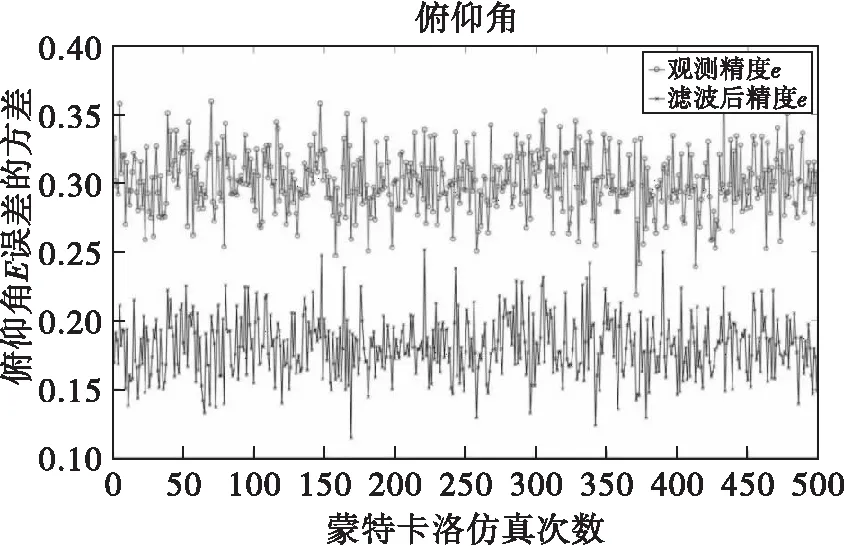
圖5 俯仰角誤差的精度曲線
在仿真過程中,測距精度為50m,測角精度均為0.3°。對500次蒙特卡洛仿真結果求均值,距離精度為31.9045m,方位角精度為0.1747°,俯仰角精度為0.1812°。
3)等間隔采樣條件
采用等間隔采樣卡爾曼濾波器作為對比,在濾波迭代過程中,用扇掃周期的一半近似表示采樣間隔,即T=T=1s。
500次蒙特卡洛仿真條件下,距離、方位角和俯仰角誤差的精度曲線如圖6至圖8所示。
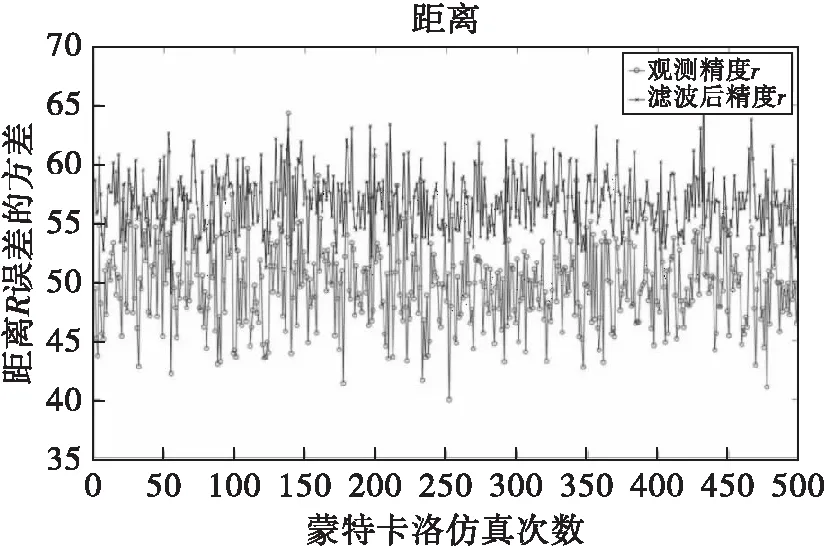
圖6 距離誤差的精度曲線
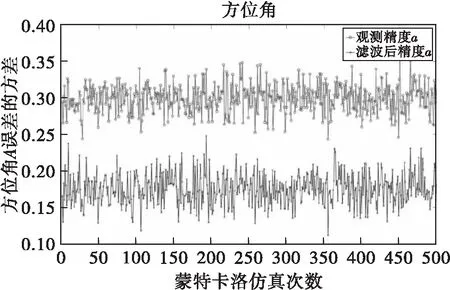
圖7 方位角誤差的精度曲線
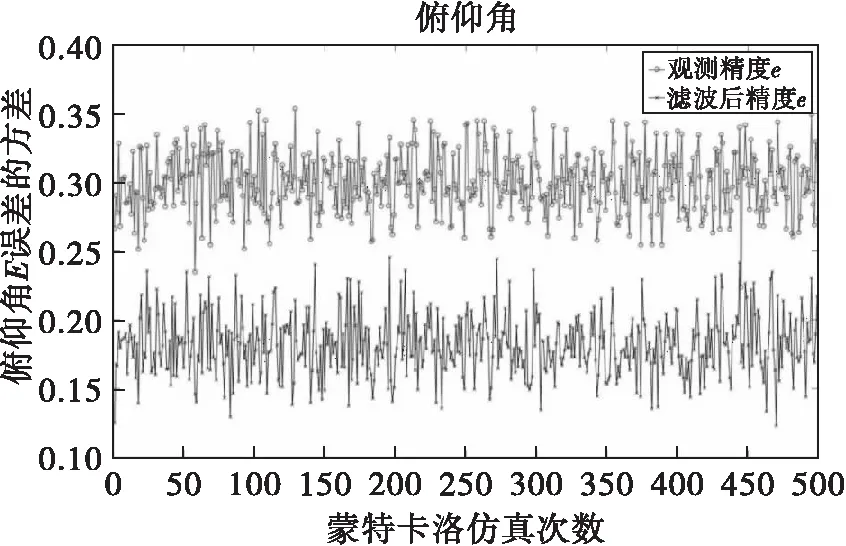
圖8 俯仰角誤差的精度曲線
對500次蒙特卡洛仿真結果求均值,距離精度為56.8797m,方位角精度為0.1750°,俯仰角精度為0.1817°。
2.2 實測結果
兩種模式下誤差的精度對比結果如表1所示。
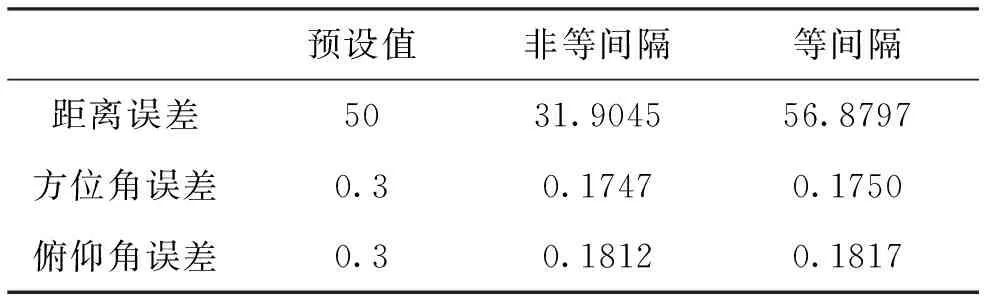
表1 兩種濾波方式結果對比
非等間隔采樣條件下(=1.5s,=0.5s)進行迭代濾波,距離、方位角和俯仰角誤差的精度與預設值相比均變小,符合工程實際運用要求。觀察采樣間隔==1s時濾波結果,可以看出,雖然方位角、俯仰角的濾波效果與前者基本持平,但是距離的濾波效果不佳,甚至出現濾波精度不如觀測精度的現象。
3 結束語
本文提出了一種非等間隔采樣條件下卡爾曼濾波器設計與實現方法,該方法在非等間隔采樣條件下完成濾波器參數初始化以及濾波器迭代,在計算量沒有明顯增加的情況下,濾波結果精度更高,算法有效性和可靠性高,且易于實現,具有一定的工程應用價值。

