相似三角形中的求值問題

王東東

(山東省新泰市泉溝鎮初級中學 271200)

相似三角形是在初中平面幾何中一個非常重要的內容，包括相似三角形的定義、判定、性質等，同時涉及特殊的直角三角形相似的判定及直角三角形的射影定理，是平面幾何的重要知識點與考點之一．在破解一些相關的平面幾何求解問題中，巧妙借助相似三角形的相關知識來處理，經常可以合理轉化，化難為易，出奇制勝．以下結合幾類常見的相似三角形中的求值問題，如計數、長度、比值、面積以及綜合應用等相關的求值題加以剖析．

1 計數問題

例1如圖1所示，在△ABC中，ED∥AB，FG∥AC，PH∥BC，相應的交點分別為A1、B1、C1，則圖中與△ABC相似的三角形的個數為____個．

分析根據相似三角形的性質，要判斷圖中與△ABC相似的三角形，可以從平行這個條件出發，找到對應相等的角，從而得以確定兩三角形相似．

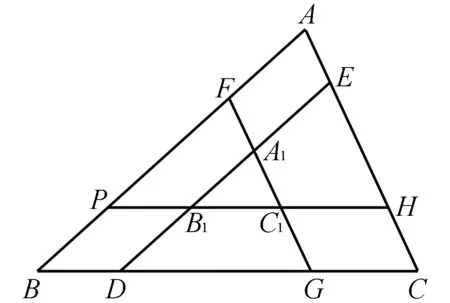
圖1

解析由于PH∥BC，那么∠APH=∠B，而∠A是公共角，則△APH∽△ABC，同理可以判斷△BGF∽△ABC，△CED∽△ABC，進一步，FG∥AC，那么∠PFC1=∠A，又∠FPC1=∠B，△FPC1∽△ABC，同理可以判斷△DGA1∽△ABC，△HEB1∽△ABC，而ED∥AB，那么∠FPC1=∠A1B1C1，而∠FPC1=∠B，則∠A1B1C1=∠B，同理可得∠A1C1B1=∠C，則△A1B1C1∽△ABC，所以圖中與△ABC相似的三角形的個數共有7個，故填答案：7．

點評三角形相似的判定關鍵是結合三角形相似的性質加以分析，在求解三角形相似的問題的過程中，往往是在熟練掌握相應性質的基礎上，結合直觀圖形加以正確分析．

2 長度問題

例2如圖2，正方形ABCD的邊長是2，BE=CE，MN=1，線段MN的兩端在CD、AD上滑動，當DM=____時，△ABE與△DMN相似．

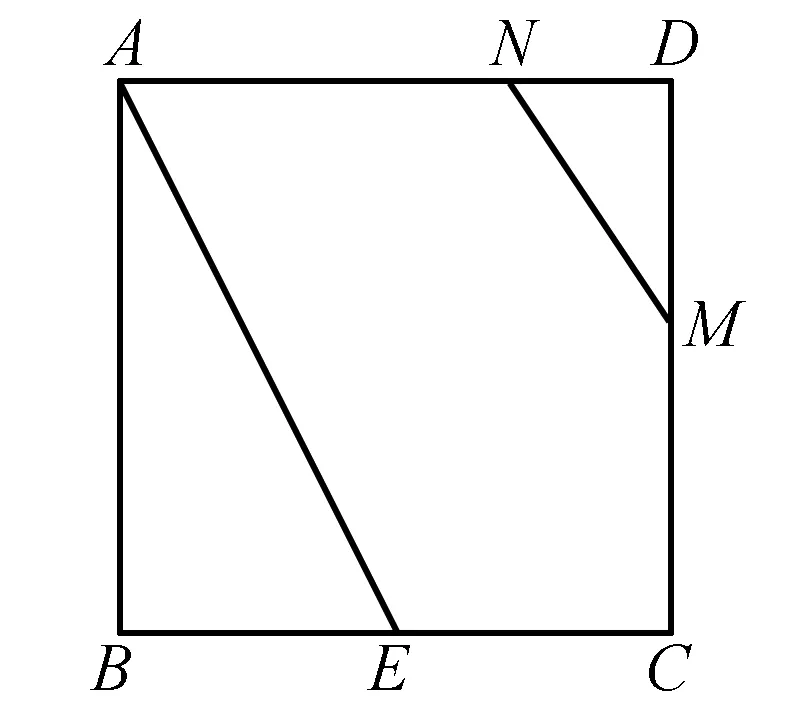
圖2

分析因為兩個三角形都是直角三角形，當且僅當兩直角邊之比相等時它們相似，據此可列一個方程，再結合MN=1列方程組，解此方程組得DM的值．

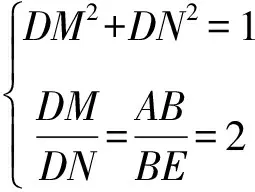
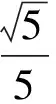
點評本題是探求兩個三角形相似的條件問題，實質是以三角形相似為條件，求線段長度問題，關鍵是找到相應的比值并結合相關條件加以求解．特別在實際求解時，要全面考慮，比如本例中就容易忽視其中的一種情形．

3 比值問題

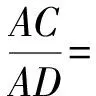
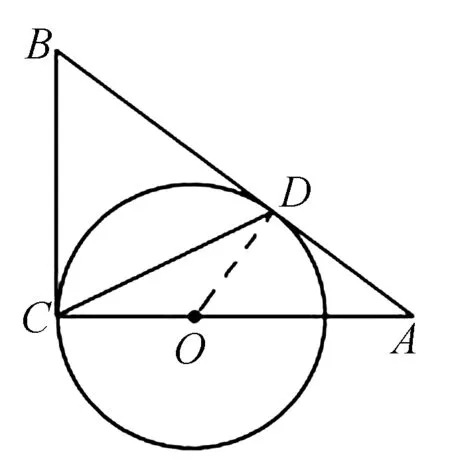
圖3

分析通過作出輔助線OD，根據兩直角三角形△ADO與△ACB相似來建立關系式，結合題目條件來證明對應的等式成立．

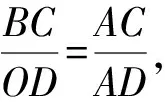
故填答案：2．

點評結合輔助線的構造，利用直角三角形的相似以及相關條件加以確定相關的求值問題．對于平面幾何中的求值問題，關鍵是正確引入相關的輔助線，加結合相應條件的變換與轉移，從而達到求值的目的．

4 面積問題

例4如圖4所示，在四邊形ABCD中，E是AB上一點，EC∥AD，DE∥BC，若S△BEC=1，S△ADE=3，則S△CDE的值為____．

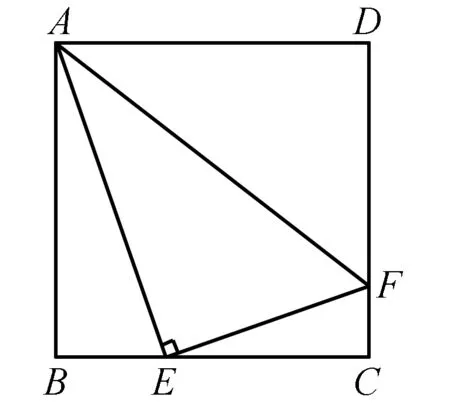
圖4

分析根據平行線的性質轉化三角形的面積比為對應的線段比，結合平行線所確定的角的關系證明△BEC∽△EAD，再由比例性質轉化為面積之間的比值即可求解S△CDE的值．

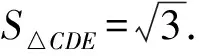
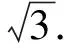
點評通過平行線的性質，結合相似三角形中的對應邊的比例關系與相應的三角形的面積的比例關系的轉化與應用來分析與處理問題．

5 綜合應用問題

例5如圖5，已知正方形ABCD的邊長為4，E是BC上的點，EF⊥AE交CD于F．試猜想：點E在什么位置時，△ADF的面積最小？最小面積是多少？并證明你的結論．

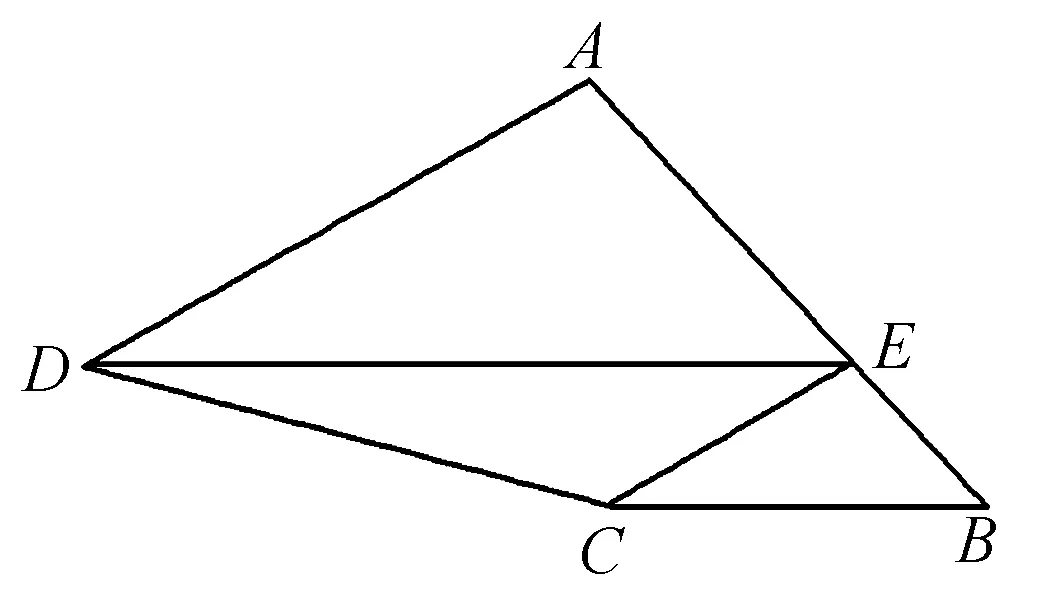
圖5

分析要猜想對應點的位置，關鍵是結合相應的幾何圖形與關系式加以分析判斷，巧妙引入未知數，通過建立有關面積的函數關系式，利用函數的最值問題來判斷對應的幾何問題．

解析當點E是BC的中點時，△ADF的面積最小，最小面積是6．

下面證明以上猜想的結論：

設BE=x，那么EC=4-x，

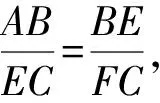
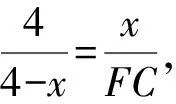
可得

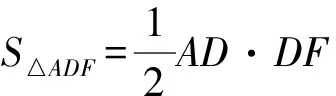
故當x=2時，即E是BC的中點時，△ADF的面積最小，最小面積是6．

點評在平面幾何問題中，往往可以有機地結合相應的函數等相關問題，利用函數等相關問題的性質來處理與解決對應的平面幾何問題，這是一種非常巧妙與有效的辦法．關鍵是將平面幾何問題進行代數化，并加以正確的分析與判斷．

相似三角形及其應用是在初中平面幾何的基礎知識上的進一步拓展與提升，特別是在一些平面幾何的求值問題中，合理借助輔助線與相似三角形的構造，通過對判定、性質等一系列的轉化與應用，有效培養學生邏輯推理能力、圖形直觀能力與創造思維能力，其也是歷年中考數學命題中的一大熱點問題，應該引起一線教師高度重視．