含缺陷石墨烯彈性性能的分子動力學模擬

鄧雅丹，周昆，黃君，黃立新,2*

(1.廣西大學土木建筑工程學院，南寧 530004; 2.廣西大學工程防災與結構安全教育部重點實驗室，南寧 530004)

石墨烯是由碳原子組成的蜂窩形納米材料，它的比表面積大、穩定、柔韌并且具有良好的導電性、導熱性、光學特性和機械性能，在電子[1-3]、航空航天[1]、新能源電池[2, 4]、生物醫學[5-6]等領域都具有良好的應用前景，石墨烯性能的研究具有十分重要的意義。為了更好地研究石墨烯的性能，石墨烯的制備方法也在不斷發展，范金辰[7]采用超聲剝離法得到功能化的石墨烯片層；Kumar等[8]采用原位微波法制備三維(3D)還原氧化石墨烯納米片；陳吉[9]采用化學氣相沉積法制備石墨烯。以上研究為高性能石墨烯的制備提供了簡便、有效的方法。石墨烯在各個領域的研究，都是基于理想即無缺陷的石墨烯，然而在石墨烯的制備過程中，或多或少都會產生一定的缺陷，這些缺陷會對石墨烯的性能產生一定的影響，因此研究含缺陷石墨烯的性能是一項十分重要的工作。

石墨烯的缺陷主要有3種：空位缺陷、表面吸附雜質缺陷和拓撲缺陷[10]。空位缺陷包括單空位缺陷、雙空位缺陷和多空位缺陷。所謂的空位缺陷，就是因結構缺失原子，所造成原有位置的空缺，因缺失原子數目的不同，其名稱也不同，缺失一個原子即單空位缺陷，缺失兩個相鄰原子即雙空位缺陷，缺失3個及3個以上相鄰原子即多空位缺陷。表面吸附雜質缺陷即當石墨烯的原子離開晶格，與其相鄰的3個C原子各多出一個懸空鍵，以此來吸引外來原子。拓撲缺陷常見的是Stone-Wales缺陷(以下簡稱SW缺陷)，SW缺陷不含原子的缺失，它只是其中一個C-C鍵通過鍵角旋轉90°，缺陷部分的形狀由4個六邊形變成2個五邊形和2個七邊形。

He等[11]基于分子動力學模擬研究了Stone-Thrower-Wales(STW)缺陷的取向和傾斜角對石墨烯力學性能的影響，可知STW-1缺陷和STW-2缺陷的石墨烯，其扶手型方向的強度與鋸齒型方向的強度具有差異，且機械性能取決于缺陷的傾斜角。Mortazavi等[12]采用分子動力學模擬，研究了點空位、雙空位和Stone-Wales缺陷對單層石墨烯片熱導率和拉伸響應的影響，可以得到石墨烯的彈性模量、拉伸強度和斷裂應變隨著缺陷濃度的增加而降低，且熱傳導更容易受到缺陷影響的結論。Lei等[13]通過分子動力學模擬，研究了各種點缺陷和裂紋對4種石墨烯同素異形體力學性能的影響，研究發現它們的楊氏模量相較于拉伸強度而言，對各種類型的點缺陷更不敏感，而對裂紋而言，其楊氏模量和拉伸強度都顯著下降。Ajori等[14]利用分子動力學模擬，研究了映射缺陷和隨機缺陷對石墨烯同素異形體γ-graphyne的楊氏模量、極限應力和應變以及泊松比的影響，結果表明，γ-graphyne的強度和剛度低于石墨烯，此外，隨機缺陷的力學性質變化比映射空位缺陷大。

由于石墨烯的缺陷是不可避免的，缺陷對石墨烯彈性性能的影響比較復雜，缺陷的位置、形狀以及原子缺失率如何影響石墨烯的彈性性能，仍然存在需要解決的問題，有必要開展進一步的研究工作。因此，現采用分子動力學模擬的方法，研究空位缺陷的位置、形狀以及原子缺失率對石墨烯彈性性能的影響，探究空位缺陷的位置、映射橫向長條狀缺陷、映射縱向長條狀缺陷、映射圓孔狀缺陷和隨機缺陷等因素導致石墨烯楊氏模量減少的規律。

1 分子動力學方法和理論

基于分子動力學理論，采用軟件Materials Studio(MS)進行力學性能計算。MS是一款用于創建分子結構模型，并對模型進行計算分析以研究其性質的模擬軟件[15]。采用腳本進行模擬計算，MS的腳本采用一種功能強大、應用廣泛且靈活性強的計算機程序Perl語言進行計算。

在模擬的過程中，由于物體的宏觀性質需要足夠多的微粒，而計算機無法滿足其龐大的計算，就要考慮邊界部分所帶來的影響，因此，為了消除邊界效應，該模型采用周期性邊界條件。COMPASS(condensed-phase optimized molecular potentials for atomistic simulation studies)力場[16]用于原子模擬，COMPASS的能量表達式[17]為

Utotal=Ubonded+Unonbonded

(1)

Ubonded=Udiagonal+Ucross-coupling

(2)

Unonbonded=Uij+Uelec

(3)

式中：Utotal為總能量；Ubonded為鍵合項能量；Unonbonded為非鍵合項能量；Udiagonal為對角的交叉偶合項；Ucross-coupling為非對角的交叉偶合項，非鍵合項能量為范德華能Uij與庫倫能Uelec之和。

(4)

(5)

(6)

(7)

本模型是在NPT系綜[19]即恒定的粒子數、恒定的體積及溫度下進行的，同時采用可控制各向異性加壓的Souza-Martins恒壓器進行調節，時間常數為10 ps。為了使溫度保持穩定，采用Nose-Hoover-Langevin(NHL)恒溫器，在恒溫器變量中引入摩擦項和噪音項，使其收斂速度更快。并且在所有情況下都使用1 fs的固定時間步長。

2 石墨烯分子動力學建模及楊氏模量計算方法

2.1 建模步驟

(1)在MS 8.0軟件中導入石墨烯的單晶胞模型，創建含有25×15×1個正六邊形(碳原子數為1 500)的石墨烯超晶胞模型，Lx=6.047 nm，Ly= 6.434 nm，如圖1所示。

圖1 石墨烯分子動力學模型

(2)對模型進行幾何優化，細化結構的幾何形狀，直到結構的總能量被最小化，優化后的結構對應于勢能面中的最小值。

(3)采用腳本對優化后的模型分別沿y方向和x方向施加應力，如圖2(a)所示。設置初始應力值為20 GPa，然后依次遞增，每次增加20 GPa，每個應力值的平衡步數設置為500，每500 步生成一幀，每一幀統計一次應力應變數值。

(4)當應力大小增大至500 GPa時，可得出對石墨烯模型施加y方向的應力-應變數值。

(5)重復同樣的步驟，對模型施加x方向的應力，如圖2(b)所示，即可得出石墨烯模型對應的應力-應變數值。

圖2 石墨烯模型施加應力

2.2 楊氏模量的計算方法

按照2.1節的建模步驟，分別沿y方向和x方向施加應力，即可得出石墨烯模型對應的應力-應變數值，如表1所示。根據表1繪制應力-應變關系圖，如圖3所示。從圖3中可以發現，當應變達到0.3時，應力-應變曲線出現明顯的拐點，因此采取應變為0～0.25的曲線段進行最小二乘法擬合，計算楊氏模量[20-22]。

圖3 石墨烯模型施加應力后的應力-應變關系圖

設應變為ε，應力為σ，E為楊氏模量，則方程為

σ=Eε

(8)

采用最小二乘法進行直線擬合[23]，得到楊氏模量計算公式為

(9)

將表1中應變為0～0.25區間內的應力-應變數值組代入式(9)，即可求出楊氏模量E的值，即Ey=1.179 TPa，Ex=1.161 TPa。

3 結果與分析

3.1 無缺陷石墨烯的楊氏模量

通過MS軟件計算，對表1應力-應變數值組進行最小二乘法的直線擬合，所得石墨烯楊氏模量與文獻結果進行對比，如表2所示。從表2可以看出，石墨烯楊氏模量的文獻值在1.00～1.24 TPa，本文模型的楊氏模量值在合理范圍之內，說明本文方法適用于研究石墨烯的力學性能。

表1 模型施加應力后的應力-應變數值

表2 石墨烯的楊氏模量與文獻結果對比

3.2 空位缺陷位置對石墨烯力學性能的影響

由于缺陷是不可避免的，缺陷會對石墨烯的力學性能產生一定的影響，為了研究缺陷產生的位置是否也會對石墨烯的性能產生影響，設計了兩組單空位缺陷，第一組為縱向方位缺陷，包括上邊緣缺陷、偏上方位缺陷、中間部位缺陷、偏下方缺陷、下邊緣缺陷，模型示意圖如圖4所示，分子動力學模擬結果如圖5所示；第二組為橫向方位缺陷，包括左邊緣缺陷、偏左方位缺陷、中間部位缺陷、偏右方位缺陷、右邊緣缺陷，模型示意圖如圖6所示，分子動力學模擬結果如圖7所示。

圖4 y方向空位缺陷模型

圖5 y方向空位缺陷分子動力學模擬結果

圖6 x方向空位缺陷模型

圖7 x方向空位缺陷分子動力學模擬結果

分別對這兩組不同位置的含缺陷模型施加y方向和x方向的應力，對所得應力-應變進行最小二乘法的直線擬合，求出石墨烯的楊氏模量。縱向方位缺陷和橫向方位缺陷的石墨烯楊氏模量計算結果分別如表3所示。

表3 含缺陷石墨烯楊氏模量的結果

由表3可知，縱向方位含缺陷石墨烯的楊氏模量均小于無缺陷石墨烯楊氏模量。施加y方向應力時，中間位置缺陷石墨烯的楊氏模量值為1 175.42 GPa，小于上下兩邊位置缺陷石墨烯的楊氏模量，這是因為施加應力和缺陷的方向都是縱向的，當施加應力與缺陷的方向相同時，不易造成模型的破壞。此時，缺陷對模型的穩定性影響較小，而中間位置的缺陷對模型穩定性影響相對于上下兩邊位置的缺陷更大；施加x方向應力時，中間位置缺陷石墨烯的楊氏模量值為1 156.20 GPa，大于上下兩邊位置缺陷石墨烯的楊氏模量，這是因為施加應力的方向是橫向的，而缺陷的方向是縱向的，當施加應力方向與缺陷方向垂直時，較易造成模型的破壞。此時，缺陷對模型的穩定性影響較大，而上下兩邊位置的缺陷對模型穩定性影響相對于中間位置的缺陷更大，即上下兩邊緣更容易使得模型破壞。

當所施加的應力方向與缺陷方向相同，缺陷對模型的穩定性影響較小；當所施加的應力方向與缺陷方向垂直，缺陷對模型的穩定性影響則較大。

可見，單空位缺陷的位置對石墨烯楊氏模量有一定的影響，當缺陷對模型穩定性影響較大時，邊緣位置缺陷對于模型穩定性的影響相對于中間位置缺陷更大，即邊緣位置缺陷更容易使模型破壞；當缺陷對模型穩定性影響較小時，邊緣位置缺陷對于模型穩定性的影響相對于中間位置缺陷更小。

3.3 空位缺陷的缺失率對石墨烯力學性能的影響

由于缺陷會對石墨烯的力學性能產生一定的影響，為研究缺失原子的數目和形式對石墨烯性能的影響，設計了兩種類型的空位缺陷，即映射缺陷和隨機缺陷。這里的映射缺陷為多空位缺陷，指的是缺失的位置聚集在一個固定的位置，設計了映射橫向長條狀缺陷、映射縱向長條狀缺陷、映射圓孔狀缺陷。隨機缺陷屬于單空位缺陷，指的是缺失的原子隨機分布在各個位置，所謂的隨機，也就是隨著實驗次數的不同，缺失位置以及實驗結果都不一樣，但由于是隨機的，其結果也會在一定的范圍內波動。

為了更好地說明空位缺陷對石墨烯力學性能的影響，設計并研究了映射缺陷和隨機缺陷的缺失率對其楊氏模量的影響。缺失率Q為

(10)

式(10)中：n為缺失原子的個數；N為完美石墨烯總原子個數。

除了缺陷之外，還考慮石墨烯手性對楊氏模量的影響。如圖8(a)所示，石墨烯的手性由手性矢量[22]C定義，即

C=n1a1+n2a2

(11)

式(11)中：a1、a2為晶胞矢量；n1、n2為整數(n1≤n2)。

根據矢量C或手性角度α，可將石墨烯分為鋸齒型和扶手型。當荷載方向為y方向，手性矢量C與x軸的夾角α=0°，即鋸齒型(Zigzag)，如圖8(b)所示；手性矢量C與x軸的夾角α=30°，即扶手型(Amchair)，如圖8(c)所示。

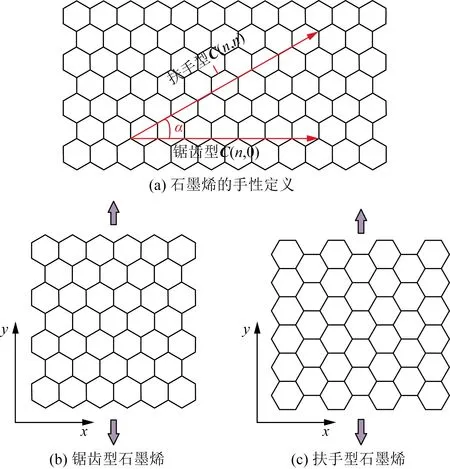
圖8 石墨烯手性示意圖

對各種類型缺陷缺失不同數目原子的模型均進行計算，計算時分別在y和x方向施加應力，并對其應力-應變曲線在應變為0～0.25區間內進行最小二乘法擬合，結果即為石墨烯鋸齒形方向和扶手型方向的楊氏模量。

3.3.1 映射橫向長條狀缺陷

映射橫向長條狀缺陷是由無缺陷石墨烯片的中間位置原子開始，往橫向兩邊方向依次缺失原子，模型示意圖如圖9所示，分子動力學模擬結果如圖10所示。石墨烯片的原子缺失率與楊氏模量的關系如圖11所示。從圖11中可以看出，隨著缺失率的增加，石墨烯的楊氏模量不斷減小，而鋸齒型石墨烯的楊氏模量減小得更明顯，扶手型石墨烯的楊氏模量只是在小范圍內減小。原因是原子是橫向缺失的，當缺失原子數越多，缺陷的形狀就越接近橫向長條狀，此時，施加y方向應力(鋸齒型)，模型就越不穩定，易造成模型的破壞；而施加x方向的應力(扶手型)，對模型的穩定性造成的影響不大。由此可見，對于映射橫向長條狀缺陷，隨著缺失率的增大，石墨烯的楊氏模量不斷減小，并且鋸齒型石墨烯的楊氏模量減小得更快。

圖9 映射橫向長條狀缺陷模型

圖10 映射橫向長條狀缺陷分子動力學模擬結果(扶手型)

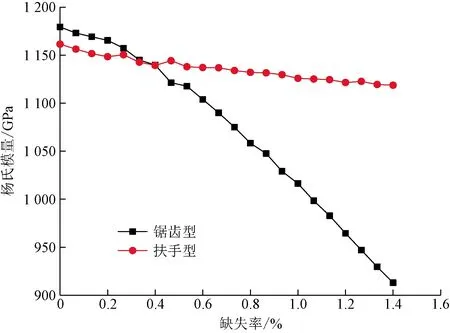
圖11 映射橫向長條狀缺陷石墨烯的缺失率與楊氏模量的關系

3.3.2 映射縱向長條狀缺陷

映射縱向長條狀缺陷是由無缺陷石墨烯片的中間位置原子開始，往縱向兩邊方向依次缺失原子，模型示意圖如圖12所示，分子動力學模擬結果如圖13所示。石墨烯片的原子缺失率與楊氏模量的關系如圖14所示。隨著缺失率的增加，石墨烯的楊氏模量不斷減小，而扶手型石墨烯的楊氏模量減小得更明顯，鋸齒型石墨烯的楊氏模量只是在小范圍內減小。原因是原子是縱向缺失的，當缺失原子數越多，缺陷的形狀就越接近縱向長條狀，此時，施加x方向應力(扶手型)，模型就越不穩定，易造成模型的破壞；而施加y方向的應力(鋸齒型)，對模型的穩定性造成的影響不大。由此可見，對于映射縱向長條狀缺陷，隨著缺失率的增大，其楊氏模量不斷減小，并且扶手型石墨烯的楊氏模量減小得更快。

圖12 映射縱向長條狀缺陷模型

圖13 映射縱向長條狀缺陷分子動力學模擬結果(扶手型)

圖14 映射縱向長條狀缺陷石墨烯的缺失率與楊氏模量的關系

3.3.3 映射圓孔狀缺陷

映射圓孔狀缺陷是由無缺陷石墨烯片的中間位置原子開始，往四周依次缺失原子，缺失原子的部位為圓孔狀，模型示意圖如圖15所示，分子動力學模型如圖16所示。由于缺失原子后的形狀接近圓孔狀，因此缺失的數目并不是固定的。石墨烯片的原子缺失率與楊氏模量的關系如圖17所示。由圖17可知，隨著缺失率的增大，鋸齒型和扶手型石墨烯的楊氏模量均減小，并且鋸齒型的楊氏模量比扶手型的大。

圖15 映射圓孔狀缺陷模型

圖16 映射圓孔狀缺陷分子動力學模擬結果

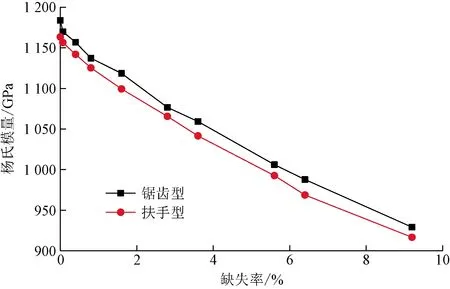
圖17 映射圓孔狀缺陷石墨烯的缺失率與楊氏模量的關系

3.4 隨機缺陷

對于隨機缺陷石墨烯的分子動力學模擬，采用如下步驟進行。

(1)采用MS的腳本進行隨機選取原子的操作，然后將選中的原子刪除，即缺失原子。

(2)由于所選擇的原子是隨機的，因此為了保證結果的隨機性，將隨機選取原子的過程重復進行10次，即對缺失相同原子數的模型重復進行10次隨機選擇，并將選中的原子刪除，即可得出10個缺失相同原子數的不同模型。由于篇幅所限，本文僅給出隨機缺失5個原子的石墨烯模型中的3個模型示意圖，如圖18所示，對應的分子動力學模擬結果如圖19所示。

圖18 隨機缺陷模型

圖19 隨機缺陷分子動力學模擬結果

(3)分別對這10個模型施加y方向和x方向的應力，并進行計算。

(4)將計算得出的應力應變值進行最小二乘法的直線擬合，得出10個楊氏模量的值后，取平均值即為最終的楊氏模量。隨機缺陷石墨烯楊氏模量的誤差棒如圖20所示，根據誤差棒圖示，10個隨機缺陷石墨烯模型的楊氏模量略有波動，相差并不大，鋸齒型石墨烯楊氏模量的值在1 136～1 144 GPa波動，扶手型石墨烯楊氏模量的值在1 120～1 126 GPa波動。

圖20 隨機缺陷石墨烯楊氏模量的誤差棒

圖21為隨機缺陷的缺失率和楊氏模量的關系圖，從圖21中可以看到，隨著缺失率的增加，楊氏模量不斷減小，并且鋸齒型石墨烯的楊氏模量比扶手型的大。

圖21 隨機缺陷石墨烯的缺失率與楊氏模量的關系

4 結論

基于分子動力學方法，采用MS軟件進行模擬，研究了不同類型含缺陷以及原子缺失率對石墨烯楊氏模量的影響。可得出以下結論。

(1)單空位缺陷的位置對石墨烯楊氏模量的影響，由缺陷對模型穩定性的影響決定。當影響較大時，邊緣位置的缺陷對于模型穩定性相對于中間位置的缺陷更大，楊氏模量的值下降更多；反之，當影響較小時，邊緣位置的缺陷對于模型穩定性相對于中間位置的缺陷更小，楊氏模量的值下降更少。

(2)對于映射長條狀缺陷、映射圓孔狀缺陷等不同形狀缺陷的石墨烯，隨著缺失率的增大，楊氏模量均減小。對于隨機缺陷的石墨烯，楊氏模量也隨著缺失率的增加而減小。

(3)對于映射圓孔狀缺陷的石墨烯，鋸齒型石墨烯的楊氏模量總大于扶手型石墨烯的楊氏模量。對于映射橫向長條狀缺陷和映射縱向長條狀缺陷，隨著缺失率的增大，鋸齒型和扶手型的楊氏模量相差較大。當施加應力方向對含缺陷模型的穩定性影響較大時，其楊氏模量減小的幅度就越大，當施加應力方向對含缺陷模型的穩定性影響不大時，其楊氏模量減小的幅度就小。