基于變權重的水庫滑坡穩定性模糊綜合評價
高明,賀可強*,劉洪華,王忠勝,全恩偉
(1.青島理工大學土木工程學院,青島 266400;2.青島地質工程勘察院(青島地質勘查開發局),青島 266100; 3.山東華通路橋工程有限公司,臨沂 276000)
滑坡影響范圍大、治理難度高、危害性強,水庫型滑坡大規模的坡體下滑會堵塞河道、阻礙交通,造成巨大的經濟損失,甚至導致人員傷亡。因此,如何準確確定滑坡所處的穩定性狀態,從而及時預警或采取有效的防治措施,對預防巨大災害的發生至關重要。
中外針對滑坡穩定性的評價主要分為基于假定簡化模型計算的方法和基于統計學、數學的不確定性方法[1-4]。近年來,隨著人們對滑坡非線性的認識,模糊數學綜合評價法作為一種非線性分析方法,以其模型簡單、多層次和定量化的突出優點[5],在滑坡穩定性評估、預測工作中得到了廣泛的應用并不斷發展[6-8]。而在其應用過程中,評價指標的選擇及其權重的確定是研究的難點和重點。Beyabanaki等[9]得出地下水、土體參數、天氣條件等均為滑坡穩定性影響因素指標;朱德明等[10]對金沙江白格滑坡進行野外調查,并結合其實際工程地質條件及殘留體變形特征選取評價指標;李聰等[11]運用層次分析及關聯函數確定指標主客觀權重,并將其賦權得到動態權重;王春燕等[12]通過灰色關聯分析法得到一級模糊綜合評價因素權重值;宋華艷等[13]借助地理信息系統(geographic information system,GIS)空間加權疊加分析技術對評價因子進行分析得到滑坡易發性分級。這些研究都是為了客觀評價滑坡穩定性,減少滑坡穩定性評價結果被主觀因素干擾,合理評價滑坡穩定性,減少事故的發生。
綜上所述,雖然目前存在各種滑坡穩定性狀態評價指標,但由于其結構層次和相互影響程度較為復雜,很難系統地建立它們之間的關聯性[14];此外,常規賦權方法得到的評價結果僅代表評價時滑坡體的穩定性狀態,但隨著其內外部條件的不斷改變,滑坡變形情況也會發生變化,應該將這種情況考慮在評價指標的賦權中,使評價結果隨著變形情況發生動態變化,從而更加符合客觀實際。
鑒于此,現結合水庫型滑坡內、外部條件及相關規范[15-16]規定選擇滑坡穩定性影響因素,基于指標因素間的客觀規律和相關函數,確定各評價指標對穩定性等級的隸屬度,運用層次分析法和專家經驗確定評價指標權重,并結合實際監測數據的變化對權重進行改變,構建模糊綜合評價模型;并以三峽庫區白水河滑坡為例,進行變權重穩定性模糊綜合評價,驗證該方法的可行性,以期為類似滑坡穩定性評價提供科學思路。
1 滑坡穩定性評價指標的選取
影響水庫型滑坡穩定性的因素繁多,關系錯綜復雜,因此,確定科學可靠、系統完整的指標體系是滑坡穩定性評價的前提。滑坡內部因素對坡體穩定性產生直接影響,坡度和坡高會影響坡體滑動面剩余下滑力;巖體物質組成決定了坡體抗外部荷載和人為擾動的能力,不同的組成物質其滲透性也不盡相同,從而影響水徑流與入滲的程度。此外,外部環境條件也會間接影響坡體穩定性,水庫型滑坡受庫水位波動以及降雨等影響較大,其所在地區大部分地表水系較發育,并且受季節性沖溝沖刷的影響,滑坡前緣極易出現錯移的現象。
為了使評價指標體系能全面、準確地反映對滑坡穩定性狀態的影響程度,在指標體系設計時,盡量確保其科學完整、客觀實用,同時將影響程度小的評價指標篩除,避免因素過多而分散主要指標的作用。綜合研究中外典型滑坡穩定性影響因素,結合水庫型滑坡成因和地質水文結構等特征并考慮各指標監測的可操作性,將滑坡穩定性評價指標概括為4項10個因素,如表1所示。

表1 水庫型滑坡穩定性評價指標
2 滑坡穩定性評價模型
基于滑坡監測數據和相關穩定性安全指標等,運用層次分析法將復雜的滑坡穩定性問題的定性和定量因素分層簡化,計算各層次結構的權重;運用模糊綜合原理,將定性因素定量化并進行評價。
2.1 確定穩定性評價指標集和評語集
確定影響效果明顯并且具有代表性的m個指標,分別定義為u1,u2,…,um,則
U={u1,u2,…,um}
(1)
即評價指標集。
確定評價結果等級為n個,分別定義為v1,v2,…,vn,則模糊綜合評價評語集可表示為
V={v1,v2,…,vn}
(2)
2.2 確定隸屬度及模糊關系矩陣
定量評價指標根據數值大小和評價等級分為4個范圍,可統一表示為: (3) (4) (5) (6) 其中,對于數值越大越好的定量指標,采用升半梯形分布隸屬度函數,對于數值越小越好的定量指標,采用降半梯形分布隸屬函數[18]。 運用上述方法,基于評價指標集和評語集,首先確定每個單因素指標隸屬度子集合Ri,進而確定如下形式的模糊關系矩陣: (7) 式(7)中:rij為指標ui隸屬于評價等級vj的程度,取值范圍0~1。 選用的權重不同得到的結論也會完全不同。 2.3.1 應用層次分析法確定初始權重 將復雜的滑坡穩定性評價問題按照元素類別不同分解為目標、準則、指標三個層次,在此基礎上進行分析。 為了提供下層元素對上層元素影響程度的具體可靠數據,采用1~9標度法[19],比較同層元素相對重要性,構成判斷矩陣: (8) 式(8)中:uij>0,表示對于與之相關的上一層元素而言,ui相較于uj的重要性數值;uij=1/uji;uii=1。 采用特征根法計算各元素權重,過程為 (9) (10) 則W=(W1,W2,…,Wm)即屬于同一上級的各評價指標的初始權重向量。 一致性檢驗的計算公式為 (11) 式(11)中: (12) (13) 式中:RI為隨機平均一致性指標,其取值如表2所示;CI為一致性指標;λmax為矩陣的最大特征根;Wi為參與計算指標的初始權重;m為指標數量。如果計算得出CR>0.1,則判斷矩陣不一致,需重新取值;若CR<0.1,則矩陣一致性通過檢驗;當矩陣階數為1和2時,RI=0,此時矩陣不會出現權重分配不一致,自動通過檢驗。 表2 隨機一致性指標RI值 2.3.2 基于評價指標的變動進行變權重 常權重僅表示在理想狀態下各評價因素之間的相對重要性,可能會隱沒較差等級的評價指標對評判結果的影響,而變權重同時還考慮了各因素之間的均衡性,體現了在不同目標等級狀態下各個因素不同的組態變化。為減少確定評價指標初始權重時的主觀因素并避免關鍵性指標被平均化,使用變權理論修正各指標權重,以突顯各指標在評價中的均衡性。 采用懲罰型變權向量[20]: W(x)=[ω1(x),ω2(x),…,ωm(x)] (14) 并采用Hardarmard乘積計算: (15) 式中:W為常權向量,W=(W1,W2,…,Wm);S(x)為狀態變權向量,S(x)=[S1(x),S2(x),…,Sm(x)];選用均衡函數[21]: (16) 由權重向量W與模糊關系矩陣R可得評價結果S為 S=W°R=[W1,W2,…,Wm]° (17) 式(17)中:°為模糊算子。 白水河滑坡位于秭歸縣白水河村,屬于典型的三峽庫區深層堆積層滑坡,毗鄰長江南岸。“靠椅狀”滑坡,整體坡度約30°,南部高北部低,平均厚度大約為30 m,以巖體材料分界,后緣最高處約400 m,坡度約36°;中部由于道路修建等出現多級平臺,較為平緩;前緣135 m以下長期處在江水浸沒中,約120 m高程以下為坡度約29°的陡坎。滑體體積1 260×104m3。滑坡全貌如圖1所示。 圖1 白水河滑坡全貌 根據白水河滑坡地層勘探,第四系殘坡積碎石土和塊石占比較高,粉質黏土所占比例也很大,結構松散,靠近滑面處多為砂巖,孔隙率變化較大,含水性不均勻。下伏基巖主要成分是含碳質粉沙質泥巖,大多數呈現中風化—強風化狀,巖體完整性不同,裂隙高度發育切割巖體。白水河是歷史上頻繁滑動的堆積體順層滑坡,年平均降雨量約982 mm,其滑動和變形大多出現在雨季,主要表現為裂縫、坍塌和下沉。2006—2015年間,每逢雨季,滑坡均會有多條地裂縫出現或發育,呈羽狀或階梯狀,寬約50 mm,延伸超過50 m,滑坡局部出現變形和拉裂坍塌。 將表1元素按屬性不同分為目標層A、準則層B和指標層C,如圖2所示。圖2中指標層各元素即構成了模糊綜合評價指標集U。 圖2 白水河滑坡穩定性評價層次體系 根據《滑坡防治工程勘查規范》[22]中12.4.6條規定確定評語集V,即將滑坡穩定性狀態分為穩定、基本穩定、欠穩定、不穩定4個等級。 根據白水河滑坡工程概況,提取出穩定性評價指標所需要的數據。 選擇有經驗的專家以總分20對定性指標打分,如表3所示,歸一化標準處理后得單指標隸屬度矩陣為 表3 白水河滑坡定性指標專家打分 R3=[0 0.3 0.7 0] (18) R5=[0 0.2 0.2 0.6] (19) R6=[0.1 0.1 0.4 0.4] (20) R8=[0 0.4 0.4 0.2] (21) 定量指標以滑坡平均坡度為例,白水河滑坡平均坡度為29°~34°,根據2.2節隸屬度函數計算公式[式(3)~式(6)],可得平均坡度對穩定性等級的隸屬度為 R1=[0 0.5 0.5 0] (22) 同理可得其他定量指標的隸屬度: R2=[0 0 0 1] (23) R4=[0 0.2 0.8 0] (24) R7=[0.8 0.2 0 0] (25) R9=[0 0 0.5 0.5] (26) R10=[0 0 0 1] (27) 由各指標隸屬度即構成模糊關系矩陣R。 構造各層次子因素之間的比較判斷矩陣。一級指標判斷矩陣為 (28) 基礎指標層各因素判斷矩陣為 (29) (30) (31) (32) 其中,A-B為目標層A對應的下層準則層B;B1-Ci為準則層第一個類型相應的下層指標層各元素,其余同理。 表4 白水河滑坡穩定性評價指標權重 表5 一致性檢驗結果 在滑坡發生變化時,將實際工程監測數據作為動態指標的數據來源。 首先需要合理確定均衡函數變權系數t,取值為0~1,根據相關研究,取t>0.5時更趨向于常權結果,忽視了因素間的平衡關系,而取t<0.5時的結果彌補了這一不足。因此,若保守評價或某個特殊因素對體系安全性影響重大,則取t<0.5,相反取t>0.5。 文獻[23]中將該變權公式應用于儲氣庫艙體穩定性評價中,并取t=0.2計算,取得了良好的評價效果。而滑坡穩定性影響重大,評價應嚴格,偏向保守嚴謹,故選擇t=0.2進行計算,根據式(15)和式(16),結果如表4所示。 將指標層各單指標隸屬度矩陣與其權重向量進行計算,即得準則層因子對評價等級的隸屬向量,以結構特征因素的評價向量為例: =[0 0.312 0.528 0.160] (33) 則準則層各因素的評價向量為 (34) 將RB與相應的權重向量通過加權平均型模糊算子運算可得滑坡穩定性對評語集合的隸屬向量為 S=WB°RB =[0.17 0.12 0.32 0.39]° =[0.088 0.200 0.401 0.311] (35) 根據最大隸屬度原則,從向量矩陣中最大值出 現的位置,可判斷其對應的評語集結果,即白水河滑坡處于欠穩定狀態。 采用變權重向量與隸屬度矩陣進行運算,得出準則層各因素對評語集的隸屬向量為 (36) 則變權重得到的穩定性對評語集合的隸屬向量為 (37) 可得白水河滑坡處于不穩定等級。 依據滑坡的監測數據分析(來源:湖北長江三峽滑坡國家野外科學觀測研究站),在降雨和庫水位波動等的耦合變動作用下,白水河滑坡穩定性稍差,2003年三峽水庫蓄水水位高度達到135 m,坡體出現明顯滑動周界以及滑動面,某些監測點宏觀位移甚至已接近3 m。并且文獻[24]通過試驗與數值模擬也得出的滑坡在庫水位反復波動干擾下會造成失穩情況。本文提出的基于變權重水庫滑坡穩定性模糊綜合評價方法得出的穩定性結果與現場實際情況基本一致,滑坡變為欠穩定狀態。 此外,根據白水河滑坡監測數據,滑坡區的裂縫發育、庫水位升降、年降雨量等都在發生變化,以水位波動及降雨引發的裂縫變形為例:水位于2007年2—7月首次由154 m下降到145 m,滑坡東側和后緣邊界基本貫通,西側裂縫大量展布;2008—2014年,在強降雨的影響下,滑坡局部出現淺層坍滑,裂縫依然存在但未發育;2015年6—7月,降雨頻繁,總降雨量達到約215 mm,白水河滑坡出現了較大宏觀變形,滑坡局部變形速率將近14.60 mm/d[25]。結合3.5節可以得知,分別運用初始權重和變權重進行模糊綜合評價,最終得出了不同的結果,這正顯示了隨著時間的推移,滑坡變形情況發生了變化,而變權后的評價結果隨著變形情況也發生動態變化,更加符合客觀實際。 針對水庫型滑坡的特點,分析了影響滑坡穩定性因素并考慮因素間的關聯性,提取重要因素,構建評價指標體系;提出結合變權重的模糊綜合評價模型,以白水河滑坡為例,進行穩定性綜合評價,進行了實例驗證,并給出防治對策。 (1)研究水庫型滑坡特點,結合理論分析和規范規定,篩選出適合該研究對象的評價指標,分為結構特征、地質構造、變形特征、水文條件4大項,共包含10個因素。 (2)采用定性與定量相結合的方法計算指標隸屬度;運用層次分析原理得出評價指標權重,并根據滑坡特征的變化進行變權重,建立模糊綜合評價模型。 (3)評價結果表明,白水河滑坡穩定性不佳,且變權前后評價結果有欠穩定和不穩定的區別,體現了變權的科學合理,評價結果隨著變形情況發生動態變化,更符合客觀實際。

2.3 確定初始權重并進行變權重






2.4 模糊綜合評判結果
3 白水河滑坡穩定性的變權重模糊綜合評價
3.1 白水河滑坡工程概況

3.2 白水河滑坡評價因子的層次分析

3.3 建立模糊關系矩陣

3.4 確定初始權重及變權重
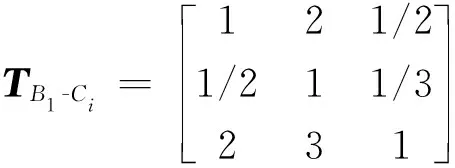




3.5 白水河滑坡穩定性綜合評價


3.6 白水河滑坡穩定性評價結果分析
4 結論

