基于數形結合的小學數學教學探究

毛光團

一、數形結合的相關概述

數形結合，主要指數與形之間的對應關系，其基本概念是指在數學教學中，將抽象的數學語言、數量關系與直觀的位置關系、幾何圖形相結合，將抽象思維與形象思維有效融合，通過以數解形、以形助數的思想形式，將復雜、抽象的問題簡單化、具體化，從而幫助學生快速有效地解決數學問題，提高學生的學習質量與效率。

數形結合的有效應用，可以協助教師通過生動、直觀的圖形，有效激發學生數學學習的主觀能動性，加深學生對數學知識的正確認知與有效理解，并依據圖形特征及規律，提升他們的空間觀念與運算能力，增強數學思維的邏輯性、創造性及開放性，強化數與形的相互轉化能力，從而能夠快速分析并解決數學問題。

二、數形結合在小學數學教學中的應用現狀

（一）缺乏對數形結合思想的正確認知

在實際教學中，部分教師缺乏對數形結合思想的正確認知，致使其在教學中無法充分發揮數形結合的教學價值。一方面，部分教師仍采用題海訓練的方式開展數學知識技能的練習與鞏固，容易降低學生的學習情緒，進而影響學習質量;另一方面，部分教師在應用數形結合思想的過程中，只是單純借助圖形展開數學教學，沒有結合數學規律與圖形特征等強化學生對數形結合思想的有效學習及應用。

（二）學生實際操作較少

當前，仍有少數教師采用傳統的教學觀念，輕視了學生學習的主體性，缺乏知識與技能運用的有效訓練，以及數形結合思想的實際操作。在課堂教學中，學生自己動手實現數與形的轉化會花費較多的時間，為節約教學時間，部分教師會自己作圖，減少學生的實際操作，這對于學生的學習與發展有著一定的限制，不利于學生對知識技能的掌握與運用。

三、基于數形結合的小學數學教學

（一）數學抽象概念的認知教學

在小學數學教學中，數學概念的教學一般是新授課的開始，并貫穿于整個教學階段。數學概念普遍具備較強的抽象性與邏輯性，其中的部分內容是建立在數形結合思想的基礎上。對此，教師應提高自身綜合素養，創新教學方式，在數形結合思想的基礎上開展課堂教學活動，通過圖形與數學概念的結合，幫助學生建立抽象的數學概念與直觀圖形間的轉化關系，提高學生對數學概念的理解程度，強化對數形結合思想的學習與掌握。

例如，在小學階段分數相關知識的教學中，分數的概念、單位“1”的含義、分數單位的意義等是非常重要的概念教學內容，部分認知能力較差的學生無法正確、有效理解分數的相關概念。教師應以數形結合思想為依據，結合教學內容建立抽象概念與直觀圖形間的關系，并結合學生生活實際與學習興趣，將直觀圖形融入課堂教學。授課過程中，教師設置問題：“[34]可以如何表示？”鼓勵學生結合生活實例，并通過繪制圖形理解分數。學生充分發揮想象：假若有20顆糖果，將其平均分為4份，取其中3份即為[34]。同時，學生自主繪圖探究學習。另外，教師還可以通過折疊圖形的方式幫助學生理解分數的意義與性質。教師引導學生將長紙條通過折疊的方式平均分為4份，其中3份涂顏色，涂色部分即為整體的[34]。通過貼近生活的案例和直觀圖形的演示讓學生了解單位“1”可以代表不同的整體，掌握分數的表示形式，理解分數的意義。

（二）解決問題策略的直觀教學

在小學數學中，有許多需要學生具備一定的抽象思維與邏輯推理能力才能解決的數學問題，此時，便需要教師在課堂教學中引導學生借助數形結合思想，使問題中的“數”和“形”統一起來，以形助數、以數輔形，利用直觀的圖形解構復雜抽象的數學問題。

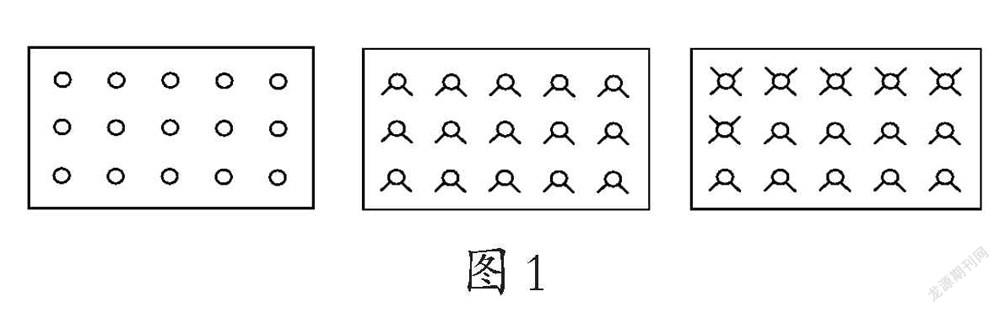
在解決“雞兔同籠”問題的時候，教師便可以充分利用數形結合思想。例題：今有雞兔同籠，上有15個頭，下有42條腿，問雞、兔各幾只？教師可以讓學生圍繞其中的數量關系借助圖形進行探究，教師從旁加以引導：假設15個小圓圈全部都是雞，那么腿的總數就是30條，這樣就會剩下12條腿;再給每只雞分配2條腿，12條腿平均分給6只雞，這些雞就變成了4條腿的兔子;這樣就可以計算出兔子共有12÷（4-2）=6（只），而雞有15-6=9（只）。在這個過程中，教師需要引導學生主動畫圖（如圖1所示）：（1）用方框表示籠子。（2）用15個小圓圈表示15個頭。（3）在每個小圓圈上添上2條腿。（4）再將剩余的12條腿添加上。將解題思路清晰地在圖形上反映出來，幫助學生更好地理解解題過程。

（三）數學運算的創新教學

小學數學中，數學運算是一項重要的教學內容，可以有效提高學生的數學思維與運算能力，為以后的數學學習夯實基礎。小學生探究欲望較強，教師應把握學生的學習興趣，在數學運算的課程教學中創新教學模式，以數形結合思想為教學基礎，以教學內容為學習依據，以學生學科素養發展為教學目標開展小學數學課堂教學，帶領學生建立數量關系的模型，將數學問題轉化為直觀圖形，探究數學運算中的數量關系與應用技巧，同時引導學生靈活運用所學知識解決實際問題，從而提高學生的學習質量，更好地培養學科核心素養。

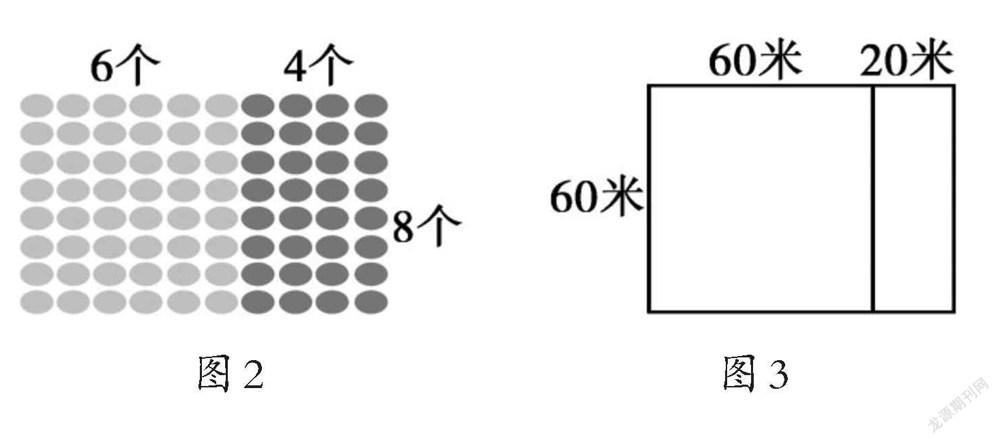
例如，在“乘法分配律”的課堂教學中，教師將數學教學與生活實際相結合，選擇學生感興趣的內容作為新課的導入環節——創設由校園機器人大賽的相關素材構成的趣味情境，從而激發學生的學習熱情與探究興趣。接著由情境圖抽象出點子圖（圖2），借助圖中兩個方陣點子數的和，運用以往所學數學知識幫助學生列出算式：6×8+4×8=（6+4）×8，得到運算律的初步表象。再出示圖3，通過圖形中不同部分的面積關系幫助學生展開深度學習。教師可以進行合理設疑：圖形中的正方形和長方形有何相同點？如何用等式體現？從而加強學生對“共邊”“相同因數”等的數形關聯的理解，強化對相關知識數形特征的感知，為數學知識的檢驗、規律的解釋夯實基礎。在本課教學中，通過對點子圖、面積圖等直觀圖形的合理運用，學生充分發揮了自身的空間想象與表達能力，深入體會數學規律，實現了從實物表征到圖形表征再到語言表征的跨越，形成了全新的數學模型，總結出乘法分配律（a+b）×c=a×c+b×c。

（作者單位：福建省閩清縣城關小學）