巧用數形結合，讓數學教學更有效

陳麗惠

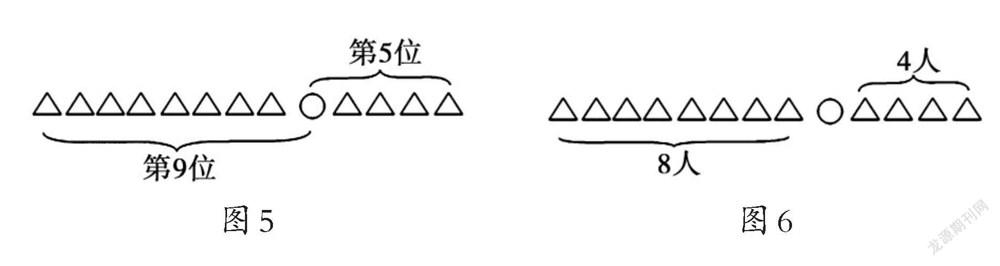
數形結合是一種重要的數學思想，它可以使知識的呈現直觀形象，化繁為簡、化難為易，從而幫助學生掌握知識、發展思維、提高能力。

一、巧用數形結合，讓概念教學更有效

數學概念是現實對象的空間形式和數量關系的本質特征在大腦中的一種反映形式，具有高度的概括性與抽象性。因此，教師要巧用數形結合，借“形”來呈現概念所描述的數學知識，將抽象的文字具體化，讓學生在對“形”的感知中建立表象，從而掌握數學概念的本質特征，構建清晰的數學概念。

教學人教版三上“分數的初步認識”一課。當單位“1”是一些物體時，學生對用分數表示部分與整體的關系感到不適應。教學中，要精心設計教學環節，巧用數形結合讓學生循序漸進地體會到當單位“1”是一些物體時該如何用分數表示整體與部分的關系。

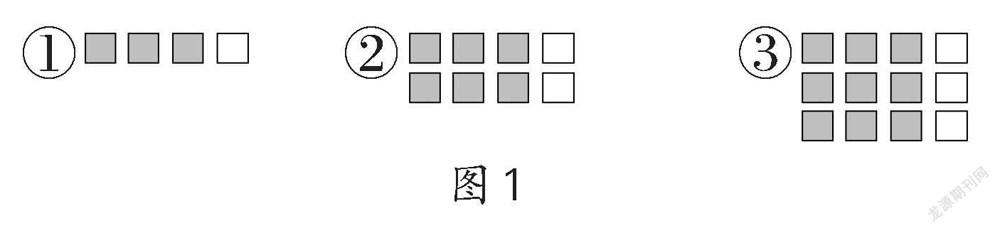
教學例1時，筆者設計用數表示圖中的涂色部分的環節。①出示 ，用幾表示？（用1表示）②出示 ，變成 ，用幾表示？（用3表示）③如果再出現一個該用幾表示？（學生答4后，出示 ，組成 ? ? ? ）

筆者：“用幾表示？”生1：“用3表示。”筆者：“第4個就不算了嗎？”生2：“用[34]表示。”筆者：“有不同想法了，你是怎么想的？”生2：“一共有4個，涂色部分占3個，可以看成平均分成4份，取其中的3份。”筆者：“思路很清晰，解釋很到位。繼續，請用分數表示你看到的涂色部分。”（逐一出示圖1）學生反饋大多為[34]、[68]、[912]。筆者：“有不一樣的嗎？”生3：“我只寫了[34]。我是豎著看的，這樣就都可以看成平均分成4份，取其中的3份，所以都可以用分數[34]來表示。”筆者操作課件，在圖形中加上虛線，將它們平均分成4份，接著說道：“它們都可以用分數[34]來表示。那如果再來一組呢（橫向增加一行方塊），用哪個分數表示？再來10組呢？圖中方塊的數量一直在變，什么不變？”生4：“都平均分成4份，取其中的3份。”筆者隨即指出可以把這些圖形看作“一個整體”。

之后，筆者設計一個核心問題：“6個蘋果”或“[12]張紙”可以看作“一個整體”嗎？一方面幫助學生理解“一個整體”可以很大也可以很小;另一方面引導學生重點思考“分的對象是什么”“平均分成幾份”及“取出幾份”，體會分數部分與整體含義中的關鍵要素，深化對分數本質屬性的認知。

二、巧用數形結合，讓計算教學更有效

教學中，有些教師會側重指導學生掌握計算的方法，卻忽視了對算理的理解，這種教學形式往往無法獲得較好的效果，也難以真正發展學生的數學思維。教學時，教師要巧用直觀圖，把數與形對應起來，引導學生細心觀察，充分交流自己的想法，構建計算方法模型，實現對算理的理解。

教學人教版六上“分數乘分數”一課。學生根據題意列出算式[12]×[15]和[12]×[35]并不困難，對于計算卻無從下手。筆者讓學生拿出一張長方形紙，先折出長方形紙的[12]并涂色，再與同桌分工分別折出[12]張長方形紙的[15]和[35]，并用斜線表示出來。

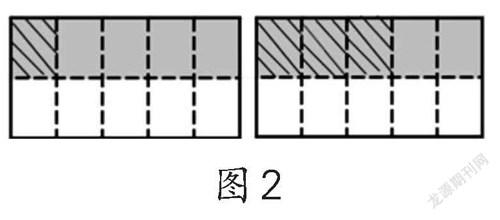
第一層次：觀察圖形，理解

算理（展示學生作品，圖2）。

筆者：“圖中的涂色部分都表示長方形紙的[12]，畫斜線的部分各占[12]的幾分之幾？”生：“畫斜線的部分各占[12]的[15]和[12]的[35]。”筆者：“那[12]的[15]和[12]的[35]又各占這張紙的幾分之幾？小組內討論一下。”在學生回答時，筆者注意引導他們理解并說清“誰是誰的幾分之幾”：[12]的[15]，是以[12]為單位“1”，把它平均分成5份，取其中的1份。但以整張長方形紙為單位“1”進行觀察，就可以發現[12]的[15]占了長方形紙的[110]。這樣，就把幾分之幾乘幾分之幾轉化成1乘幾分之幾了，也就是把[12]的[15]轉化成1的[110]，算理清晰，計算答案也就水落石出了。用同樣思路引導學生理解[12]×[35]=[310]。

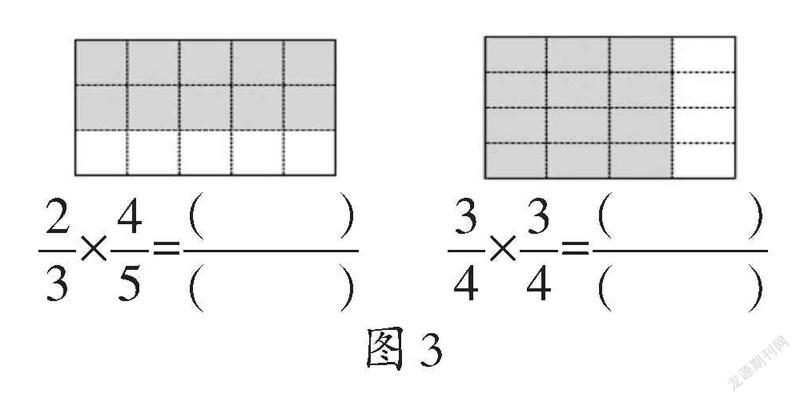
第二層次：根據算式，畫出圖形（學習單與課件

呈現，圖3）。

筆者：“你能在圖中畫斜線表示結果再填空嗎？與同桌說一說‘誰是誰的幾分之幾’。”

第三層次：觀察“數形”，梳理算法。

筆者提出：“經過上面的兩個環節，你有什么發現？”學生小組交流后總結：分數和分數相乘，用分子相乘的積作分子，用分母相乘的積作分母。

通過以上三個層次的數學活動，由簡單到復雜，讓學生在探索和理解分數乘分數算理的基礎上，發現并總結出分數乘分數的計算方法。可見，數形結合的直觀性既可以使學生體會到數學的趣味和奇妙，又可以將枯燥的數學計算變得生動形象，易于理解與掌握，讓課堂教學更有效。

三、巧用數形結合，讓解決問題更有效

在解決問題的教學實踐中，適時巧用數形結合思想，把抽象的問題放在直觀的情境中，幫助學生把復雜的問題簡單化、抽象的問題形象化，學生就能更容易理解各種數量之間的關系，從而提高應用所學知識解決問題的能力。

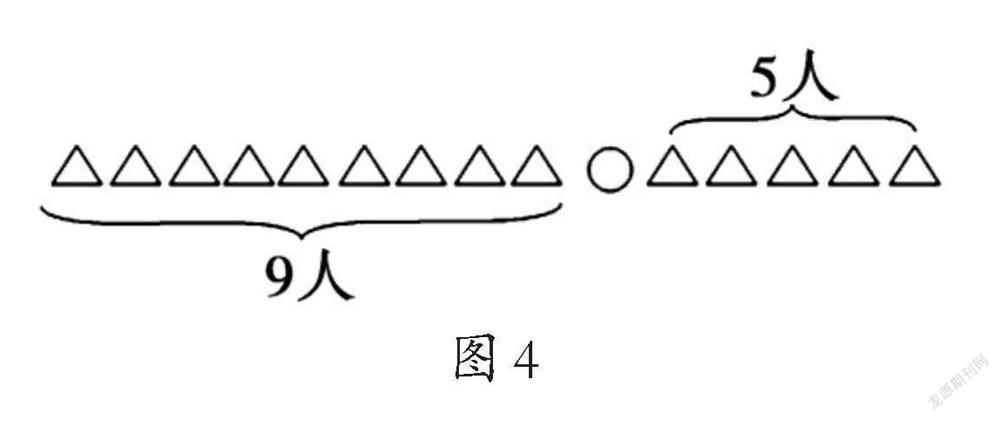
教學人教版一上“排隊問題”。小軍前面有9人，后面有5人，一共有多少人？大部分學生列式9+5=14（人）。筆者：“聽說同學們個個都是畫圖高手，能不能請你們用簡便的圖形把題意表示出來？小組里先討論，再動手畫。”于是就有如下示意圖（圖4）。觀察示意圖后，學生恍然大悟，便修改算式為9+1+5=15（人）。

這時，筆者趁熱打鐵將題目稍微改動：從前往后數，小軍排在第9位，從后往前數，小軍排在第5位，這一隊一共有多少人？有了上一題學習方法的借鑒，學生馬上動手畫示意圖，出現了2種解決方案：9+5-1=13（人），8+4+1=13（人），如圖5、圖6所示。

顯然，借助示意圖來分析題意，形象直觀，既可以幫助學生理解題意和解決問題，又可以讓學生感受到畫圖策略的重要性，是滲透數形結合思想的重要手段之一。在教學過程中，教師要讓學生養成畫圖思考的好習慣，感受數形結合思想的優點，從而提高學生的數形相互轉化能力，實現數形互助互補，提高教學有效性。

（作者單位：福建省廈門市翔安區教師進修學校附屬小學）