BOPPPS教學模式+對分課堂的大學數學課堂教學設計
陳 平 顧 娟 單彩虹
(陸軍裝甲兵學院 北京 100072)
0 引言
在堅持面向世界科技前沿、面向經濟主戰場、面向國家重大需求、面向人民生命健康,深入實施新時代人才強國戰略下,高等教育院校承擔著培育新型人才的重任。而作為高等教育之一的數學教育是培養學生的邏輯和抽象思維能力、幾何直觀能力、空間想象力以及對數學學科的自學能力和實際操作能力等,其教學原則是在教師主導的前提下,發揮學生的主體性原則[1]。作為大學數學基礎課程的《線性代數》《高等數學》《概率論與數理統計》,所包含的教學內容在理工科專業起著重要作用。首先,隨著大數據時代的到來和人工智能技術的發展,當代大部分新學科、新技術都興起與數學和其他學科的交叉,數學思維和方法貫穿了一切科學領域。掌握一定的數學理論和模型,對學生的專業學習和未來發展有一定的影響;其次,大學數學教育旨在培養學生的科學精神、探索創新精神,同時注重將辯證統一的唯物主義精神、無私奉獻的人文主義精神以及艱苦鉆研的科研精神等潛移默化的滲透到課程教學中去。因此,大學數學課程是大學生學習生涯中至關重要的基礎必修課程。
然而,大學數學課程相比初等數學課程課時較少,內容較多,使得以往的課堂教學以教師為主體,授課過程中多以傳統教授為主,重知識講解和邏輯推導,輕實際應用,使學生感到數學課程內容過于抽象,晦澀難懂,更談不上提高學生的創新能力,所以必須轉變教學思想和觀念,以學生為主體,加強學生的數學應用能力,培養高素質有創新的新型人才。因此,將對分課堂和BOPPPS教學模式相結合,改革大學數學課堂教學設計內容,可以有效優化課堂教學效果,提高學生的自學能力,并樹立其數學建模思想,增強學生的應用意識。
1 教學模式概述
BOPPPS教學模式是以建構主義和交際法為理論依據,以有效教學設計著稱,它強調學生作為課堂的主要角色,應全方位參與式學習而不只是聽講;在課堂教學中,教師應及時獲得學生的反饋信息,以調整后續教學活動以期順利達到教學目標。在課堂教學過程中,教師可以借鑒這種模型,充分應用靈活多樣、直觀形象的教學手段,鼓勵學生積極參與教學過程,使學生能深刻地領會和掌握所學知識。它將課堂教學過程分成了六個模塊,分別是導言(Bridge-in)、學習目標(Objective/Outcome)、前測(Pre-assessment)、參與式學習(Participatory Learning)、后測(Post-assessment)和總結(Summary)[7]。
對分課堂[3]是一種新的課堂教學改革模式,它將課堂教學時間分成兩部分。一部分時間以教師講授基本知識、基本概念為主。教師在課堂中著重講授課程重點、難點,但并不將課程內容和盤托出,給學生留白。學生利用另一部分時間進行學習討論。學生通過教師提供的基本內容和課程重難點,根據自己的個人特點和具體情況自行完成內化吸收過程,針對個人情況對教材內容進行全面理解。內化吸收之后,學生回到課堂分組討論自己學過的內容,然后與全班和教師進行深入的互動交流。同一內容,經過教師講授、課后復習、分組討論三個過程分階段學習,理解程度逐步加深。對分課堂將教學過程分為講授(Presenta-tion)、內化吸收(Assimilation)和討論(Discussion)三個模塊,也可簡稱為PAD課堂。
兩種教學模式目的雖然都是促進學生積極參與課堂學習,但是對分課堂的教學模式側重培養學生的學習能力,以及其交流、溝通、發表、見解等能力,而BOPPPS教學模式則重點描述了課堂教學各個環節的流程化體系,使得課堂教學的設計、開發和組織更加條理化、合理化和易操作化。因此將對分課堂和BOPPPS教學模式有效結合,可以有效激發學生主動學習能力以及團隊合作精神,以及提高學生深度學習的水平。
2 基于兩種模式下的“正態分布”課堂教學設計
以《概率論與數理統計》課程中的“正態分布”一節內容為例,將本節課進行對分課堂和BOPPPS教學模式的有效融合,結合幻燈片和計算機軟件等信息資源進行教學設計。
2.1 導言──問題引入
在講授理論知識前,為了吸引學生的注意力和提高學生的學習興趣,首先介紹兩個生動的實際案例,使學生認識到正態分布在實際生活中的普遍性。
引例1是2019-2020秋季學期大二某班學生的某次概率測試成績,如圖1直方圖所示。引例2是對某大學男大學生的身高進行了實際調查,得到了如圖2所示的關于這所大學男生身高的直方圖。讓學生了解到生活中的數據是可以用圖形表示,并對正態隨機變量的存在有感性認識。
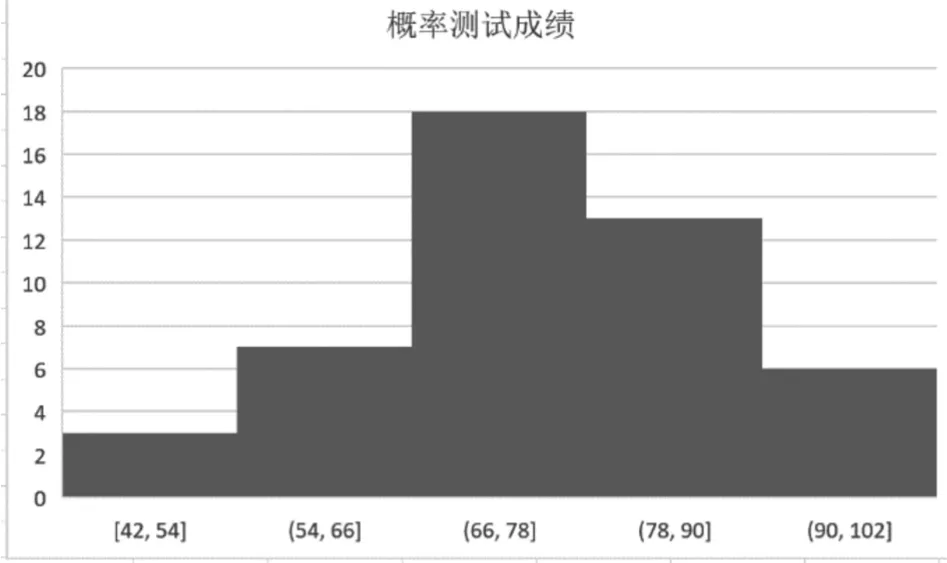
圖1:概率測試成績
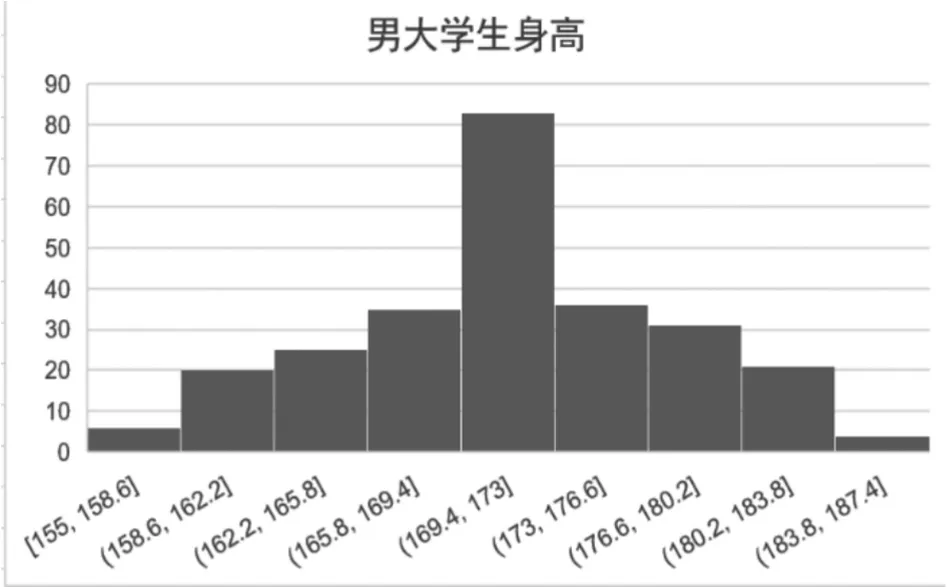
圖2:男大學生身高
2.2 學習目標──對學生的要求
學習目標是讓學生明確是為了讓學生明確本堂課的學習任務,學習完本堂課后應該能做到什么。由于學習目標必須滿足具體、可衡量、可達到以及和其他目標具有相關性等幾個要求,因此,本節課的學習目標設計為以下幾點:
(1)背誦正態分布(標準正態分布)的概率密度,并通過概率密度寫出正態分布(標準正態分布)的分布函數;
(2)對照分布函數的性質,推測標準正態分布函數的性質;
(3)證明正態分布標準化定理;
(4)熟練運用正態分布的標準化定理進行計算。
2.3 前測──問答式
前測的目的是了解學生對本堂課程內容之前所學的相關基礎知識的掌握情況。因此,采用了提問應答的方式給出了兩個問題:分布函數的定義和性質是什么?引例1和引例2中的圖形具有的共同特點是什么?
2.4 參與式學習──自學后進行小組討論
參與式學習的目的在于讓學生主動學習、深入思考、強化印象,要以學生為中心,因此這段時間教師不予講解,提出幾個思考題,先讓學生自學。在自主學習結束后,帶著問題和觀點進行小組討論。討論結束后,將小組的觀點整理成文字形式,選擇一名學生向老師展示學習成果。如果在小組討論過程中,問題得不到解答或者觀點不統一的情況下,可留在答疑環節,由老師統一解答。在參與式學習中,學生可以參考教材、慕課等網課平臺,或者通過互聯網去搜索相關材料。
正態分布的思考題設置如下:
(1)正態分布中兩個參數和的意義是什么?
(2)為什么要討論標準正態分布?它的意義是什么?
(3)如何對正態分布進行計算?
(4)為什么正態分布具有三倍的標準差原則?三倍標準差原則在實際中有哪些應用?
(5)正態分布是由誰發現的?
(6)生活中還有哪些是正態分布?
學生通過小組間分享學習結果,進行歸納總結,對本節內容有了更深刻的理解體會。首先,通過分析圖形進一步掌握以下知識:根據正態分布的概率密度曲線在x趨于無窮時會無限逼近于零,加深了對概率密度規范性這一知識的掌握;通過改變參數的大小,觀察圖形的變化,得出是位置參數,是尺度參數。當固定,改變的大小時,圖形的形狀不變,只是沿x著軸作平移變換;當固定,改變的大小時,圖形的對稱軸不變,而形狀在改變。越小,圖形越高越瘦,越大,圖形越矮越胖。其次,正態分布在求分布函數時比較復雜,而標準正態分布分布函數可查表得到,因此將正態分布標準化后,可得到標準正態分布進行計算。第三,隨機變量的取值幾乎都落在這個范圍內,這在統計學上稱為三倍標準差原則。它的應用是六西格瑪標準,其主要依據之一為正態分布。這個標準是20世紀80年代由摩托羅拉公司提出的概念和相應的管理體系,并全力應用到公司的各個方面,從開始實施的1986年到1999年,公司平均每年提高生產率12.3%,不良率只有以前的1/20,大大提高了企業業績與競爭力。第四,法國數學家棣莫弗最早發現了正態分布的密度形式,由德國數學家高斯加以推廣,正態分布的密度才以概率分布的身份引起人們的重視,因此正態分布也稱為高斯分布。第五,正態分布是日常生活中最常見的也是最重要的一種分布。像學習成績、測量誤差、身高、體重、零件尺寸等都近似服從正態分布。
2.5 后測──課堂練習
后測是用來評估學生學習結果、檢視學生是否完成學習目標。本節課主要采用了案例求解的形式進行測試學生學習成果。
案例1坦克駕駛室高度的設計。
問題提出:坦克是現代陸上作戰的主要武器,有“陸戰之王”之美稱,它是一種具有強大的直射火力、高度越野機動性和很強的裝甲防護力的履帶式裝甲戰斗車輛。由于坦克內部配有武器系統、通信設備、三防裝置等裝置和設備,空間比較狹小,所以對于駕駛人員的身高也是有要求的,盡量不需要太高,也不能太矮,否則影響士兵對道路情況的判斷。為此需要設計駕駛室的最低高度。人的身高服從,根據統計資料,對于中國人,=1.75,2=0.05。現要求艙內不能筆直坐姿的人不超過5%,問駕駛室至少需要多高?
在解答過程中,需要學生運用建模的思維方式解決此問題。需要考慮到在座位是固定的前提下,將問題轉化為求士兵坐姿時從臀部到頭頂的高度。可根據已知和黃金分割點求得從臀部到頭頂滿足要求的最小高度,加上座位的高度即為駕駛室的高度。本題的理論基礎是正態分布的隨機變量落入一區間概率的計算方法。先進行標準化,轉化為標準正態分布后,通過查表即可獲得相關概率。
模型建立:設駕駛室高度為h,士兵坐姿時從座位到頭頂的高度為X,則X~N(1.75×0.382,0.052)=N(0.6685,0.052)(0.618位黃金分割點)。
根據題意
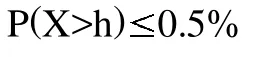
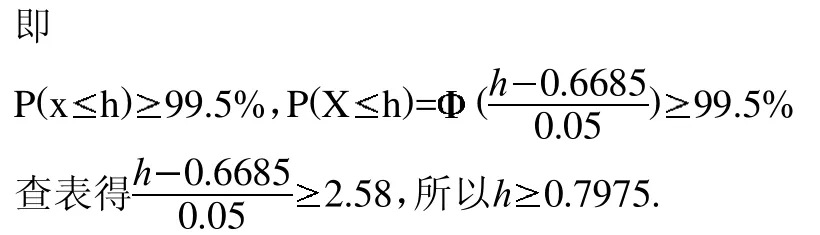
若座位高0.35cm,則駕駛室高度設計為1.1475米即可。
在此過程中可以要求學生運用計算機軟件進行輔助計算。軟件實現:可通過尋找標準正態分布的(下)0.995的分位點來實現,在Matlab軟件中相關命令為norminv(p,mu,sigma)。第一個參數為正態分布的(下)p分位點的概率p,即P{Z 在Matlab命令窗口中編寫命令: 案例2如何預測大學研究生考試中錄取分數線及能否被錄取。 問題提出:報考研究生考試,考生最關心的問題是:自己能否達到最低錄取分數線?自己的考試名次如何?能否被錄取?假設某大學2010年研究生招生準備錄取160人,其中計劃內110人,計劃外50人,實際報考人數為630。考試滿分500分,考后不久通過查分系統得到如下信息:考試平均成績是230分,390分以上的考生有30名。某考生的成績為301分,問他能否被錄取?若被錄取,能否是計劃內學生? 問題分析:此問題即要求預測此次考試的最低錄取分數線,以及這名考生的排名。一般的,成績服從正態分布N(230,2),可以用樣本均值230作為的估計,利用統計量和樣本信息估計出,從而總體的分布確定后可討論其他問題。 模型建立:先預測最低錄取分數線.記最低錄取分數為x0,設考生成績為X,對一次成功的考試來說,X應服從正態分布,即X~N(230,2), 因為最低錄取分數線x0的確定應使高于此線的考生的頻率高于,即, 即最低錄取分數線是294分。 下面預測考生A的名次,其考分x=301, 這表示成績高于考生A的人數約占總人數的26%。即考生A大約排在130名,結論是考生A能被錄取,但他排在110名之后,所以錄取為計劃內學生的可能性不大。 軟件實現:此問題的關鍵是計算標準正態分布的分位點,可利用Matlab軟件中norminv(p,mu,sigma)命令。第一個參數為正態分布的(下)p分位點的概率p,即P(Z 總結是引導學生對于本堂課程內容進行回顧和梳理,找出重點和難點內容加強理解、記憶的過程,因此教師先對本節課內容進行小結,然后提出問題,要求學生課下解決。設置問題為兩個正態分布的隨機變量還是正態分布嗎?為什么?需要滿足什么條件? 本次課堂教學設計以BOPPPS教學模式為主,將對分課堂融入參與式教學環節,兩者有效結合。教師通過生活中的案例引起學生興趣,給出明確的學習目標,讓學生對本節內容有個初步了解。然后提出問題,加大學生的參與力度。通過查詢資料和小組討論進行自主學習,提高學生的中心地位,使學生在興趣驅動下自覺積極的投入到課堂學習中,獲得理想的學習效果。通過案例求解,建立數學模型,并運用計算機軟件進行求解,鍛煉了學生的動手操作能力,并通過課后思考題對學生知識進行拓展。在教學過程中,不應拘泥于某種特定的教學模式,將多種教學方法結合并靈活運用,為培養具有創新意識和創新能力的新型人才起到積極的推動作用。
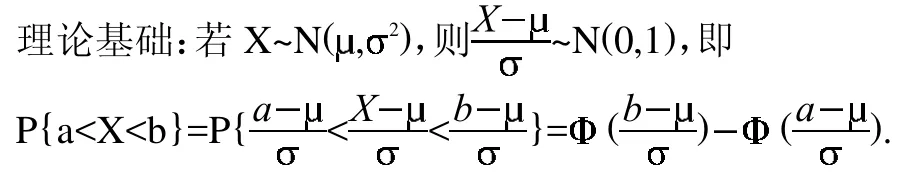
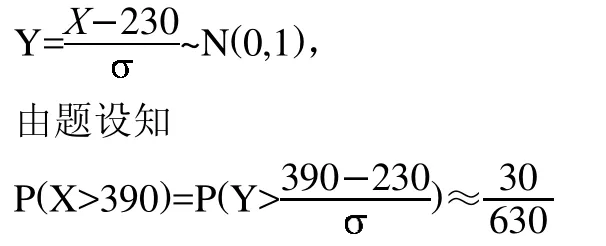
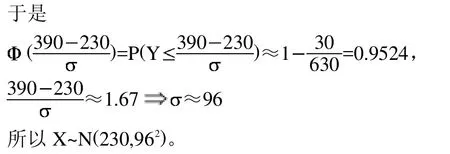
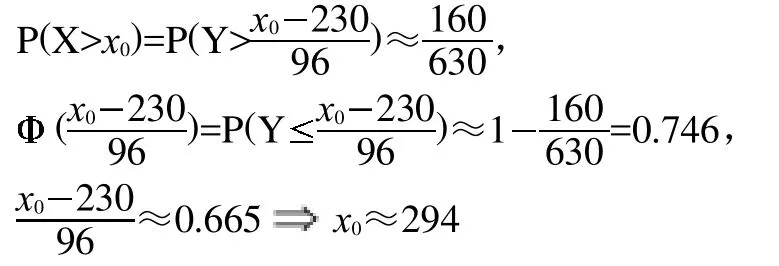
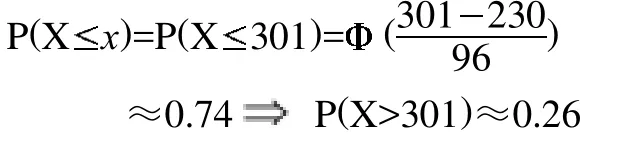
2.6 總結──小結加思考題
3 結論

