利用圖靈測試思維探究非均質數字骰子與真實骰子的區分度

曾子珉 吳俊杰 蘇一

隨著計算機的誕生，計算開始成為人類生活生產、各級各類教育中的一個重要元素，代表運用人腦及電腦進行思維的延伸。圖靈原理試圖說明，計算機可以在一定的數據精度層面仿真真實世界的現象，反過來，人的認知過程就是計算。[1]那么，真實世界、數字世界是否可以等價？在什么條件、多大程度上可以看作不可區分？在均質骰子實驗基礎上，本文利用“圖靈測試”思維，給出非均質骰子的實驗設計與數據分析，以探究這一問題。

● 實驗設計

實驗首先利用3D打印設計制作非均質骰子，并計算擲一次骰子各個面朝下的理論概率。接著，分別進行1000組數字骰子實驗、10000組數字骰子實驗和1000組真實骰子實驗，分析三組數據和理論值之間的關系，初步得出數字骰子模擬真實骰子的效果。最后，借鑒“圖靈測試”思維，引入第三方的“人”，同時分別與數字骰子和真實骰子進行測試，若通過率一致，則認為兩者不可區分。

● 非均質骰子的理論模型、數字實驗和實物實驗

1.非均質骰子的理論概率

根據文獻[2]，將擲骰子看作剛體自由下落然后與桌面碰撞的剛體動力學過程，假設非均質六面體的幾何中心位于點O處、質心位于點M處，MN與棱長a的比值為h，如圖1所示，則在統計學意義上，擲骰子后面EFGH朝下的概率為：

在本案例中，基于3D打印技術設計了非均質三層式骰子，如下頁圖2所示。每一層尺寸均為15mm×15mm×5mm，從上往下每一層的質量為0.5g、0.5g、1.2g，在每一層均勻分布，兩個分界面間的膠重按0.05g計算，總質量為2.3g。在誤差允許范圍內，認為質心在z軸上，以幾何中心O為原點，計算出該模型質心位置：

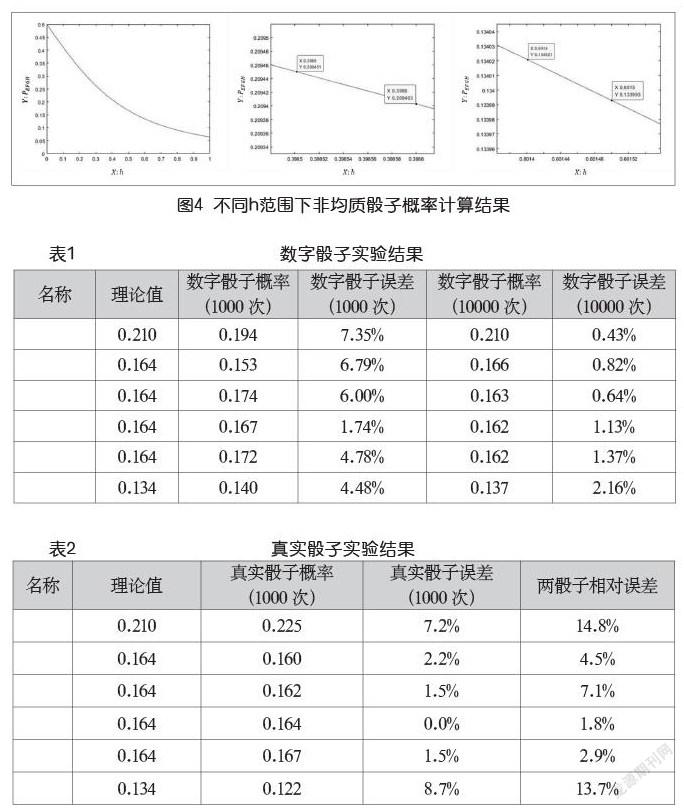
如下頁圖3、圖4所示，將（3）代入（1），利用Matlab可得出面EFGH朝下的概率P1=PEFGH=0.2094。同理，ABCD面朝下所對應的質心r^'=1.52mm，h^'=0.6014≈0.6，〖P_6=P〗_ABCD=0.1340。其余四面朝下的概率

2.數字骰子

為了賦予隨機數以不同概率的意義，首先利用計算機（mind+）在[1，1000]范圍內隨機輸出整數，并進行簡單“編碼”：將P1定義為“輸出的隨機數屬于[1，210]范圍”，同理，P2對應的范圍為[211，374]，P3對應[375，538]，P4對應[539，702]，P5對應[703，866]，P6對應[867，1000]。在處理數據時，先在Excel中利用IF函數劃分6個等級，之后利用COUNTIF函數進行各范圍出現的頻數。

由于數字骰子可以在極短的時間內完成上萬次實驗，所以分兩組實驗，第一組循環輸出隨機數1000次，第二組循環輸出隨機數10000次，利用絕對誤差除以理論值得到相對誤差，結果如表1所示。可以發現，當循環次數增大10倍后，概率誤差明顯降低，服從統計規律。

3.真實骰子

手動投擲3D打印后的非均質骰子1000次，隨機選擇骰子的初始朝向，保證骰子進行自由落體運動，記錄各面朝下的次數，并利用“絕對誤差/均值”計算真實骰子和數字骰子之間的相對誤差，結果如表2所示。可以發現，真實骰子的P2、P3、P4、P5接近理論值，較數字骰子表現更好，而P1、P6較數字骰子表現持平或更差。在1000次實驗條件下，真實骰子和數字骰子相對誤差平均值為7.5%，計算機模擬非均質骰子效果不佳;而在10000次實驗條件下，數字骰子的實驗值和理論值相對誤差降低為1.1%。因此，當實驗次數越多、越符合統計規律時，數字骰子替代真實骰子的可能性越高。

● 非等概率事件下的“圖靈測試”

在上一部分的分析中，數字骰子和真實骰子的實驗是分開進行的，為了進一步探討“非均質數字骰子和真實骰子是否不可區分”，現引入第三方的“人”作為橋梁進行測試。如下頁圖5所示，借鑒“圖靈測試”思維，讓一個人隨機猜測一個1～6之間的隨機數，然后同時分開進行數字骰子和真實骰子實驗，若與人的猜測數字一致，則認為通過“提問”，若最后兩組骰子的通過率一致，則認為數字骰子和真實骰子不可區分。

實驗數據表明，當進行200輪測試時，數字骰子和真實骰子的通過率分別是18%、11%，相對誤差為48.3%;而當進行1000輪測試時，通過率分別為16.8%、19%，相對誤差為12.3%。這說明，當統計規律明顯時，數字骰子和真實骰子的區別越不容易被檢測出來，數字骰子替代真實骰子的可能性越高。

● 總結

在本實驗中，在利用非均質數字骰子和真實骰子分別實驗時，在1000組實驗次數條件下，真實骰子實驗值與理論值更接近，當增大實驗次數時，計算機模擬非均質骰子效果更佳。在引入第三方的“人”進行同時分別測試時，在200組實驗次數條件下，數字骰子和真實骰子的通過率差異較大，容易區分開，而當實驗次數增大到1000時，兩通過率差異控制在15%以內，較難區分開，在此基礎上合理外推，當增大各組實驗、測試次數時，非均質數字骰子和真實骰子的區分度將進一步縮小。當然，本實驗由于現有3D打印工藝的局限性，存在特定填充率下填充結構不可變及無法一體成型打印實驗所需非均勻立方體的情況，分割面粘膠等因素也會導致產生關于z軸分布不均勻的現象，但考慮其重量對整體的影響是可忽略的，故將其歸結于誤差范圍內。

類似地，一方面，在創客教育中，可通過質量的非均勻分布進行任務驅動，讓學生理解質心概念，并深入挖掘3D打印機的精度、填充率、支撐結構、外層結構等因素對質量分布的影響，嘗試調參，有條件的還可以進行更精確的配重;另一方面，在信息技術教育中，也可以通過計算機編程模擬真實世界或人的行為，通過理論計算或統計規律分析等手段，利用圖靈測試的思維，探討計算機仿真的界限，培養學生的計算思維和虛實融合世界觀。

參考文獻：

[1]高新民，羅巖超.“圖靈測試”與人工智能元問題探微[J].江漢論壇，2021（01）：56-64.

[2]施衛平，耿愛芳.骰子中灌鉛對擲骰子結果的影響[J].力學與實踐，2003，25（03）：57-58.

[3]吳俊杰.2022，人工智能、數字人和圖靈原理[J].中國信息技術教育，2022（01）：13.

[4]吳俊杰.構建基于模擬的世界觀：圖靈原理回望[J].中國信息技術教育，2022（01）：79-81.