用平面幾何基本圖形解決與圓相關的綜合問題

李鴻

（福州教育學院附屬中學，福建 福州 350013）

幾何綜合題在初中數學水平考試評價中是常見的一類評價試題，它常以基本圖形為載體，考查學生對問題形成的過程、思維方式、思維水平、對相關知識方法理解的深度以及能否用恰當的數學語言有條理地數學表達的數學思考等。［1］那么如何從綜合問題的復雜圖形中拆解出基本幾何圖形，這是解決幾何綜合題的關鍵，這需要掌握好基本幾何圖形的識圖與構圖。教師在教學中需要重視對幾何基本圖形的教學研究，讓學生認識幾何基本圖形的特征，學會靈活運用基本幾何圖形，化繁為簡地解決復雜幾何圖形綜合問題。

一、復雜圖形構建的綜合問題

（一）以圓與直線型幾何圖形結合的綜合問題

1.由圓與直線組合構建的復雜幾何圖形綜合問題，圖形的復雜需要學生學會把組合的圖形變單一基本幾何圖形的來解決綜合性問題，提升學生的分析問題與解決問題的能力。［2］

2.復雜圖形中基本幾何圖形的隱蔽性，外顯變成內隱，問題解決意在評價學生對基本幾何圖形的認識與理解的水平層次，是否具備創造性解決問題思維水平。

比如圓與直線型幾何圖形結合時，原圖中并不出現圓，而是以其他直線型幾何圖形特征的存在直觀想象隱藏圓的存在，需將隱藏圓還原出來。而有的直線型幾何圖形的基本模型隱去一部分圖形，使得圖形并不完整，需要進行構圖，將基本模型還原。

3.增加圖形的抽象型、新穎度以及可能型，這類問題在于考查學生的抽象概括能力以及知識的應用遷移能力與思維的嚴謹性。［3］

例1：如圖1，四邊形ABCD 內接于⊙O，AB=AC，AC⊥BD，垂足為E，點F 在BD 的延長線上，且DF=DC，連接AF、CF.

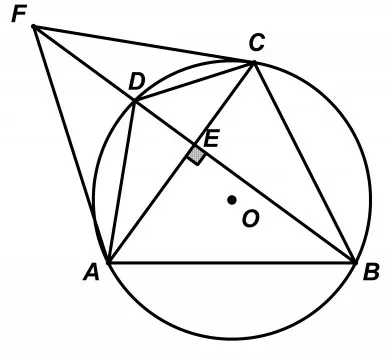
圖1

（1）求證：∠BAC=2∠CAD；

解析：第（1）問實際上是圓自身的“弧、弦、圓心角、圓周角”之間的基本性質的AB 綜合應用。由條件“AB=AC”可得因此∠ABC=∠ACB.而在△ABC 中，由三角形內角和等于180°可得，；由條件“AC⊥BD，垂足為E”可得，在Rt△ABC 中，∠ADB=90°－∠CAD；從而∠BAC=2∠CAD。

第（2）問實際上是由幾個常用的直線型幾何模型組合而成。如圖2（1）是軸對稱模型，由條件“DF=DC”可得∠BDC=2 ∠CFD，結合（1）的結論∠BAC=2∠CAD 以及∠BDC=∠BAC，∠CAD=∠CBD，可得∠CFD=∠CBD，又因為“AC⊥BD，垂足為E”，所以AC 垂直平分BF，因此AC=AB=AF=10；如圖2（3）是雙直角共邊直角三角形模型，應用勾股定理建立方程102-AE2=，解得AE=6，所以CE=4，再在Rt△ABE 中用勾股定理求得BE=8；如圖2（3）是“X”型相似模型，可得，解得DE=3，所以BD=11；如圖2（4）是三角形的等積模型，可得AB·DH=BD·AE，即：10×DH=11×6，解得再在Rt△ADH 中用勾股定理求得所以

圖2 （1）

圖2 （2）

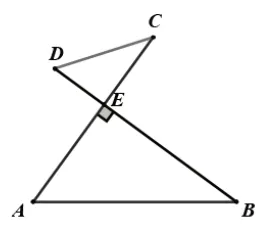
圖2 （3）

圖2 （4）

（二）圓的性質綜合應用的問題

圓相關知識綜合應用的考查是中考數學中的一個重要內容，圓作為一個考查學生直觀想象、邏輯推理、數學建模等核心素養的載體，除了上述常與直線形幾何圖形結合的考查外，常見的題目命制用到的重要性質及技法有：①運用圓是軸對稱圖形也是中心對稱圖形可以對相關結論作合理的猜測；②利用垂徑定理，通過在由半弦、半徑、弦心距組合成的直角三角形，運用勾股定理或銳角三角函數進行計算；③在同圓或等圓中，圓心角、弧、弦、弦心距等量對等量關系，可以轉化相等關系；④由直徑所對的圓周角是直角構造直角三角形以及與扇形面積有關的證明與計算也是圓的綜合題中的另一個熱點題型，求與圓有關的陰影部分的面積時，常常是通過把不規則圖形的面積，用扇形的面積和三角形的面積的和差來解決。

例2：如圖3，O 是Rt△ABC 斜邊BC 邊上一點，以O 為圓心的半圓與三角形的兩直角邊AB、AC 分別相切于D、E 兩點，連接OD.已知AD=3，OB=

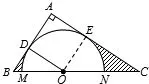
圖3

求：（1）sin∠C；（2）圖中兩部分陰影面積的和.

解析：本題第（1）問的命題背景是圓切線性質的應用，由條件“以O 為圓心的半圓分別與AB、AC 邊相切于D、E 兩點”，應用圓切線的性質，連接OE 后，圖中出現了Rt△COE，Rt△BAC，Rt△BOD，結合OD=OE，得到正方形ADOE，所以OD∥AC，OD=AD=3，所以∠BOD=∠C，所以在Rt△BOD 中，

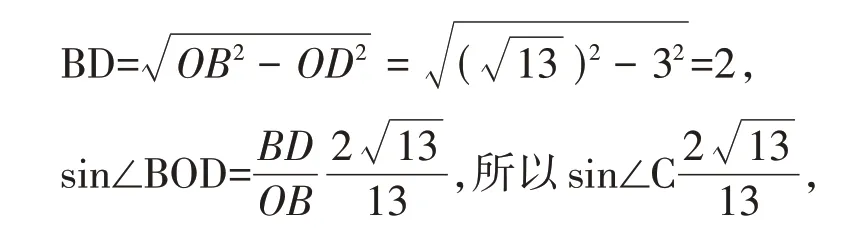
第（2）問是與圓有關的陰影部分的面積計算的考查，把不規則圖形的面積計算轉化為規則圖形的和差運算，S陰影=S△BOD+S△COE-（S扇形DOM+S扇形EON），結合（1）中得到的結論便可進行運算。

二、基本幾何圖形的應用

（一）應用圓的基本性質構造常用的基本幾何圖形

1.如圖4，基于垂徑定理，涉及圓中有關弦長、半徑、弦心距的計算問題大都過圓心作弦的垂線段，構造直角三角形。

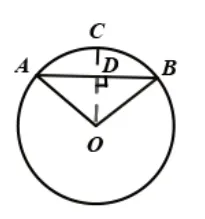
圖4

2.如圖5，基于定理“直徑所對的圓周角是90°”，已知直徑，大都連接圓中的一些線段與直徑構造直角三角形。

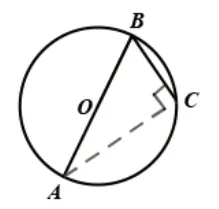
圖5

3.如圖6，基于切線的性質定理，遇到直線與圓相切，常常連接圓心與切點，利用切線的性質得到垂直，再利用直角三角形的性質來解決問題.

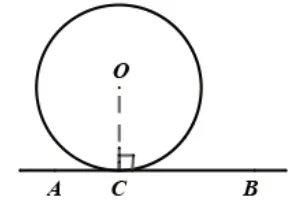
圖6

4.如圖7，基于三角函數概念的應用，在圓中可得到一個常用的結論：一條圓的弦長，及它所對的圓周角度數，直徑這三者的數量關系是：弦長=直徑˙sin（弦所對的圓周角）。由此建立一個意識：圓中的弦長、直徑、弦所對的圓周角，這三個量中已知兩個，第三個量一定可解。

圖7

（二）語言的轉化，還原圖形生成的過程

用好數學的文字語言、符號語言和圖形語言的轉化，還原圖形的生成過程或便可從中分離出基本圖形，理解圖形的內在結構。

例3：如圖8，在平面直角坐標系xOy 中，P 是直線y=2 上的一個動點，⊙P的半徑為1，直線OQ 切⊙P于點Q，則線段OQ 的最小值為______.

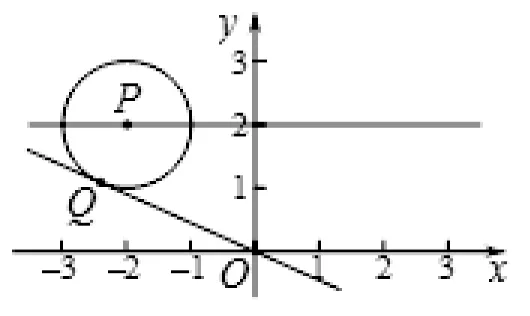
圖8

解析：由條件“直線OQ 切⊙P于點Q”可得到PQ⊥OQ，由“P 是直線y=2 上的一個動點，⊙P的半徑為1”可得到⊙P是一個半徑確定，圓心運動的圓，那么由這兩個條件的符號語言結合圖形語言可轉化為文字語言理解為“直角三角形OPQ 中，邊PQ=1 是確定的，點P 是主動點，點Q 是被動點，那么根據勾股定 理 知，在Rt△OPQ中，OQ=，那么線段OQ 的長度大小由OP 決定，OP最小則OQ 最小”，這樣通過文字語言的轉化理解題意后，把問題轉化為“垂線段最短”的公理的模型應用，當OP 垂直于直線y=2 時候，線段OP 長度最小為2，那么本題得到解決。

（三）以基本幾何圖形為主結構，補全構圖，激活核心條件

引導學生關注基本幾何圖形結構特征，激活問題中的核心條件。從題目顯性條件的基礎上，挖掘題目的隱性條件，在問題“核心條件”的激活上思考，通過添加輔助線，補全構圖，以達到目標問題的順利解決。

例4：如圖9，⊙O 為等邊△ABC 的外接圓，半徑為2，點D 在劣弧AB 上運動(不與點A，B 重合)，連接DA，DB，DC.探究四邊形ADBC 的面積S 是線段DC的長x 的函數嗎？如果是，求出函數解析式；如果不是，請說明理由；

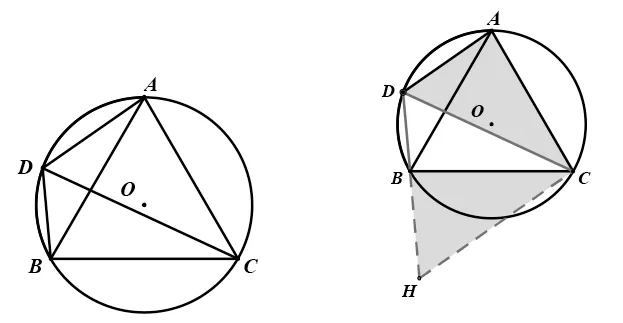
圖9

解析：本題激活核心條件“等邊△ABC”，如圖10，補全手拉手模型的構圖：延長DB 至H，使得DH=DC，連接CH,結合∠BDC=∠BAC=60°□等邊△DHC，結合等邊△ABC,構圖了手拉手模型□△ADC≌△BHC □四 邊 形ADBC的 面 積S=S△ADC+S△BDC=

（四）復雜圖形分解為基本幾何圖形的基本思路

復雜的圓幾何綜合題通常是由圓與直線型、圓與圓型的幾何圖形的組合，使得圖形復雜化，應用轉化的數學思想，把復雜的圖形拆解成基本幾何圖形，還原圖形原來的模樣。

例5：已知四邊形ABCD 是⊙O 的內接四邊形，AC是⊙O 的直徑，DE⊥AB，垂足為E,延長DE 交⊙O 于點F，延長DC，FB 交于點P，如圖11（1），求證：PC=PB,（2）過點B 作BG⊥AD，垂足為G，BG 交DE 于點H，且點O 和點A 都在DE 的左側，如圖11（2），若AB=DH=1，∠OHD=80°，求∠BDE 的大小.

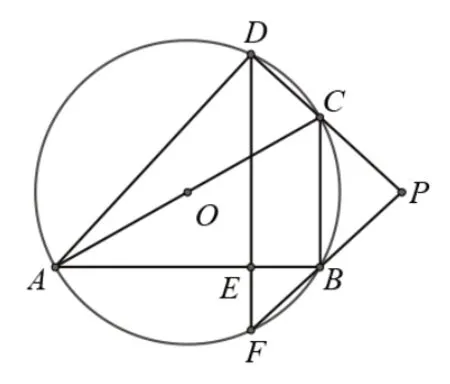
圖11 （1）

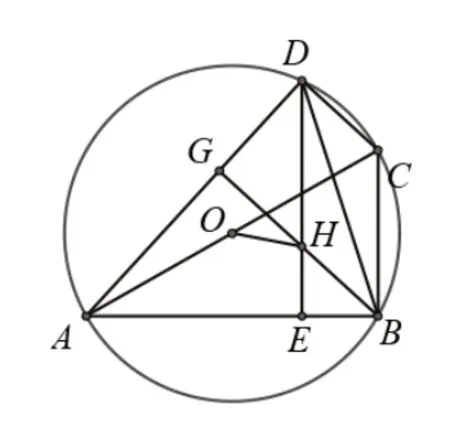
圖11 （2）

解析：本題第（1）問只需從題目條件從原圖中分離出以下幾個基本圖形：

從條件“四邊形ABCD 是⊙O 的內接四邊形”中分離出圖12（1）可推得∠BAD=∠PCB,

從條件“AC 是⊙O 的直徑”中分離出圖12（2）可推得∠CBA=∠CDA=90°，

從定理“同弧所對的圓周角是90°”中分離出圖12（3）可推得∠DAB=∠F，

從條件“DE⊥AB”以及∠CBA=90°中分離出圖12（4）可推得∠CBP=∠F

從以上分離出的四個基本圖形及其得到的結論可得到∠CBP=∠PCB,從而PC=PB.

本題第（2）問從題目條件和原圖中分離出以下幾個基本圖形可以得到順利解決：

從條件“BG⊥AD”結合第（1）的證明過程得到的∠ADC=90°，可得到BH∥DC，由（1）已證BC∥DH，故分離出圖12（5），四邊形DHBC 是平行四邊形，設DH與OC 交予N 點，則∠ONH=∠ACB=60°，∠BDE=∠DBC,從條件“AB=，DH=1”結合第（1）問的證明過程得到的∠ABC=90°，可得到AC=2，即⊙O 的半徑=1，故分離出圖12（6）,可得到長度等于半徑的線段有OD=OA=OC=BC=DH，從圖（6）得到的結論可分離出圖12（7）和12（8）可得到等腰△ODH 和等腰△OAD,從條件∠OHD=80°結合圖12（7）得到的結論可得到∠ODH=20°，再結合已得到的結論“∠ONH=60°”可得到∠DOC=40°，結合圖12（8）得到的結論可得到∠ADO=20°，結合從原圖中分離出的圖12（9）得到的∠ADB=∠ACB=60°可得到∠BDE=∠ADB－∠ADO－∠ODH=20°，故問題（2）得到解決。

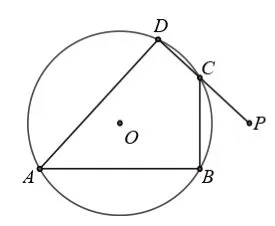
圖12 （1）

圖12 （2）

圖12 （3）

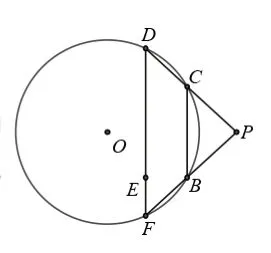
圖12 （4）

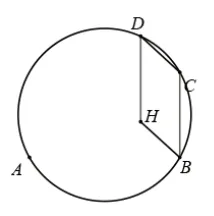
圖12 （5）

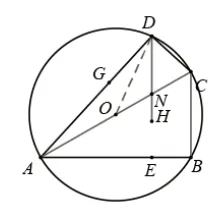
圖12 （6）

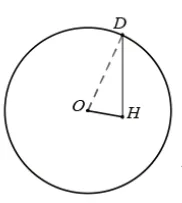
圖12 （7）

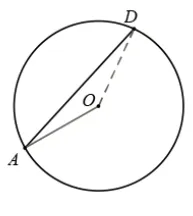
圖12 （8）

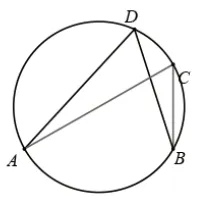
圖12 （9）

（五）隱藏圓的應用

1.如圖13，根據圓的定義構造圓，圓，一中同長也——《墨子·經上》

圖13

2.常見的“四點共圓”基本模型

如圖14，在中考題中涉及的“四點共圓”就是共斜邊且異側雙直角與同側雙直角模型

圖14

例6：如圖15，以直角△ABC 的斜邊BC 為邊在△ABC 的同側作正方形BCEF,設正方形的中心為點O，連接AO，如果AB=4,AO=，則AC=

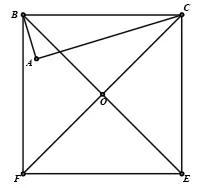
圖15

解析：本題由條件可得，∠BAC=90°，∠BOC=90°，這就構成了以BC 為公共斜邊的同側雙直角模型可推得點B、A、O、C 四點共圓，可得到∠OAC=∠OBC=45°，所以∠BAD=45°，所以△ABD 和△ACG 是等腰直角三角形，結合條件AB=4，可得到，再結合條件，得 到，由“K 形圖”結合OB=OA，可推得△ADO≌△OCG，所以CG=OD=由已得到的△ACG 是等腰直角三角形可得到AC=16.

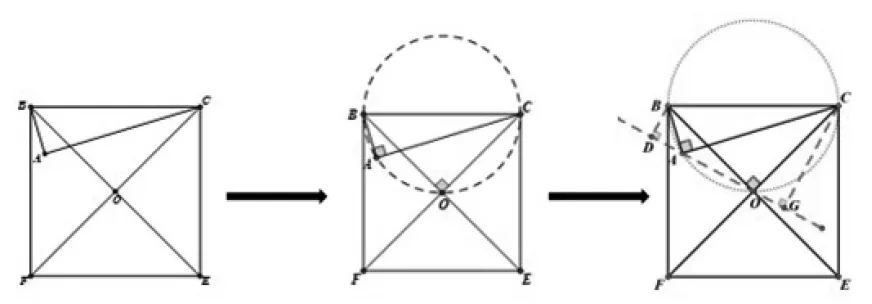
圖16

3.定角定弦的隱圓_建立應用圓周角定理構造圓的意識

如圖17，點D 是動點，點A、B 是定點，當滿足∠ADB=α（α 是一個固定值），那么點D 的運動軌跡是在以I 為圓心，IA為半徑的優弧AB 和以AB 為對稱軸的另一側的優弧AB，結合一個定點到動點D的距離，可求最大值與最小值問題。

圖17

幾何綜合題圖形構建復雜，問題解決需要綜合思考，教學中可引導學生靈活應用以上解決問題基本思考方法，學會從復雜圖形中還原命題原來的基本幾何圖形模型，培育學生會用數學的眼光觀察事物；促進學生在學習中形成常態化的思維習慣，培育學生會用數學的思維思考；合理表達如何從復雜圖形分解成基本幾何圖形，借助基本幾何圖形將復雜問題轉化的思維過程，培育學生用數學的語言表達，達到提升學生解決這類綜合問題的能力。［4］