例談新定義問題的特點與解題路徑

顧曉峰

[摘 ?要] 新定義問題的解決要求學生在新情境中利用已有知識直接或間接地解決問題，對學生思維的靈敏性、綜合性有著較高的要求. 文章通過對相關題目進行梳理和歸納，總結新定義問題的主要特點并提出解題路徑.

[關鍵詞] 新定義問題;特點;數學思維;解題路徑

研究背景

在近幾年全國各地的高考、模擬考試中，新定義問題因其設計新穎、思路開闊、追本溯源等特色而愈發受到命題者青睞，也開始有越來越多的一線教師進行研究. 不過，現有的研究成果并不多，且多局限于題型梳理，少有對該類問題的解決策略進行總結和提取[1][2][3][4]. 筆者通過對新定義問題的大量梳理并結合高三復習教學時學生解決該類問題的實際情況，總結新定義問題的特點、求解策略，形成一般研究路徑，以期給讀者提供一些素材與建議.

新定義問題特點

1.問題類型

從內容上看，新定義問題的類型可分為：新定義概念和新定義運算. 新定義概念是在已有數學概念的基礎上，重組或變化一些條件，生成新的名詞或通過給出新的性質來定義一個新概念;新定義運算是根據基本的運算法則和運算律，生成一種新的運算算理. 在一定程度上，新定義問題不完全是創新題，因為其依然根植于數學的基礎概念、基本方法與基本思想.

從新定義的融入方式來看，可以分為附加式、變異式和沉浸式. 附加式指問題的本質依然是明確使用已有知識進行處理的常規問題，只不過是對其解決過程附加了一種說法或者對其結果附加了一個名詞;變異式指對已有知識進行重組，或者對原有問題加以掩飾而“異化”為新問題;沉浸式是指定義的條件獨立性強，問題背景與原有知識體系有差異甚至“產生沖突”，需要拋開固有套路而沉浸于新情境來解決問題.

2.問題命制

新定義問題的命制方法呈現出兩種趨勢，第一，高等數學知識的適度下放.如向量的外積（叉乘）、狄利克雷函數、凸函數、高斯函數、卡特蘭數等，將這些新知識低深度地與學生現有知識相融合;第二，將已有概念內容或數學方法重新整合使之“面目全非”，通過有效轉化便可“回歸本源”.

3.問題特性

創新性：新定義問題的背景新穎獨特，題目中常出現“定義”“規定”“稱為”等詞匯，定義內容與教材中的知識內容存在一定差異，并且有時表述抽象，要求學生必須首先仔細讀題并明其新意，再進行解題.

綜合性：新定義問題背景創新，綜合聯絡不同知識點和知識塊，綜合運用各類數學思想方法，全面考查學生分析問題與解決問題的能力.包括明晰新概念的構成要素，挖掘與已有知識的關聯并將已有方法進行遷移，對新問題進行轉化等，指向學生數學核心素養的培養.

速用性：新定義問題的解決是指學生在規定時間內迅速學習并立即使用一個新的數學知識，這意味著學生需要在沒有老師指導下的短時間內“現學現賣”，對他們的思維靈敏性要求很高.

新定義問題解決策略分析

1.按部就班

（1）直接應用與表示

例1 （2020無錫期末）回文聯是我國對聯中的一種.用回文形式寫成的對聯，既可順讀，也可倒讀. 相傳，清代北京城里有一家飯館叫“天然居”，曾有一副有名的回文聯：“客上天然居，居然天上客;人過大佛寺，寺佛大過人.”在數學中也有一類順讀與倒讀都是同一個數的自然數，稱之為“回文數”.如44，585， 2662等. 那么，用數字1，2，3，4，5，6可以組成4位“回文數”的個數為（ ?）

分析：本題屬于新定義概念，變異式問題. 新數列與熟悉的等差數列和等比數列的定義不同，并使用了較為“數學化”的語言來表述，雖精練但抽象.基于條件信息中的關鍵詞（“m項為0”“m項為1”“任意”“0的個數不少于1的個數”），將待求“規范01數列”的特征具體化：一共有8項，其中4項是0，4項是1，從前往后數無論數到哪兒，數到的0的個數都大于或等于1的個數. 根據轉化后的條件，必有a=0，a=1，a到a的情況則通過列舉法呈現，直觀地進行計數.

新定義問題解題路徑研究

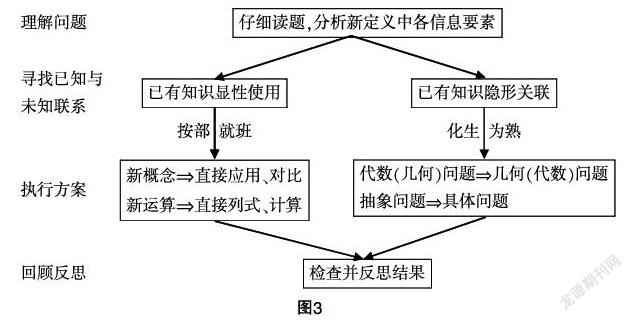
基于波利亞的經典解題范式[5]以及新定義問題的特點、解決策略的分析，下面提出該類問題的解題路徑（圖3）：

第一步：理解定義，熟悉問題. 通過認真讀題，確定題目的類型，理解定義中語言的表述，內容之間的邏輯關系以及目標是解決什么問題.

第二步：分析定義，制定策略. 分析新的定義與哪塊已學過的知識相關，是該部分知識的重組或是變式或是擴充？迅速建立起已知（已習得的概念、方法、思想）與未知（新情境、新條件、新目標）之間的關聯，制定解題策略.

第三步：利用定義，執行方案. 根據新定義的特點與解題目標，選擇數學工具，按照合適的策略進行處理. 在解題過程中，需要逐步檢查，來校驗每一步結果是否符合新概念或新運算所提出的要求（滿足定義的所有條件了嗎？轉化是否合理、等價？）.

第四步：回顧過程，反思定義. 解題完成后，回顧并審視關鍵步驟的嚴謹性，確保結果的可靠性，并進一步反思結果，加深對新定義的認識.

參考文獻：

[1] ?虞懿. 賞析2016年高考新定義型創新題[J]. 高中數學教與學，2016（12）：34-37.

[2] 姜世學. “新定義”型問題特征分析與解決策略淺析[J]. 上海中學數學，2018（11）：16-18.

[3] 黃杏，胡典順. 近年來高考數學中“新定義”題型解析[J]. 數學通訊，2018（12）：35-38.

[4] 楊國平. 新定義問題的三個常考題型[J]. 中學數學教學參考，2020（15）：77-78.

[5] 波利亞. 怎樣解題——數學思維的新方法[M]. 涂泓，馮承天譯. 上海：上海科技教育出版社，2012.