基于最優傳質系數的槽型結構參數對液膜機械密封汽化特性影響及優化

許曉東，馬晨波，孫見君，張玉言，於秋萍

（南京林業大學機械電子工程學院，江蘇 南京 210037）

引 言

液膜機械密封作為非接觸式機械密封的典型型式，可借助動壓效應增大液膜開啟力，形成端面間全流體潤滑狀態，有效降低端面磨損。在工業生產中端面液膜汽化現象越來越普遍[1]。目前易揮發或易汽化的液體介質在流體工業領域的應用越來越多，當泵在運行時，機械密封端面溫升將會導致端面間液膜發生汽化，使得端面流體膜處于汽液混相狀態[2-3]。

由于流體膜處于兩相狀態時，相較于全液膜密封其穩定性較差，所以液膜相變問題成為影響密封工作穩定性和可靠性，甚至導致密封失效的直接因素之一[4]。已有研究表明，雖然相變在一定條件下可以提高液膜承載能力、控制泄漏[5]、降低端面摩擦扭矩，但是超過一定條件之后則會導致不利影響[6-8]，如汽化會導致端面液膜完整性受到破壞，使得分離的動靜環端面出現接觸情況，造成密封端面磨損、汽蝕損傷、端面熱裂等密封失效。

目前，國內外不少專家學者對液膜機械密封相變問題展開了相關研究。Hughes 等[9]、Gu[10]發現可以通過監測端面溫度及壓力曲線進行相變界面位置的預測。顧永泉[11-12]根據相變界面位置將汽液兩相流分為似液相混相及似汽相混相密封，并提出以最大汽相體積分數及膜壓系數來進行結構合理性判斷。甘延標[13]、Safari 等[14]、呂知盛[15]基于格子玻爾茲曼方法提出不同類別的Thermal LB模型用于解決汽化相變問題。陳匯龍等[16-18]基于黏溫效應、飽和溫度隨壓力變化方程和流體內摩擦效應建立汽化相變計算模型，分析討論了螺旋槽液膜密封相變機理，研究了工況參數對液膜汽化特性及密封性能參數的影響規律。曹恒超等[19-21]、Wang 等[22-23]建立了螺旋槽等液膜相變模型，計算得到了密封間隙內流場與端面壓力分布，分析了工況參數及結構參數對液膜相變的影響，研究了相變區域對密封性能的影響。陳銀等[24]、馮瑞鵬[25]、張國淵等[26]利用仿真分析軟件，結合實驗分析，基于不同工況條件下密封性能變化提出結構參數優化設計。馬潤梅等[27]針對汽化對密封穩定性影響，設計了5 因素5 水平的正交優化實驗方案，為密封結構優化設計提供理論基礎。陳匯龍等[28]通過響應面法及均勻試驗法研究分析了端面型槽結構參數對開啟力、泄漏量的影響規律。

在采用計算流體動力學（CFD）方法模擬冷凝或沸騰過程時，存在Lee 模型[29]及Thermal LB 模型，因為Lee 模型具有形式簡單、易于計算、可靠性高等優點而被廣泛使用。然而，在相關研究中，Lee 模型中的傳質方程存在一個傳質系數，其中基于Fluent 軟件進行汽化仿真分析研究取默認系數[19-21,30]。邱國棟等[31]提出在CFD 模擬汽化相變時，傳質系數可以選取較大值，并且取值越大，計算精度越高。

為此，本文以螺旋槽上游泵送機械密封為幾何模型，建立基于黏溫方程、流體內摩擦、飽和溫度與壓力關系方程的液膜汽化計算模型，通過CFD 方法分析計算不同傳質系數對液膜相變的影響，研究在最優的傳質系數條件下槽型結構參數的變化對平均汽相體積分數的影響，并通過均勻試驗設計法和響應面法，分析結構參數之間的交互作用對平均汽相體積分數的影響，并對結構參數進行優化分析，為相變條件下螺旋槽機械密封的端面設計提供理論基礎。

1 模型建立

圖1為動環模型，Ro、Ri和Rg分別表示動環端面的外半徑、內半徑以及槽根圓半徑，θ1和θ2分別表示螺旋槽槽區及堰區對應圓心的角度，θ表示螺旋角，為螺旋線上任意一點的切線與其所在圓的切線的夾角。為了便于分析，做如下定義：槽徑比β=(Rg-Ri) /(Ro-Ri)，槽堰比γ=θ1/(θ1+θ1)。

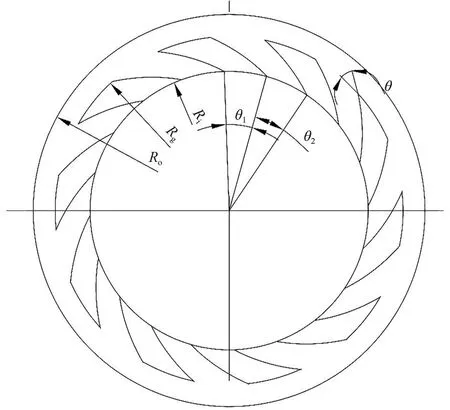
圖1 動環模型Fig.1 Dynamic ring model

螺旋槽液膜密封的相變機理非常復雜，為簡便計算，做如下簡化假設[32]：

（1）流體介質屬于牛頓流體；

（2）密封界面間的流體流動為連續介質層流流動，流體溫度和黏度不隨時間變化；

（3）密封面光滑，忽略其粗糙度對流體流動的影響；

（4）膜厚很薄，在厚度方向上壓力和密度保持不變；

（5）密封環的溫度及其材料的力學性能不隨時間變化；

（6）流體介質與密封端面之間無相對滑移；（7）忽略工作過程中系統的擾動及振動影響。

Lee[29]針對液相和汽相分別建立了獨立的守恒方程，其中傳質方程蒸發項和冷凝項分別如式(1)和式(2)所示：

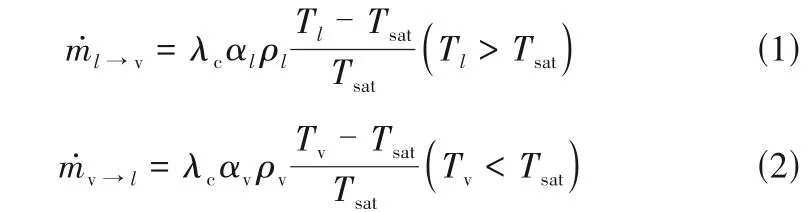
式中，Tsat為飽和溫度，K；λc為相變傳質系數，可通過實驗獲得；αl和αv分別表示液相與汽相的體積分數；ρl和ρv分別表示液相與汽相的密度，kg/m3。

ANSYS FLUENT 理論手冊[33]中給出了細泡狀流下界面濃度計算公式，可以計算得到每一個單元內汽相體積分數，其過程如式(3)：

式中，Ai為界面面積，m2；Vcell為單元格體積，m3。

沸騰及冷凝過程相變傳質系數λc可以用式(4)和式(5)來表達[33]：

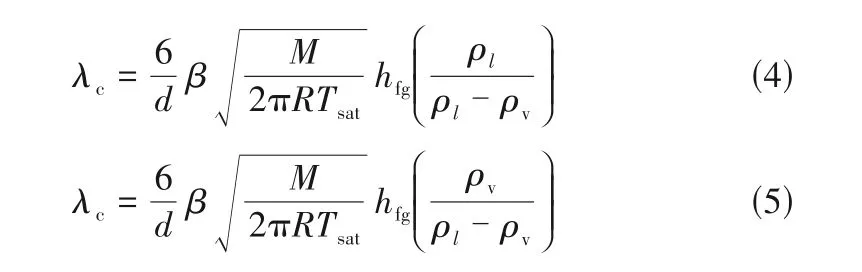
式中，d為汽泡直徑，m；β為調節系數；M為摩爾質量，kg/mol；R為通用氣體常數，8.314 kJ/（mol·K）；hfg為汽化潛熱，J/kg。

液膜出現相變之后，整個流體膜轉變為液體與汽體的均勻混合物，根據Wallis[34]對混合物的密度與黏度關系研究，式(6)可以準確解釋兩者間的聯系。

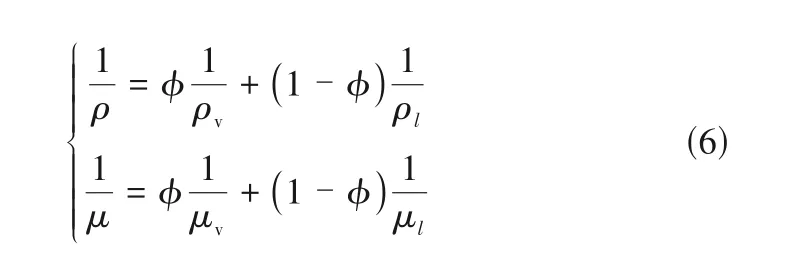
式中，μv和μl分別為汽相和液相動力黏度，Pa·s；φ為混合相中的汽相質量分數。

溫度不僅對液膜相變程度存在影響，還對液膜中液相的黏度及密封介質的飽和蒸汽壓力存在影響。汽相的黏度遠小于液相的黏度，并且受溫度的影響較小，基本可以忽略不計。本文中密封介質為液態水，汽相黏度取對應溫度下水蒸氣的黏度，而液態水的黏度與溫度之間的關系方程以及水的飽和蒸汽壓與溫度之間的關系方程由李新穩[35]的研究可得。

2 求解設置

2.1 計算域幾何模型

由圖1 可知，螺旋槽在動環端面上沿周向呈現周期性分布，可以認為各槽區及堰區的流場運動狀態相同。為了提高計算效率并降低計算成本，取其中一個槽區作為計算域，如圖2所示，其中圖2（b）為液膜厚度放大200 倍的計算流體域。通過Fluent 軟件中用戶自定義函數，將飽和溫度曲線方程及黏溫方程編譯并加載進Fluent軟件中。

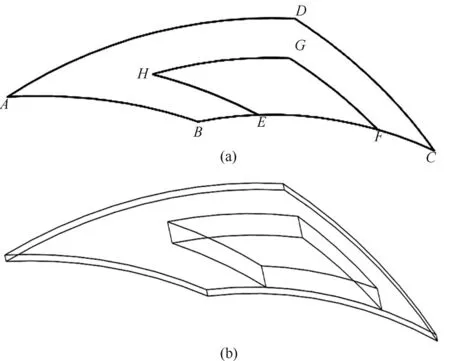
圖2 計算域幾何模型Fig.2 Computational domain geometry model

2.2 網格劃分

運用六面體結構網格劃分計算域。由于模型的槽深及膜厚為微米級，與模型其他尺寸參數相差數個量級，為達到計算精度要求，首先利用分塊功能將計算域分為螺旋槽區及液膜區，再通過對各區域邊界進行節點數定義以保證整體網格質量達到良好的計算精度[36]。

為了在滿足計算精度的同時降低計算成本，對網格數為79749、146397、257420、367819、577060 個時平均汽相體積分數進行了比較分析。在網格數為367819個時相對誤差為1.5%，平均汽相體積分數受網格的影響已經很小。同時考慮到網格數量對計算成本的影響，決定以該網格數量為標準進行網格劃分。

2.3 邊界條件及求解器設置

基于有限體積法對控制方程進行離散，選擇雙精度、壓力基求解器。多項流模型選擇Mixture 模型，相變模型選擇evaporation-condensation 模型，mass transfer coefficient 選擇0.1、2、4、6、48，算法選擇SIMPLEC 算法，壓力離散項選擇PRESTO！格式，動量及能量項選擇二階迎風格式，體積分數項選擇一階迎風格式，壓力松弛因子設為0.3，收斂精度設置為10-6。

計算域邊界條件設置如表1所示。

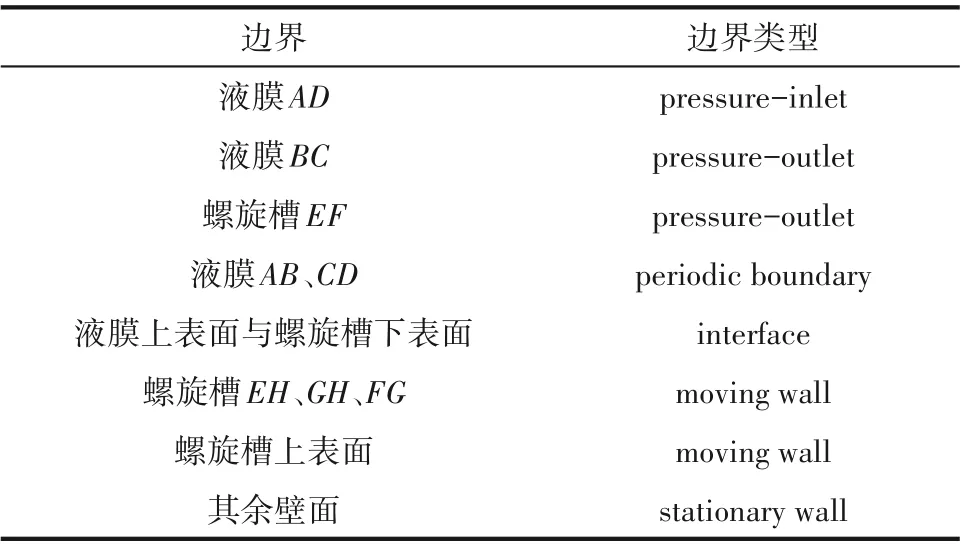
表1 邊界條件設置Table 1 Boundary condition setting

2.4 模型驗證與最優傳質系數確定

為了驗證模型的合理性，將仿真模擬計算結果與曹恒超等[20]（采用默認傳質系數0.1）所得結果進行對比，如圖3 所示。由圖3 中可以看出本文使用默認傳質系數（0.1）計算出的平均汽相體積分數數值與文獻中結果基本一致，驗證了仿真計算結果的正確性。但從圖中還可以看出，隨著傳質系數的提高，平均汽相體積分數逐漸增大且變化較為明顯。圖4 所示為平均汽相體積分數隨傳質系數變化曲線，從圖中可以看出，隨著傳質系數的增大，平均汽相體積分數急劇增大，但當到達一定數值后趨于穩定。當傳質系數設為48之后，每次計算得到的平均汽相體積分數相較于前一次計算結果，增長率已經低于1%，考慮到計算效率以及成本問題，本文選用48作為優化的傳質系數進行仿真計算。

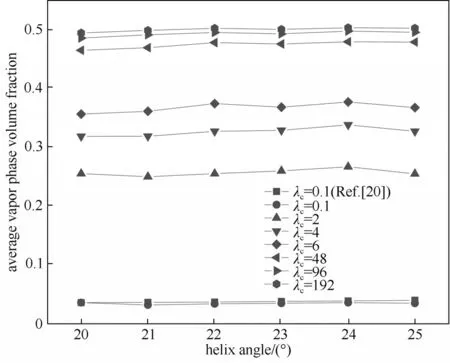
圖3 不同傳質系數條件下平均氣相體積分數隨螺旋角的變化Fig.3 Variation of average gas volume fraction with helix angle under different mass transfer coefficients

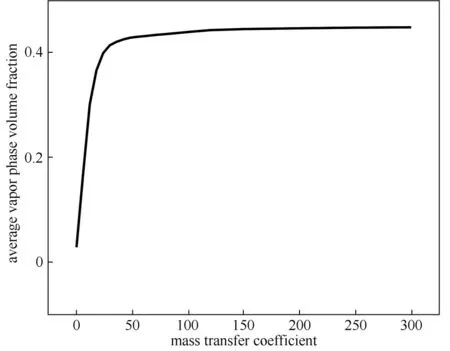
圖4 平均汽相體積分數隨傳質系數變化曲線Fig.4 The average vapor phase volume fraction varies with the mass transfer coefficient

3 結構參數影響分析

為了便于討論螺旋槽液膜密封型槽結構參數對平均汽相體積分數的影響，考慮到工況參數的改變會對以上密封性能參數造成影響，取壓力入口Pi= 1 MPa、入口溫度Ti= 393 K、出口壓力Po為標準大氣壓、出口溫度To= 300 K（環境溫度）、轉速n= 3000 r/min、槽數為12 個、端面外徑Ro=31 mm、端面內徑Ri=26 mm 作為固定參數。其余參數變化范圍如表2所示。

表2 槽型結構參數變化范圍Table 2 Variation range of trough structure parameters

3.1 均勻實驗設計

根據表2，系統設計4 因素、17 水平的均勻設計表U17(174)[37]，帶入設計變量參數后，根據每一組參數分別建立計算域幾何模型，運用CFD 方法進行數值模擬。相應的因素可以參數化設計為：

(1)螺旋角θ，記為x1；

(2)槽徑比β，記為x2；

(3)槽堰比γ，記為x3；

(4)槽深hg，記為x4。

由于上游泵送螺旋槽機械密封各結構參數之間存在交互影響，根據均勻實驗結果可以列出描述多個實驗因素（x1,x2, …,xm）與響應值（y）之間的二次多項式方程。本文所求的二次多項式回歸方程的格式為：

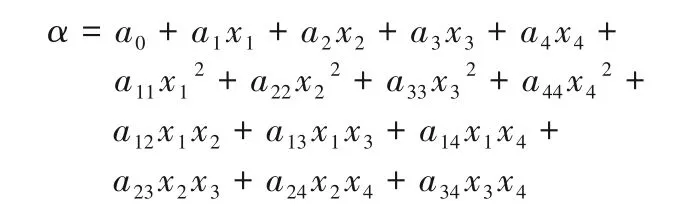
具體結構參數及計算結果如表3所示。

3.2 響應面法分析

將表3 中數據使用響應面法分析。圖5 所示為螺旋角、槽徑比、槽堰比、槽深兩兩相互作用響應面曲線及等高線圖。從圖中可以看出，在給定范圍內，槽徑比對平均汽相體積分數影響最大，其次分別為槽堰比、螺旋角，此外，螺旋槽槽深對平均汽相體積分數的影響最小。

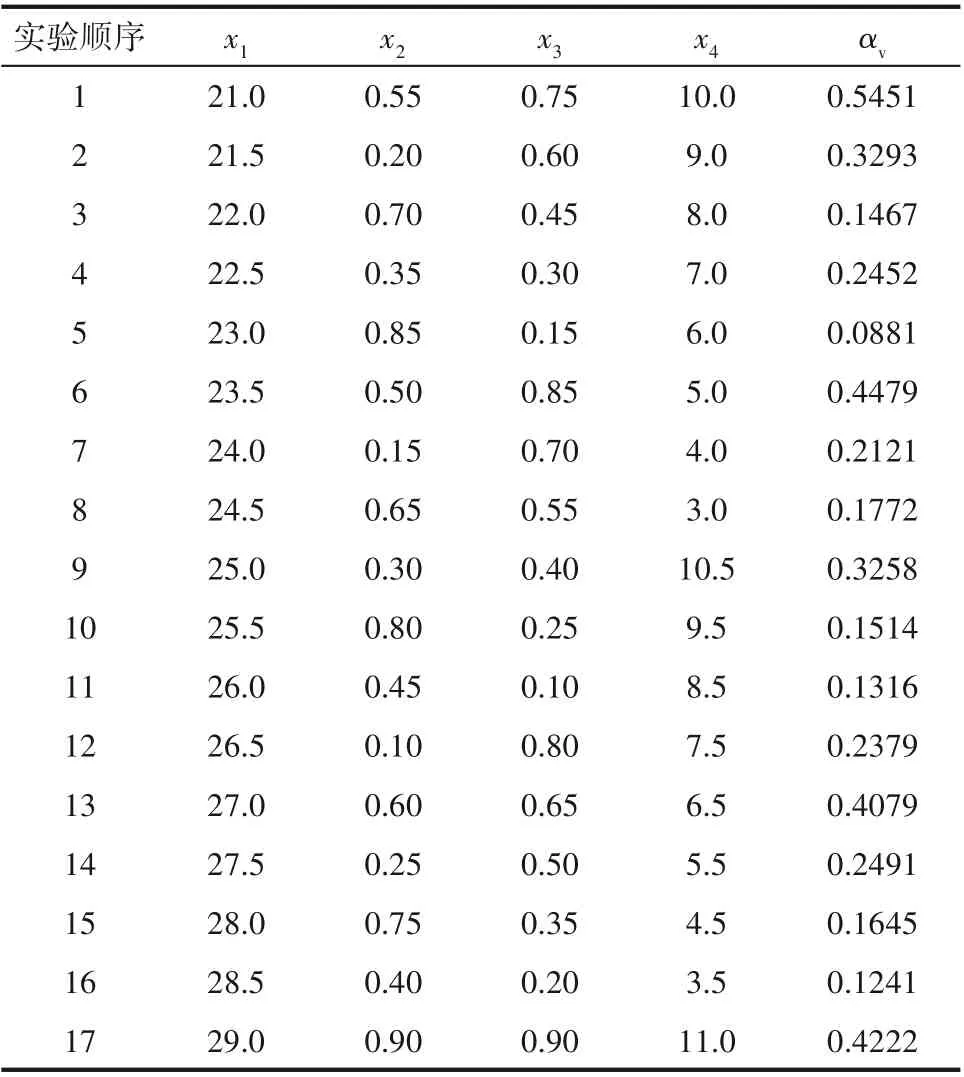
表3 均勻實驗表Table 3 Uniform experiment table

3.2.1 單因素分析 由圖5（a）～（c）可知，在螺旋槽θ處于20°到30°的范圍內，平均汽相體積分數隨著螺旋角θ的增大而不斷增大。螺旋角θ的增大，導致螺旋槽背風側工作面面積減小，同一時間內壓力突變增加，使得槽區范圍內壓力逐漸減小，且低壓區域逐漸增大，使得汽化相變區域不斷增大，從而導致平均汽相體積分數增大。

由圖5（a）、（d）、（e）可知，平均汽相體積分數隨著槽徑比的增加先增加后減小，在槽徑比為0.5 時取得最大值。當槽徑比較小時，螺旋槽背風側工作面面積較少，壓力突變區域較小，低壓區在整個液膜中不夠明顯，相變程度較低，平均汽相體積分數較低。隨著槽徑比逐漸增長，螺旋槽背風側工作面面積不斷增加，低壓區域范圍越來越大，相變程度不斷提高。然而，螺旋槽迎風側工作面的面積也在不斷增加，使得動壓效果越發明顯，在槽徑比為0.5時，螺旋槽區域的動壓效應對相變的抑制作用超過了低壓區相變的產生，從而有效抑制了相變的發生，導致平均汽相體積分數顯著降低。

由圖5（b）、（d）、（f）可以看出平均汽相體積分數隨著槽堰比的增加而增加。在槽堰比為0.1 時，兩個周期螺旋槽之間存在較大的堰區，槽區較小，液膜流動時形成的低壓區也較小，相變區域較小，造成平均汽相體積分數較小。隨著槽堰比的增加，堰區在兩個周期內所占的區域逐漸減小，而槽區逐漸增大，液膜低壓區域不斷增加，相變區域也不斷增加，平均汽相體積分數隨之增加。當槽堰比為0.9時，兩個周期螺旋槽之間的堰區最小，槽區最大，形成的低壓區域也達到最大，相變程度最高，平均汽相體積分數增大到最大。

圖5 交互作用響應曲面圖Fig.5 Interaction response surface plot

由圖5（c）、（e）、（f）可以發現，隨著槽深的增加，平均汽相體積分數不斷增加。隨著螺旋槽槽深的增加，螺旋槽背風側高度差不斷增加，使得液膜壓力突變程度不斷增加，低壓區域逐漸擴散，相變程度逐漸增加，造成平均汽相體積分數逐漸增加。

3.2.2 交互影響分析 綜合分析圖5（a）～（c），從圖5（a）中可以發現，槽徑比對平均汽相體積分數的影響在數值為0.5 處呈對稱分布的現象，并且隨著螺旋角的增大，其變化幅度越發顯著，并在槽徑比為0.45～0.55 之間存在平均汽相體積分數極大值；圖5（b）中體現了當螺旋角不變時，槽堰比的增加使得平均汽相體積分數增加，并且槽堰比越大，增長幅度越小。同樣，隨著螺旋角的增大，槽堰比的增大對平均汽相體積分數的影響逐漸減小；圖5（c）中可見螺旋角不變時，螺旋槽槽深的增加，使得平均汽相體積分數增加，當螺旋角增大時，螺旋槽槽深越深，平均汽相體積分數變化越顯著。

圖5（d）～（e）分別表示槽徑比與槽堰比和螺旋槽槽深之間的交互關系。從圖中可以看出槽徑比與槽堰比的交互影響遠比槽徑比與螺旋槽槽深的交互影響要顯著。圖5（d）中顯示的平均汽相體積分數分布規律與圖5（a）中顯示的結果一致，在槽徑比的變化范圍內呈對稱分布趨勢，并且都存在一個極大值。同樣，在槽徑比不變的條件下，槽堰比及螺旋槽槽深的增加，都會導致平均汽相體積分數增加。

圖5（f）表示的是槽堰比和螺旋槽槽深兩個因素對平均汽相體積分數的響應曲面關系，其交互影響顯著。可以發現，螺旋槽槽深一致時，平均汽相體積分數隨槽堰比的增大而增大，并隨著槽堰比的增加，螺旋槽槽深的增加導致平均汽相體積分數增長幅度越發顯著。

4 結構優化

非接觸式機械密封常見的失效形式有：端面磨損、汽蝕損傷、端面熱裂以及端面剝落等。引起這些失效的原因之一是液膜相變，當液膜發生汽化時，液膜的穩定性遭到破壞，兩端面出現接觸可能，以及汽化產生的氣泡的生成及潰滅會對端面造成沖擊，從而導致非接觸機械密封端面密封失效。所以螺旋槽機械密封在運行時，相變程度需要進行一定的限制，降低密封端面失效的可能性。

4.1 優化模型

本文研究發現，端面型槽結構參數的改變對平均汽相體積分數的影響較為顯著，所以為了控制汽化程度，滿足密封穩定運行要求，以平均汽相體積分數為優化目標，以螺旋槽的螺旋角、槽徑比、槽堰比以及螺旋槽槽深為變量進行優化設計。將表3中數據進行多元二次方程回歸分析，分析結果如表4所示。

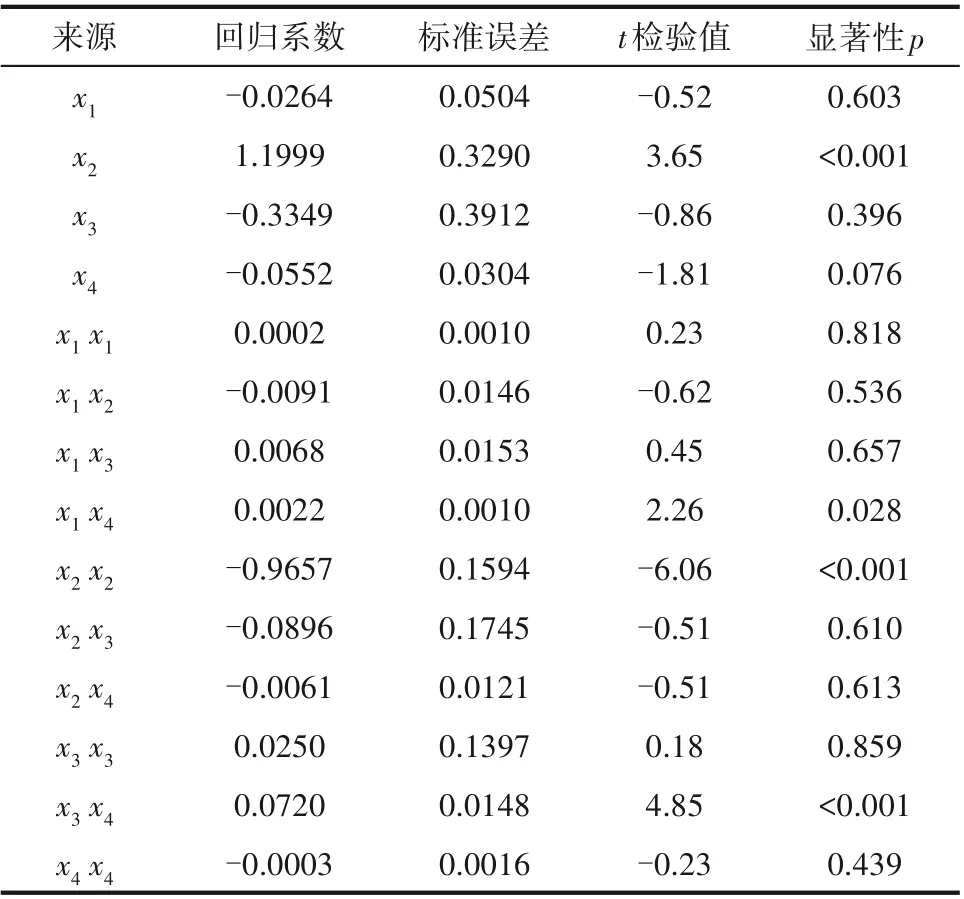
表4 系數顯著性分析Table 4 Coefficient significance analysis

通過對表3 中數據進行多元回歸分析，發現模型調整后的擬合優度R2接近1，且顯著性p＜0.0001，這說明該模型在實驗設計范圍內回歸顯著。雖然模型總體顯著性較好，但是不能說明所有因素項顯著性都很明顯，需要顯著性檢驗，結果如表4 所示。從表中可以看出，槽堰比與螺旋槽槽深之間的兩兩交互作用非常明顯（p＜0.001），螺旋角與槽深之間的兩兩交互作用顯著（p≤0.05），其余項的交互作用不顯著。

表3 中回歸系數為多元二次方程自變量系數，上游泵送螺旋槽機械密封平均汽相體積分數模型即為式(7)

4.2 遺傳算法及優化求解

利用仿真數據擬合得到的平均汽相體積分數與自變量型槽結構參數之間的多元二次方程關系式無法直接求解在變量范圍內的最優解，本文利用Matlab 遺傳算法工具箱進行輔助求解，遺傳算法相較于其余常規算法，更適用與求解較為復雜的組合優化問題。

遺傳算法具體流程如圖6所示。

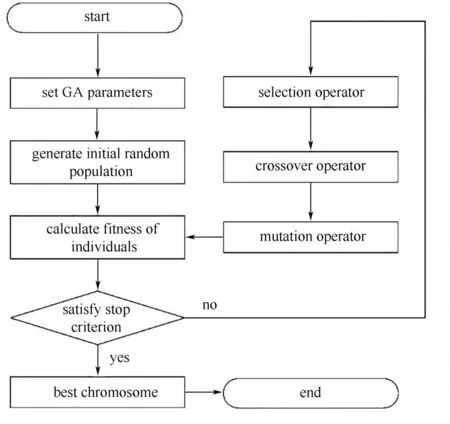
圖6 遺傳算法優化程序框圖[38]Fig.6 Program chart of genetic algorithm optimization[38]

（1）初始化設置：設置進化迭代數計數器t=0，最大迭代數為G，隨機生成N個個體作為初始值P(0)。

式(6)中包含4個自變量，根據常用和研究經驗，各自變量參數范圍分別為：x1選取螺旋角，取10°～30°；x2選取槽徑比，取0.1～0.9；x3選取槽堰比，取0.1～0.9；x4選取螺旋槽槽深，取3～15 μm。約束如矩陣A、b及式（8）所示。

（2）個體評價：計算群體P(t)中各個個體的適應度，本文選取式(7)作為個體的適應度函數。

（3）選擇運算：將選擇算子作用于群體。交叉運算：將交叉算子作用于群體。變異運算：將變異算子作用于群體。通過帶有猜測性質三種運算將群體P(t)推進到下一代群體P(t+1)。

（4）終止條件判斷：若t≤G，則t=t+1，并計算群體P(t+1)中各個個體的適應度。若t＞G，則終止計算，選取此前過程中計算得到最大適應度的個體作為最優解。

因為汽液兩相流機械密封在工作時，要保證密封穩定運行就需要對密封運行時的狀態進行限定，一旦平均汽相體積分數超過最大汽相體積分數，密封就處于似汽相混相密封，液膜會出現不穩定，最終造成密封失效，而處于似液相混相密封時密封性能良好。所以根據顧永泉[39]提出的液態水的最大膜壓系數對應的汽相體積分數范圍為10%～25%，這里為了確保密封不會因汽化出現失穩現象，選擇10%作為約束條件，如式(9)所示。

根據給出的優化約束條件，最終終止判斷條件變為，群體P(t)中個體的適應度滿足約束條件，并記錄其中具有最大適應度的個體。通過多次迭代計算，最終得到端面型槽組合優化結果，其中，螺旋角最優范圍為25.0°～28.0°；槽徑比最優范圍為0.10～0.30；槽堰比最優范圍為0.10～0.25；槽深最優范圍為4.0～6.0 μm。在本文給定工況范圍內，當槽型結構參數在上述范圍內選取，計算得到的平均汽相體積分數都小于最大膜壓系數對應的汽相體積分數，使得密封穩定運行。

5 結 論

本文計算分析了傳質系數對螺旋槽機械密封液膜相變的影響，并基于優化的傳質系數計算分析了端面型槽結構參數對端面間液膜密封性能影響規律及各結構參數間交互影響規律，得到以下結論。

（1）隨著傳質系數的增加，平均汽相體積分數先隨之增大后趨于平穩，傳質系數的影響不可忽略；

（2）顯著性分析結果表明，槽徑比對平均汽相體積分數影響極其顯著（p＜0.001），螺旋角、槽堰比及槽深對平均汽相體積分數影響較顯著（p≤0.05）；交互項中槽堰比和槽深交互影響極其顯著（p＜0.001），螺旋角和槽深交互影響較為顯著（p≤0.05），其余交互項的交互影響不顯著（p＞0.05）;

（3）平均汽相體積分數隨著螺旋角、槽堰比、槽深的增大而增大，隨著槽徑比的增大先增加再減小。槽深越深，平均汽相體積分數隨螺旋角及槽堰比的增大顯著增加;

（4）研究多因素共同作用及交互作用對平均汽相體積分數影響十分必要，相較于單一因素的影響更準確。通過遺傳算法分析得到螺旋角最優范圍為25.0°～28.0°；槽徑比最優范圍為0.10～0.30；槽堰比最優范圍為0.10～0.25；螺旋槽槽深最優范圍為4.0～6.0 μm。