高超聲速飛行器滑模控制參數整定方法設計*
程志浩,王 鵬,湯國建
(國防科技大學 空天科學學院空天工程系·長沙·100854)
0 引 言
高超聲速飛行器[1]一般是指飛行速度大于馬赫數5的飛行器,其大空域、寬速域的機動特性對控制器性能提出了很高的要求。滑模變結構控制具有魯棒性強、響應快、物理實現簡單的特點[2],被廣泛應用于飛行控制系統的設計中。在實際的飛行任務中,一套固定的控制參數往往無法滿足整個飛行過程的需求。通常情況下,控制參數需要人工根據經驗手動調試,過程十分繁瑣,調試得到的控制參數品質不高,也只針對于當前工況。因此,研究一種控制參數整定方法,使得飛行器能夠根據變化的氣動環境快速在線修正控制參數是十分有意義的。
近年來,遺傳算法、模擬退火算法、粒子群算法[3-7]等智能算法飛速發展,被廣泛用于解決控制參數整定問題。這類方法的整定效果尚可,但算力需求大,求解速度一般。強化學習是近年來的研究熱點,一些專家學者也將其應用于控制參數整定問題中。文獻[8]提出了一種基于Actor-Critic 結構的策略,以解決PID參數整定問題,但Actor網絡對應3個PID控制參數,各自的梯度不好給出,最后解得的3個控制參數存在耦合。文獻[9]沿用了文獻[8]中的方法,針對單個控制參數的滑模控制器進行參數整定,取得了比較好的效果。文獻[10]采用強化學習思想,實現了飛行器俯仰姿態PID控制參數的自主調度,但存在超調量過大的問題。文獻[11]引入連續動作學習自動機(Continuous Action Reinforcement Learning Automata,CARLA)算法,對自抗擾控制參數整定進行了一定的探索,但由于待求解量過多,懲罰函數設計不甚合理,導致算法收斂速度慢。總的來說,當前的控制參數整定方法研究已經取得了一些成果,但主要面向PID控制參數的整定,對其他控制方法的控制參數整定涉及較少,且整定速度一般,不能很好地滿足高超聲速飛行器控制參數整定的快速性。為了解決這一問題,本文改進了基于強化學習思想的CARLA算法[12],將其應用于高超聲速飛行器滑模姿態控制器的控制參數整定問題中,并與遺傳算法和模擬退火算法進行對比,以體現該方法的優勢。
1 飛行器運動模型與滑模控制器設計
本文采用文獻[13]中建立的高超聲速飛行器氣動模型為研究對象。為了簡化起見,忽略地球自轉,采用如下的縱向飛行器運動模型
(1)
式中,D為阻力;L為升力;g為重力加速度;m為飛行器質量;v為飛行器速度;h為飛行器高度;x為飛行距離;Re為地球半徑;ωz為飛行器俯仰角速度;Mz為控制力矩;Iz為飛行器Z軸轉動慣量;φ為俯仰角;α為攻角;θ為速度傾角。
(2)
其中
eφ=φ-φc
(3)

對滑模函數求導可得
(4)
俯仰角的二階導數可表示為
(5)
選用指數趨近律[14]作為趨近方式,這樣滑模函數的一階導數可以改寫成
(6)
其中,εφ、kφ為滑模控制參數,符號為正,可根據實際控制需要選取;sgn(·)為符號函數,將式(6)代入式(5)中,得到基于指數趨近律的滑模控制律為
(7)
當系統狀態點穿越滑模面時,由于式(7)中符號函數的存在,會導致控制量發生較大幅度的抖動,這一現象會嚴重影響控制系統的控制性能。為了盡可能地減少抖振帶來的影響,采用連續化的方法,以飽和函數sat(s)代替符號函數

(8)
滑模控制律變為
(9)

(10)
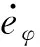
2 CARLA算法的改進
控制參數整定可以歸結為一種優化問題。學習自動機(Learning Automata,LA)是求解隨機優化問題的有效工具,它通過與環境的互動實現對概率分布的學習。CARLA算法是LA的一種,采用一種非參數化的概率模型,選取有限區間作為動作集,通過一個對稱的、高斯型的鄰近函數,將表現好的動作的獎賞傳播給其相鄰的動作[15]。由于CARLA算法本質上是一種基于概率的更新的算法,不可避免地存在一定方差,且多數情況下找到的為次優解并非最優解。但控制參數整定問題區別于一般的優化問題,有以下特點:1)控制參數不需要嚴格最優,滿足一定的指標能夠使控制器有較好的控制性能即可;2)控制參數的小范圍浮動對控制性能影響十分有限,對求解精度的要求可適當放寬;3)假設最優控制參數為a,那么實際選取的控制參數在靠近a的過程中,系統對應的控制性能也會提高。這3個特點使得該算法十分適用于控制參數整定問題。
引入CARLA算法的思想整定控制參數,總體思路為:將控制器和控制對象組成的系統當成環境,系統在不同控制參數下的控制性能反映了這組參數的品質,對于品質良好的控制參數,增大其出現的概率,反之減少。控制參數的概率分布在區間內不斷學習更新,最終會以高品質的控制參數為中心收斂,概率密度最大值對應的控制參數即為性能優越的控制參數。
文獻[11]采用CARLA算法解決自抗擾控制參數的整定問題,取得了一定效果,但也存在以下幾個問題:1)沒有對整定區間進行合理的離散化處理,導致抽樣占用的計算資源過大;2)待尋優的控制參數過多,導致僅有部分參數的概率收斂;3)回報函數設計存在不合理之處,導致收斂速度過慢。本文就這3個方面對CARLA算法進行了改進,并將其應用于滑模控制參數整定,算法的設計過程具體如下:
對于滑模控制器第i個控制參數xi,給定一個相應的學習區間Xi
Xi={xi|xi(min) (11) 式中,xi(min)為該控制參數的最小取值;xi(max)為該控制參數的最大取值。初始情況下,每個控制參數服從區間上的均勻分布 (12) 在進行控制參數選取時,每個參數通過其在區間內的概率分布進行抽樣選取。考慮到本文模型對控制量的精度需求并節約算力,在抽樣時需要對區間進行一定的離散化處理,具體的參數學習區間和離散程度設計如表1所示。 表1 控制參數的求解區間及離散點數目 (13) 式中,ai為第i個控制參數的離散點數目,式(13)相當于對概率指標進行了歸一化處理,每次選取控制參數時,各控制參數根據自己的概率密度分布進行抽樣。將選取的控制參數組合應用到控制系統中可得到性能指標。 定義控制性能評價指標如下 J(k)=c1Ess+c2ts (14) 式中,k為迭代次數;Ess為穩態誤差百分數;ts為調節時間(這里選擇10%準則);c1、c2為權重因子,根據控制性能的側重性進行設計。在飛行器的姿態控制回路中,受飛行器結構和控制機構執行能力的限制,飛行器角速度ω一般不超過30(°)/s,對本文的控制方法來說,ω受限時不會產生超調,因此J(k)中不含超調量項。若要將本文提出的算法應用于其他的控制參數整定問題中,則可按需添加該項。雖然這些指標各自的量綱不同,但只要該組合能夠充分反映系統的控制性能就可以作為系統學習的目標函數。 原始的CARLA算法中回報函數定義為 (15) 式中,J(min)為迭代過程中性能指標的最小值;J(avg)為平均值。式(15)的主要思想是,若本次迭代得到的性能指標小于以往的平均值,則給予獎勵。由于沒有懲罰的存在,獎勵給予的標準較低,導致算法求解效率不高,本文將回報函數改進為以下形式 (16) 得到每次迭代的回報后,每個控制參數的概率密度分布函數則進行相互獨立的更新 (17) 式中,H(xi,k)是以第k次迭代中選取的第i個控制參數值為中心的高斯分布,具體表達式為 H(xi,k)= (18) 式中,b1、b2為設計參數,影響控制參數學習的速度和分辨能力。g(k)是為了保證每個控制參數在其學習區間內的概率密度之和為1的歸一化因子,具體表達式為 (19) 將算法的總流程總結為圖1所示。 圖1 控制參數整定算法流程圖Fig.1 The flow chart of the control parameter setting algorithm 如圖1所示,每個控制參數的概率初始都服從學習區間上的均勻分布,隨著迭代的進行,各個控制參數的概率分布會以能提高系統控制性能的控制參數為中心增大,性能指標低的控制參數則會被不斷淘汰。迭代次數越多,找到最優解的可能性就越大。式(17)給出的更新公式既能使概率密度朝著高品質的控制參數方向進行更新,同時由于抽樣具有隨機性,算法也能在給定區間內進行充分探索,避免陷入局部最優的情況。算法的終止條件可設置為迭代達到一定次數或者性能指標滿足某個設定值。 選取飛行高度25km,以4000m/s的速度水平飛行的環境進行繞質心控制仿真,攻角α初始值為0°,并對攻角大小為5°的階躍指令進行響應,依照圖1的流程,取c1=2,c2=1,b1=0.01,b2=1.5運行算法,每次循環視為一次迭代,設定迭代次數100次后終止,仿真結果如圖2所示。 (a) dφ的概率分布隨迭代次數的變化 從圖2(a)~圖2(c)可以看出,隨著迭代次數的進行,3個控制參數的概率分布逐漸收斂到高性能的參數值附近;圖2(d)中,平均控制性能指標也逐漸減小,在迭代次數達到20次時下降開始放緩,經過約100次迭代后,算法基本收斂。在迭代進行到84次時,出現性能指標最小值J(84)=0.819,此時控制參數組合為dφ=0.1,kφ=8.57,λφ=11.26,將這組控制參數組合代入系統進行攻角的階躍響應測試,結果如圖3所示。 圖3 最優控制參數仿真結果Fig.3 The simulation results of the best control parameters 如圖3所示,飛行器大約在0.5s左右完成了對5°攻角階躍信號的指令響應,響應過程快速平穩,且具有極小的穩態誤差。改進后的CARLA算法整定出的控制參數具有優秀的控制性能。 采用式(14)定義的控制性能指標,尋優的目標為最小化控制性能指標J,控制參數的求解區間與表1相同,分別調用模擬退火算法(初始溫度100℃)和遺傳算法(種群大小50,交叉概率0.75)進行求解,結果如圖4和圖5所示。 圖4 模擬退火算法求解效果Fig.4 The effect of the simulated annealing algorithm 圖5 遺傳算法求解效果Fig.5 The effect of the genetic algorithm 將三種算法的求解效果進行對比,結果如表2所示。 表2 三種算法求解效果對比 如表2所示,三種算法在各自收斂時整定得到的控制參數值十分接近,其中改進的CARLA算法和遺傳算法整定得到的控制參數性能指標要略好于模擬退火算法,單從整定效果來看,三種方法差距很小,但改進后的CARLA算法所需迭代次數遠遠少于其余兩種算法,在求解速度上具有顯著優勢。高超聲速飛行器由于其快速機動的特性,一套固定的控制參數無法滿足其工作需求,需要針對不同飛行環境快速批量獲取控制參數,改進的CARLA算法則很好地滿足了這一需求。事實上,工業應用對控制參數精度的需求并不苛刻。該算法還可通過犧牲精度再度提升求解速度。以文中模型舉例,kφ在整定時是把[0,10]的范圍等距離散為100個點,控制參數求解精度為0.1。若將離散點減少為20個,求解精度變為0.5,那么算法的收斂速度將會顯著提升,整定出的控制參數對應的性能指標則損失很小。實際中可根據對精度和求解速度的具體需求選取離散點數目。 本文改進了CARLA算法,并將其應用于高超聲速飛行器滑模姿態控制器參數整定問題。仿真結果表明,該算法能夠在給定求解范圍的情況下,通過100次迭代整定出一組性能優良的控制參數,使飛行器快速穩定地跟蹤攻角階躍指令。與模擬退火算法和遺傳算法的對比結果表明,在整定得到的控制參數性能相差不多的情況下,本文提出的算法在求解速度上有極大優勢,契合高超聲速飛行器控制參數快速獲取的需求。此外,改進的CARLA算法還能通過減少離散點的方式再次提升求解速度。由于該算法不依賴于模型,理論上也適用于其他控制參數的整定問題,但待求解的控制參數不宜過多,一般在4個以內時,算法的求解能力會較強。總體來說,本文的工作對相關實際應用有一定參考價值。

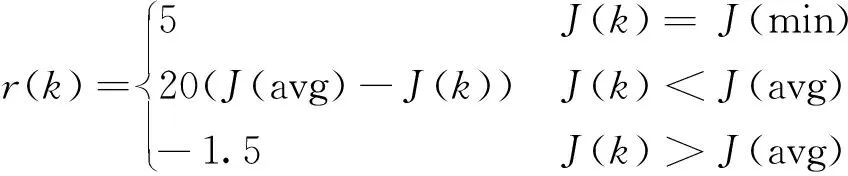
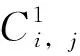
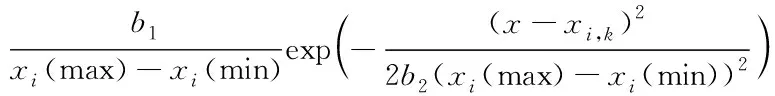

3 仿真校驗
3.1 改進的CARLA算法整定效果仿真


3.2 控制參數整定算法對比仿真



4 結 論

