HHT結合QPSO-GRNN的同塔雙回輸電線路故障測距

于仲安，陳 苗，張軍令

（江西理工大學 電氣工程與自動化學院，江西 贛州 341000）

0 引言

同塔雙回線技術在電力系統應用廣泛[1]。在同塔雙回線線路出現故障時，及時精準地計算出故障位置對于維持系統的穩定性、降低經濟損失十分重要。計算故障位置的方法現主要有2 類，即故障分析法與行波測距法。前者結合線路參數、故障參數、線路模型及序網圖進行大量的計算，進而得到故障位置：這種方法計算比較復雜[2-3]。行波法利用采集到的線路單端或者雙端故障初始行波波頭到達的時間數據，結合故障測距公式，經計算得到測距結果。相對于故障分析法，行波測距法計算量小，但是計算中存在波速不確定、雙端法波頭到達兩端時間不能嚴格同步等問題[4-5]。

人工智能的迅速發展使得模擬人腦工作原理的神經網絡成為研究熱點。在輸電線路測距過程中，通過神經網絡可以在對大量樣本訓練后找到輸入與輸出之間的關系并建立模型，進而實現預測出輸出值。目前，這方面的研究方向多集中在直流線路，交流線路僅針對單回線。文獻[6]將蟻群算法和Elman 神經網絡結合，用于直流線路測距；但是該方法存在輸入樣本固有主頻率難以提取的問題。文獻[7]發現，使用徑向基函數（radial basis function，RBF）在數據樣本比較少時測距精度不高。文獻[8]將從交流線路兩端采集的電壓信號進行S 變換，變換結果作為數據源輸入至測距函數，并采用粒子群優化（particle swarm optimization，PSO）算法進行測距；由于PSO 需要設置的參數過多，隨機性和不確定性強，導致粒子的速度不能得到很好的控制，易陷入局部最優解。

針對上述問題，在故障信號處理時，本文提出將希爾伯特黃變換[9]（hibert-huang transform，HHT）與智能算法中的量子粒子群（quantum particle swarm optimization，QPSO）優化廣義回歸神經網絡（generalized regression neural Network，GRNN）（后文簡稱QPSO-GRNN）相結合，對同塔雙回交流輸電線路進行故障測距：以電流特征模量希爾伯特黃變換所得采樣點為模型訓練過程中的輸入，對應故障距離為輸出，訓練得到最優光滑因子和測距模型。

1 QPSO-GRNN 模型

1.1 GRNN 模型

GRNN[10]是在RBF 的基礎上進行改進得到的，其特點是：具有很強的非線性映射能力；在樣本較少時仍能得到較好的預測效果；泛化能力強，網絡結構簡單，需要調節的參數少。

設x是自變量，y是因變量，其聯合概率密度為f(x,y)，x、y觀測值分別記為X，Y。Y的數學期望見式（1）：

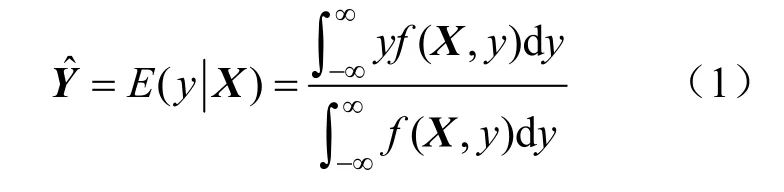
設輸入樣本x的維度為d，輸出維度為k，光滑因子為σ。當訓練樣本數為n時，經Parzen 非參數估計可得式（2）：

將式（4）代入式（3）中，可得式（5）：

GRNN 模型分為4 層，如圖1 所示。輸入層用于接收樣本，且輸入端口數與輸入樣本維數保持一致；在模式層將樣本處理完后，結果傳遞給求和層；在求和層，將各個樣本進行直接求和及加權求和；在輸出層，最終將加權求和結果與直接求和結果的比值輸出。

圖1 GRNN 模型結構Fig.1 GRNN model structure

對于GRNN，僅需調節適應函數的光滑因子σ的大小，就可改變模型輸出的效率及精確度；但光滑因子σ的選擇仍受人為因素的影響。當σ過小時，擬合能力較強，但泛化能力較弱，預測效果較差；當σ過大時，擬合能力、泛化能力和預測效果與σ過小時的結果相反。

為獲得最優的GRNN 模型，需尋找到最優的光滑因子σ。因此，通過引入量子粒子群優化算法對GRNN 模型中的最優光滑因子進行尋找。

1.2 基于QPSO 算法的GRNN 模型優化

標準粒子群算法中，粒子尋求最優解時易陷入局部最優。針對此缺陷，文獻[11]提出了一種模擬物理學中微觀粒子運動行為的量子粒子群優化算法。

與標準粒子群相比，量子粒子群全局極值搜索能力更強，需要設置的參數更少。由于粒子在微觀世界中不存在質量與慣性，因而其速度及位置值無法同時被精確觀測。由此，可利用波函數的統計屬性來估算粒子出現在空間某處的概率。用Schrodinger 方程計算概率密度，再使用Monte Carlo 隨機數法更新粒子位置。

假設d維空間中有m個粒子，表示第i個粒子迭代至t次，在第j(j=1,2,···,d)維的位置，則更新公式如下：

式中：u和?隨機分布在0～1 之間；α為QPSO 中的創新參數，一般取不大于1 的正實數。調節α便可改變粒子收斂速度；在QPSO 的粒子優化過程中，表示第i個粒子迭代更新至t次，第j維獲得的歷史個體最優σ，分別表示粒子群迭代更新至t次，第j維獲得的歷史整體最優σ以及個體最優σ的平均值；為吸引子，用于吸引粒子靠近。可根據式（7）（8）更新。QPSO 優化目標函數如式（9），所求為模型預測輸出值與實際值的最小均方差：

式中：emin表示最小均方差，需人為設置；y預測,i和y實際,i分別為模型訓練過程中預測輸出值和實際值。QPSO-GRNN 模型故障測距流程如圖2。

圖2 QPSO-GRNN 模型故障測距流程Fig.2 QPSO-GRNN model fault location process

1.3 輸入樣本的獲取

不對稱參數同塔雙回線的系統結構如圖3 所示。系統由兩端電源P、Q 供電，M、N 為同塔雙回線兩端。雙回線各阻抗符號見表1。

表1 線路阻抗符號含義Tab.1 Symbolic meaning of line impedance

圖3 同塔雙回線系統結構圖Fig.3 Structure of double circuit lines on the same tower system

同塔雙回線各相電壓、電流及阻抗的關系如式（10）：

式中：U、I表示線路電壓和電流；下標I、Ⅱ為線路標號；A、B、C 代表線路的三相。

相比于單回線，同塔雙回線方式節約輸電走廊，提高了輸電效率；但其相間和線間存在復雜的耦合，使得傳統的應用在單回線上的保護不能直接用在雙回線上，因此：首先需要對雙回線參數進行解耦。引用文獻[12]中的矩陣S對雙回線進行解耦。因雙回線參數不對稱，需引入不對稱參數K1、K2，得到總解耦矩陣M如式（11），解耦后得到電流模量I1—I6如式（12）所示。

式中：

根據式（12），模量1 和4 與I、Ⅱ回線均相關，模量2 和3 只與I 回線故障有關，模量5 和6只與Ⅱ回線故障有關，因此：模量2、3、5 和6可作為特征模量來判斷發生故障的線路。理想情況下，若只有線路I 故障，模量5 和6 數值應為0，模量2 和3 數值大于0；同理可得，當線路Ⅱ故障，若為跨線故障，4 個模量均大于0。

考慮到工程實踐中存在各種因素引起的不平衡電流，所以線路I 故障時，模量5 和6 數值并不為0；因此需設置一個門檻值ε1，保證在不平衡電流達到最大時也可不發生誤判。

定義2 個參數g1、g2：若g1=max{|I2|,|I3| }﹥ε1，則I 回線故障；若g2=max{|I5|,|I6|}﹥ε1，則Ⅱ回線故障。設置電流門檻值ε1= 0.2% × max{g1,g2}。根據ε1、g1、g2可判斷是否發生故障及故障時的線路。

確定故障線路后，選取對應的電流特征模量進行希爾伯特黃變換。希爾伯特黃變換由經驗模態分解（empirical mode decomposition，EMD）和希爾伯特變換（hilbert transform，HT）2 部分組成。希爾伯特變換要求信號必須滿足線性且穩態這2 個條件。工程實踐中所獲得的信號大多只能滿足這2 個條件其中一個，或無法滿足其中任一條件。EMD 的出現解決了這個問題：通過將輸入信號分解成多個固有模態函數（intrinsic mode function，IMF）分量，使其滿足希爾伯特變換要求；然后進行希爾伯特變換，即可得到故障初始行波到達兩端信號采集裝置的采樣點。以2 個采樣點作為QPSO-GRNN模型的輸入，故障距離為模型輸出，通過樣本對模型進行訓練，可得出采樣點與對應故障距離間的映射關系，實現模型故障測距。

2 仿真分析

在仿真軟件PSCAD 中搭建參數不對稱的同塔雙回線系統模型，如圖4 所示。

圖4 參數不對稱同塔雙回線系統模型Fig.4 System model of asymmetric parameters double circuit transmission lines on the same tower

部分參數設置界面如圖5 所示，圖中電壓等 級500 kV，頻率50 Hz，A 相發生接地故障。

圖5 仿真參數設置Fig.5 Simulation parameter setting

設置線路全長300 km，采樣頻率1 MHz，0.05 s處發生故障，故障持續0.02 s，仿真過程持續0.1 s。線路的具體參數見表2。

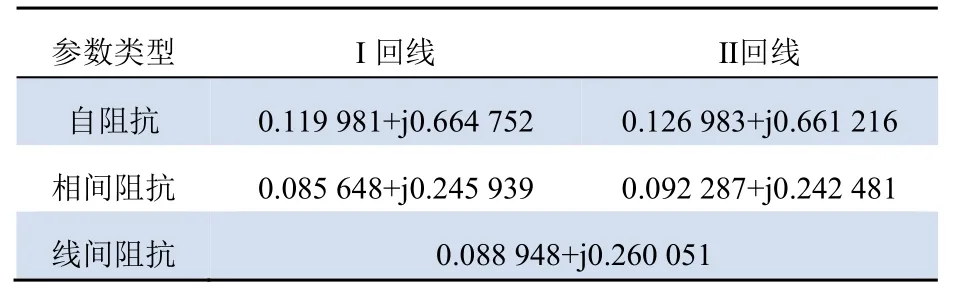
表2 線路參數Tab.2 Circuit parameters Ω/km

以第Ⅰ回線16 km 處A 相接地故障為例。采集線路兩端故障發生后0.02 s 的電流數據，并在MATLAB 中進行處理。圖6 為兩端模量I3經驗模態分解結果，圖中r表示無法再進行IMF 分量提取的剩余信號。圖7 所示為通過希爾伯特變換獲得的時間–頻率特性曲線。根據傳統的雙端行波測距公式可以估算出故障位置。公式如式（13）所示。

圖6 經驗模態分解結果Fig.6 Empirical modal decomposition results

圖7 時間–頻率特性曲線Fig.7 Time-frequency characteristic curves

式中：L為線路全長；v為波速，近似取光速；tM和tN分別表示故障行波波頭初始到達M、N 端的時刻；dM和dN分別表示故障處距離M、N 端的距離。

因采樣頻率設置為1 MHz，采樣點53 和948分別對應53 μs 和948 μs。根據式（13）計算得到的故障位置為15.75 km，測距誤差0.25 km。

因根據傳統行波雙端測距公式所得測距誤差太大，故提出：將其與智能算法相結合。點53 和948 可作為一組訓練樣本的輸入，16 km處數據為測距模型對應的輸出。在模型進行訓練時，以5 km 處為起點，每隔5 km 采樣一次，將過渡電阻分別設置為0 Ω，10 Ω，100 Ω；故障類型選取4 種，共590 組樣本，具體樣本見表3。以PSO 算法結合GRNN（后文簡稱PSO-GRNN）模型作為對比，任選其中 509 組樣本輸入到PSO-GRNN 和QPSO-GRNN 模型中進行訓練，剩余81 組進行測試。

表3 故障樣本數Tab.3 Number of failure samples

2.1 迭代次數對比分析

為更好地分析QPSO 和PSO 尋優過程中迭代次數的變化，在MATLAB 中對PSO-GRNN 和QPSO-GRNN 進行訓練。程序中設置迭代終止條件為最小均方誤差emin≤0.004 km 或迭代次數達到200 次。經過大量實驗，PSO 和QPSO 粒子數最終均設定為20；PSO 中慣性權重ω=0.6，加速因子c1=2，c2=2；QPSO 中α=0.6。2 種模型訓練迭代收斂曲線如圖8 所示。

根據圖8 可知，QPSO 迭代64 次后，達到由程序設置的均方誤差值，完成收斂；而PSO 則在迭代115 次后完成收斂。由此驗證了：QPSO 相比于PSO 收斂能力更強，速度更快。

圖8 2 種模型迭代收斂情況對比Fig.8 Comparison of Iteration convergence between two models

2.2 故障測距誤差對比分析

將81 組樣本代入模型進行檢驗。圖9 為測試樣本采用PSO-GRNN、QPSO-GRNN 及HHT 結合傳統雙端行波法（見公式（13），簡稱HHT）測距的誤差對比圖。

圖9 故障測距誤差對比結果1Fig.9 The first comparison fault location error

從圖9 可以看出：QPSO-GRNN、PSO-GRNN和HHT 這3 種方法最大測距誤差分別為0.074 km、0.1 km 和0.25 km。QPSO-GRNN 模型誤差最小；除個別測試樣本外，其整體測距效果優于PSO-GRNN。HHT 測距誤差最大。這證明了行波法與智能算法結合，可以克服雙端行波法采樣誤差、行波波速不確定等因素對測距結果帶來的影響；經QPSO優化的算法同時也克服了PSO容易陷入局部最優解的缺陷。相比990 組[13]和1 500 組[14]訓練樣本，GRNN 僅采用509 組就可達到較好的測距效果，從而驗證了其具有較強的泛化能力。

將模型推廣至參數對稱同塔雙回線情況。任意選取20組測試樣本代入已經訓練好的測距模型中，并與2 種行波測距法，即HHT 和小波變換[15]（wavelet transform，WT）做對比。其中WT 測距原理同HHT，利用兩端采樣點結合測距公式（13）可得到故障距離。3 種方法測距誤差如圖10 所示。據圖10 可知，QPSO-GRNN、WT、HHT最大測距誤差分別為0.069 km、0.15 km、0.21 km，且QPSO-GRNN 整體測距誤差小于HHT 和WT：這證明了所得模型測距效果優于2 種行波法，且針對參數不對稱同塔雙回線的測距模型對參數對稱同塔雙回線也具有較強的適用性。

圖10 故障測距誤差對比結果2Fig.10 The second comparison fault location error

用PSACD 仿真得到的樣本是建立在無噪聲干擾的理想情況下的。為了滿足工程實踐的要求，將40～50 dB 的高斯白噪聲加入訓練樣本中訓練，使QPSO-GRNN 模型具有一定的抗干擾能力；再將45 dB 的高斯白噪聲加入至測試樣本中。由圖11 可觀察到，模型測距誤差絕對值最大為0.083 km。這說明模型具有較好的抗干擾能力，能滿足一定的工程需求。

圖11 高斯白噪聲誤差圖Fig.11 Gaussian white noise error diagram

2.3 QPSO-GRNN 模型抗干擾能力分析

3 結論

本文提出HHT 結合QPSO-GRNN 的同塔雙回輸電線路故障測距方法。經仿真實驗，可以得出以下結論。

（1）使用本文模型，在參數不對稱同塔雙回線路故障距離預測過程中，無需對相關電氣量進行大量的演算與推導，僅通過相模變換和希爾伯特黃變換就可獲取輸入樣本，數據獲取方式簡單。

（2）QPSO 和PSO 相比，粒子搜索能力更強，收斂速度更快，能夠快速準確地找到最優光滑因子。使用QPSO 時，僅需設置一個參數，所以降低了多參數設置帶來的影響，測距精度更高。

（3）加入高斯白噪聲后，模型仍具有較高的故障測距精度，這說明模型具有較強的抗干擾能力。

神經網絡算法目前多應用于直流線路和單回交流線路故障測距；本文將QPSO-GRNN 用于同塔雙回線線路上進行測距，對后續進一步研究同塔多回線神經網絡智能測距方法有一定參考價值。