黏土中防沉板—樁復合基礎地震反應特性研究

關盛杰，孔德森, 2，王曉敏，鞏 越

(1. 山東科技大學 土木工程與建筑學院，山東 青島 266590；2. 山東科技大學 山東省土木工程防災減災重點實驗室，山東 青島 266590)

當前我國的海洋油氣資源開發正由淺海向深海發展[1]，深海的地質條件不同于淺海，在一些工程實踐中，作用在基礎上的荷載往往超過典型尺寸防沉板的承載極限，為了克服防沉板應用上的局限性，在防沉板下打入樁基礎組合成復合基礎，旨在不增加防沉板尺寸的前提下，依靠樁基礎將荷載傳遞到深層土體中，提高基礎的承載力，目前已經在石油開采項目中進行了工程實踐，隨后一些學者對其承載力進行了初步研究。

Dimmock等[2]假設僅防沉板承擔豎向荷載，防沉板和樁共同抵抗彎矩，提出了簡化的下限設計方法，然而這種簡化的方法只適用于在設計的可行性驗證階段初步估計復合基礎的承載力。Gaudin等[3]通過離心機試驗研究了混合基礎的承載性能，確定了混合基礎的破壞方式。這些研究多是針對工程設計實例的靜力學分析驗證[4-9]，作為水下生產系統的基礎，其上部承擔著生產設備等主要結構物，一旦發生地震，有可能造成破壞性后果，因此開展防沉板—樁復合基礎的動力學分析具有十分重要的意義。Zargar等[10]提出一種海上固定式平臺動力反應分析方法，在時域內考慮了土體非線性、樁土界面不連續、土體輻射阻尼引起的能量耗散、結構材料非線性和幾何非線性等因素的影響，并得出由于土體的非線性和輻射阻尼，使得平臺單元的位移更大，結構單元應力降低。Hesar[11]針對地震荷載下跳線、跨管連接等復雜集群產生的系統效應問題，介紹新的建模和模擬方法。段高松[12]研究了深海條件下輸入地震動特性和場地條件對防沉板動力反應的影響，并對比分析了基礎埋深、上部荷載及長寬比對基礎震陷的影響。

由此可見，防沉板—樁復合基礎進入工程應用以來，有關的地震荷載下動力反應分析的研究極少，為了給工程抗震設計提供有益參考和指導，采用Flac3D快速拉格朗日有限差分軟件分別建立典型防沉板尺寸與不同樁長組合的復合基礎模型，對比分析不同樁長下的復合基礎結構體系在地震荷載下的反應特性，對于完善防沉板—樁復合基礎的抗震設計理論和優化抗震結構形式具有重要意義。

1 計算模型建立

1.1 模型建立

以南海某深水防沉板工程為例，建立數值計算模型。參考已有的工程設計實例[13-14]，確定防沉板模型尺寸為10 m×5 m×0.2 m，角樁增設在防沉板四角，以“銷釘”方式連接來限制轉動。借鑒海上能源部門常用樁基尺寸參數，本次模擬的樁基直徑0.6 m，長度取4 m、6 m、8 m，三種樁長下的復合基礎編號分別為HSF-Ⅰ、HSF-Ⅱ、HSF-Ⅲ，并分別定義1～4號樁的順序，防沉板—樁結構體系如圖1所示。

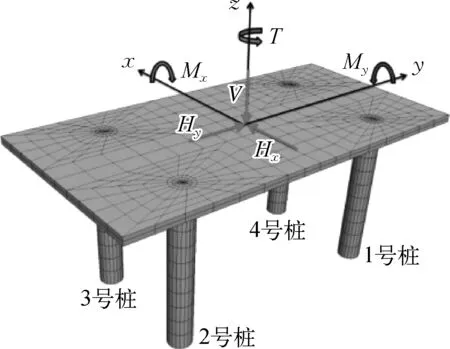
圖1 防沉板—樁結構體系平面圖Fig. 1 Plan of mudmat-pile structure system

復合基礎材料為理想彈性的高強鋼材，彈性模量E=206 GPa，泊松比ν=0.3，密度7 850 kg/m3。地震荷載作用下，復合基礎與土相互振動激發的應力波傳輸到邊界后會反射，從而影響計算精度，合理選擇模型尺寸可以減小邊界效應的影響。借鑒曹維科[15]的研究經驗，選取土體計算模型長50 m、寬25 m、深20 m。Flac3D的基本原理是通過求解運動方程來解決準靜力學和動力學問題，這兩類問題都涉及到阻尼問題，只不過對于靜力學問題需要設置更多的阻尼來使得模型快速達到收斂狀態，對于動力學問題，只要選擇合適的阻尼形式和阻尼參數即可描述土體和復合基礎在地震荷載下的動力特性，因此土體選擇Mohr-Coulomb本構模型。土體彈性模量E=48 MPa，泊松比ν=0.3，體積模量K=E/3(1-2ν)、剪切模量G=E/2(1+ν)，土體參數及作用在基礎上的設計荷載列于表1，設計荷載作用方向如圖1所示。

表1 土體參數及設計荷載

1.2 阻尼的確定

Flac3D提供了三種阻尼形式，其中，瑞麗阻尼動力計算時間步過小，計算負擔太重；軟件內置的滯后阻尼采用幾個連續的函數來表征模量的衰減，阻尼系數獲取困難；局部阻尼的原理是通過在震動過程中改變節點質量達到體系的快速收斂，當節點速度改變時即增加質量，當節點速度達到最大值或最小值時減小節點質量，整個過程中損失的能量ΔW與最大瞬時應變能W的比值與頻率無關而與臨界阻尼比D相關，因此可得如下方程：

αL=πD

(1)

式中：αL為局部阻尼系數，D為臨界阻尼比。

由此可見，局部阻尼系數獲取方便，不需要設置額外的參數。且對于Mohr-Coulomb材料而言，塑性流動可以耗散大量能量，選取額外的阻尼對于計算結果并不是那么至關重要[16]。因此本模型選擇局部阻尼，對于巖土類材料，臨界阻尼比D一般取2%～5%，參考前人的計算經驗[17]，臨界阻尼比取5%，局部阻尼為0.157 1。

1.3 邊界條件

數值計算模型動力邊界選擇自由場邊界，其原理如圖2所示，在模型的邊界處分別設置切向和法向阻尼器以吸收邊界處的反射波，模擬無限邊界模型效果，自由場模型包括四個側面以及四個角點處的自由場網格，側面網格與主體網格節點之間是一一對應關系，如圖3所示。主體網格的側向邊界通過阻尼器與自由場網格耦合在一起，從而實現了邊界條件的模擬，如果地面沒有結構物，主體網格和自由場網格一起移動，側向阻尼器將不會產生作用，當地面存在結構物時，側向阻尼器將發揮類似于安靜邊界的效果，吸收結構物震動產生的二次波。自由場網格的不平衡力施加到主體網格的邊界上，所施加的力按照下式進行計算：

(2)

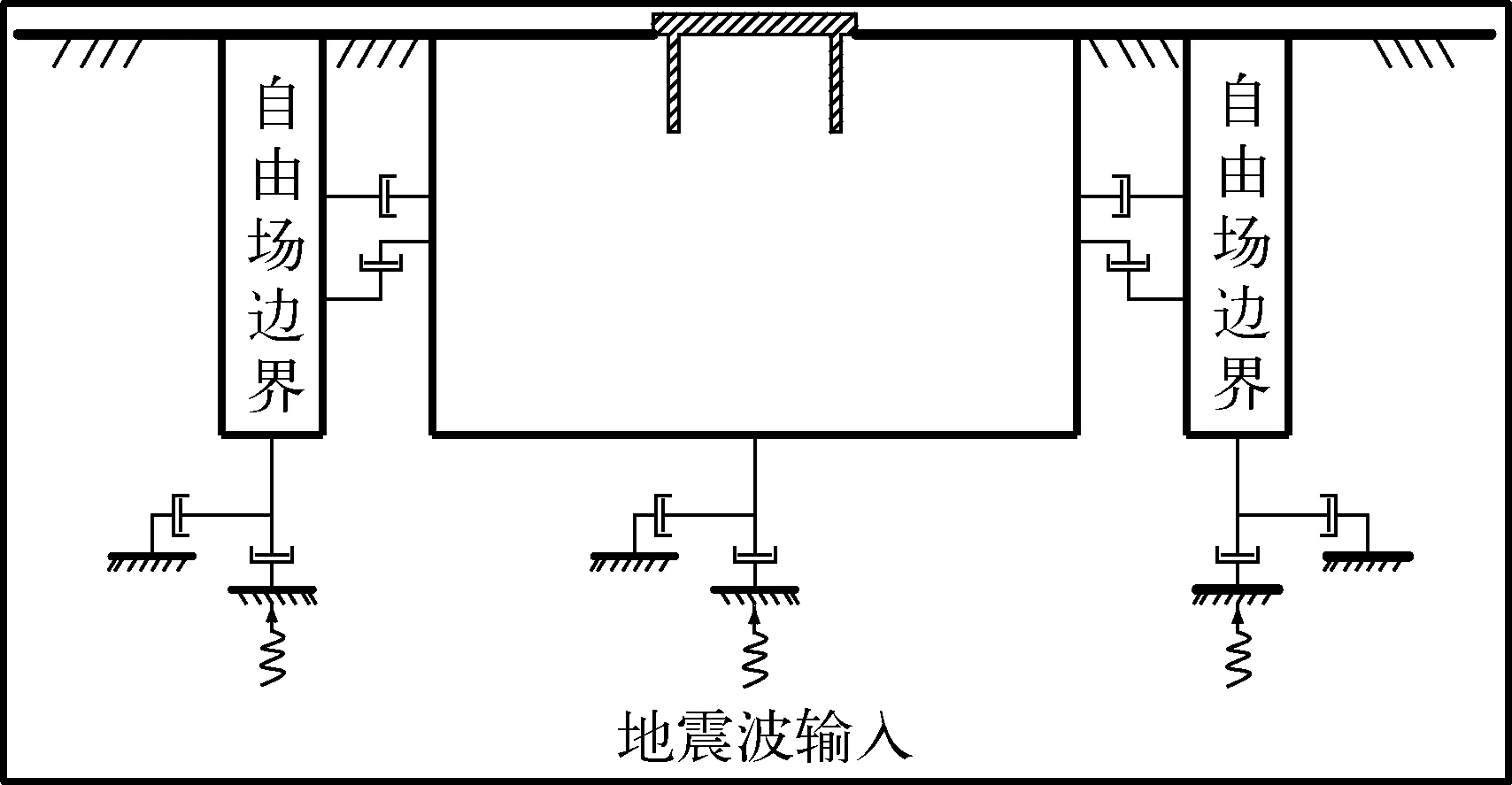
圖2 自由場網格與主體網格示意Fig. 2 Schematic diagram of free field grid and main grid

圖3 自由場邊界示意Fig. 3 Free field boundary diagram

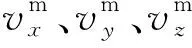
1.4 接觸面設置

采用“移來移去法” 建立接觸面，圖4為接觸面示意圖。Flac3D接觸面是由庫倫滑動、拉伸強度和剪切黏結來描述的，接觸面單元的本構模型如圖5所示，在每一個計算時步中，會計算出接觸面單元節點和所連接的目標表面的法向變形絕對值和相對剪切速度，根據接觸面本構模型，利用這兩個值可求出接觸面間法向力和剪切力矢量[18]。接觸面的法向彈簧剛度kn、剪切彈簧剛度ks、黏聚力c和摩擦角φ的取值參考文獻[17-18]，各參數列于表2。

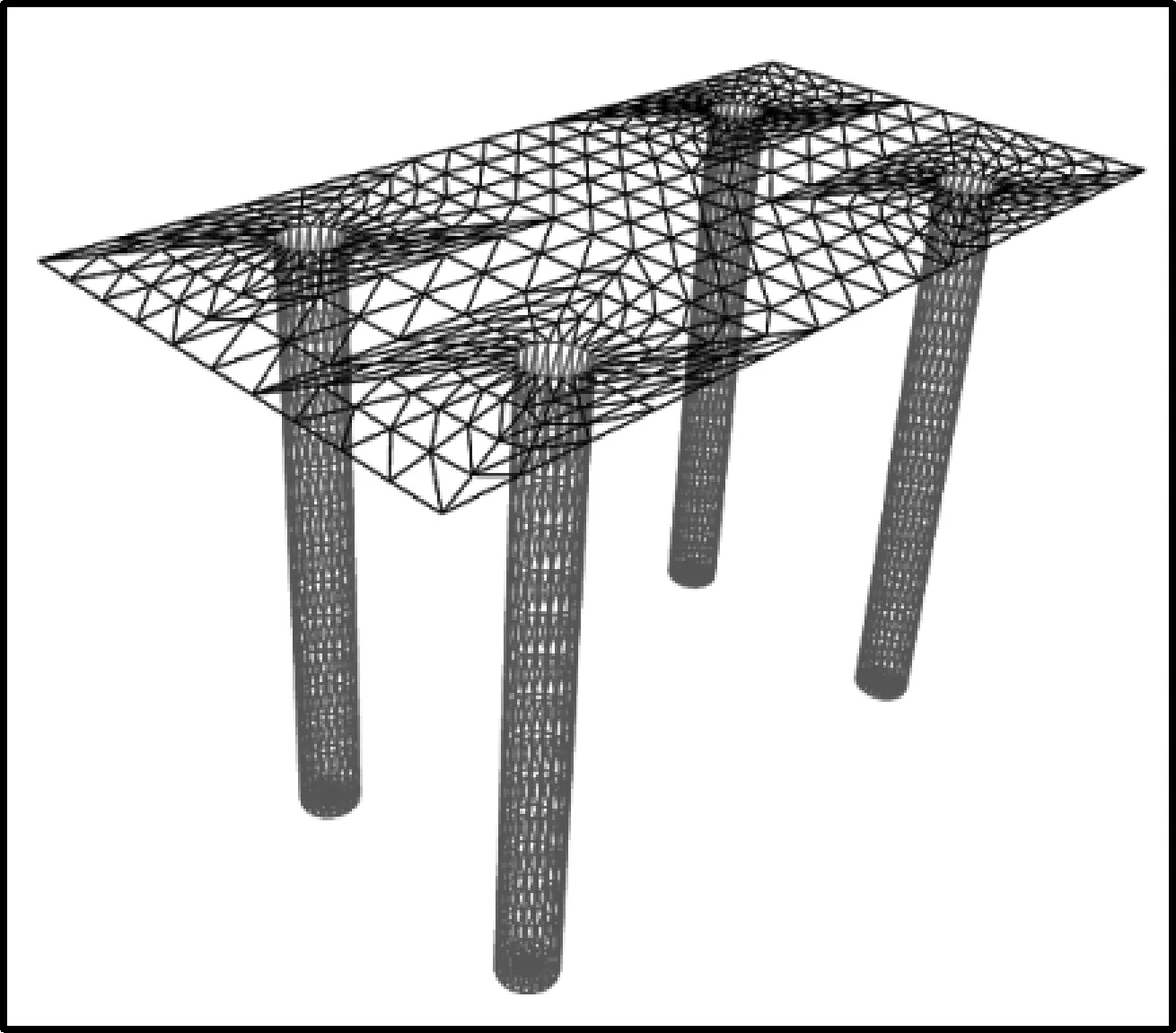
圖4 接觸面示意Fig. 4 Schematic diagram of the interface

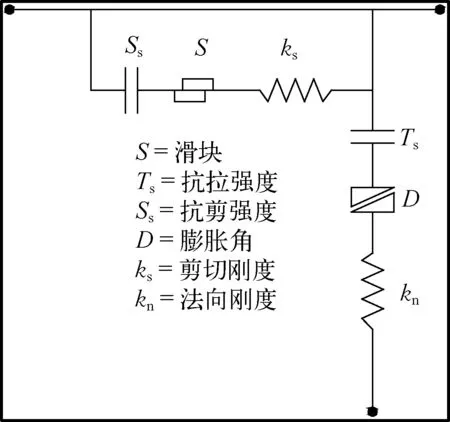
圖5 接觸面本構模型Fig. 5 Constitutive model of the interface

表2 防沉板和樁基礎接觸面參數

1.5 地震波的選取與輸入

選擇EL Centro地震波作為本次模擬的動荷載，加速度時程曲線如圖6所示，在0～2.14 s內加速度達到峰值0.35g，5 s之后加速度逐漸減小，較大的加速度主要集中在0～5 s范圍內，因此動力計算至5 s結束。地震波中的高頻波段對模型網格的最小尺寸有重要影響，過小的網格會直接限制了計算效率，因此采用Flac3D內置的Dynamic Input Wizard功能模塊過濾掉地震波的高頻部分，同時對計算結果又不會造成顯著影響。濾波完成后，對速度時程曲線和位移時程曲線進行基線平衡，避免動力計算結束時模型內部仍有殘余的速度與位移。土體模型底部為基巖，彈性模量E=1.28 GPa，泊松比ν=0.29，屬于剛性基礎，可不設置安靜邊界條件，直接將加速度施加在模型底面[19]，計算深度為20 m。

圖6 EL Centro地震波加速度時程曲線Fig. 6 Time-history curve of EL Centro wave acceleration

1.6 算例驗證

為了驗證自由場邊界和地震波輸入方式的合理性，選取50 m×25 m×20 m土體模型進行計算，模型底部為1 m厚的巖石，上部為土體，土體、基巖力學參數同前。采用線彈性本構模型，四周為自由場邊界，在底部施加剪切脈沖波：

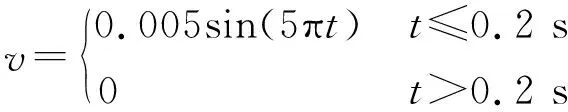
(3)

式中：v為施加的脈沖波速度，t為動力時間。

剪切波在土體中的傳播速度按照下式計算，脈沖波由底部傳輸到頂部所需的時間為0.185 8 s。

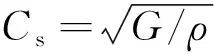
式中：Cs為剪切波波速，其余參數意義同前。

算例計算時間為1 s，分別監測模型底部、頂部的速度，其速度時程曲線如圖7所示，脈沖波從模型底部向上傳播，在0.1 s時底部速度達到峰值0.05 m/s，約經過0.181 3 s傳播到模型頂部，在0.293 2 s處頂部速度達到峰值，頂部因是自由界面脈沖波向下反射，從而速度峰值放大了2倍。在0.2 s之后，底部速度為零，頂部約在0.7 s出現第二個峰值，其原因為脈沖波傳播到基巖與土體分界面時發生反射，反射的脈沖波向上傳播再次到達頂部。由此可見，設置自由場邊界并以速度的方式施加地震波是合理的，具有較高精度。

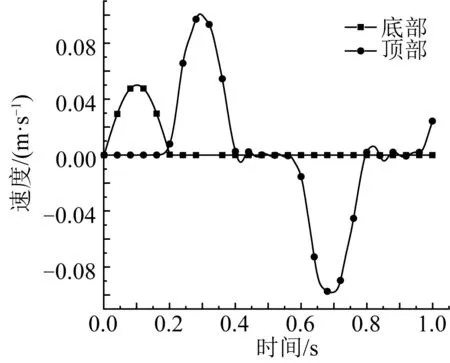
圖7 模型底部、頂部的速度時程曲線 Fig. 7 The velocity time history curve at the bottom and top of the model

2 動力反應特性對比分析

2.1 復合基礎加速度時程曲線對比分析

圖8是三種復合基礎位于防沉板中心點處的加速度時程曲線，對比發現，三種復合基礎的加速度時程曲線變化規律基本一致，加速度峰值約為輸入地震波加速度峰值的4倍，且峰值加速度均為瞬時加速度，說明地震波在向上傳播的過程中被放大；瞬時加速度存在的原因為土體底部存在模量較大的巖石[19]。

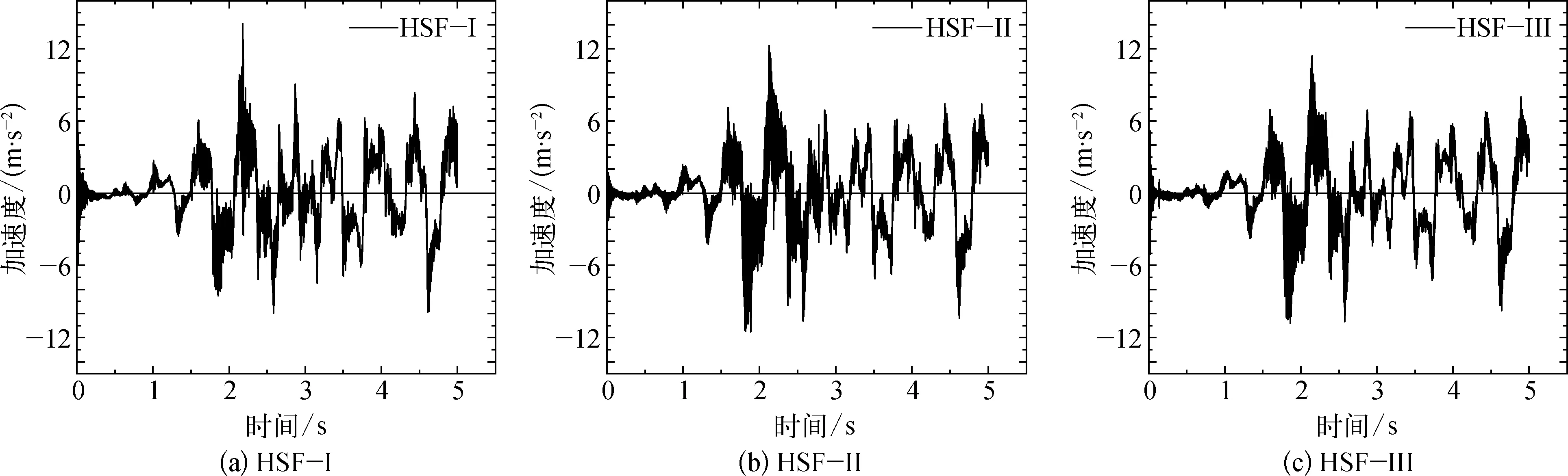
圖8 不同樁長下復合基礎的加速度時程曲線Fig. 8 Acceleration time-history curve of composite foundation under different pile lengths

與模型底部輸入的地震波相比，三種復合基礎頂部加速度達到峰值時間有一定延遲，輸入地震波在2.14 s處達到峰值，而樁長為4 m、6 m、8 m的復合基礎頂部到達峰值加速度的時間分別為2.18 s、2.15 s、2.14 s，樁基礎越長，復合基礎頂部到達峰值加速的延遲越小，其原因是在土層參數和震源能量相同的情況下，刺入土層的樁越長，震動能量越早的傳播到復合基礎結構體系中。在黏土場地上，土層對高頻地震波具有過濾作用[17, 19]，而防沉板幾何中心點處的加速度時程曲線高頻部分多于輸入地震波，原因為多個樁基礎之間的震動響應相互影響所致。三種復合基礎頂部的加速度放大系數分別為4.129、3.585、3.332，隨著樁長的增加，防沉板頂部加速度放大系數呈現減小趨勢，但減小的幅度隨著樁長增加而降低，說明在地震荷載作用下，增加樁長可以一定程度提高復合基礎的抗震性能；針對南海該特定工程，簡單的增加樁長對于提高復合基礎抗震性能意義不大，應當將樁長控制在6 m以內比較合理。

2.2 復合基礎位移時程曲線對比分析

圖9是三種復合基礎在防沉板幾何中心點處的x向絕對位移曲線，三種復合基礎的位移響應趨勢基本一致，其絕對位移值大小順序在不同時域呈現不同規律。仔細對比發現，由于土體的滯后性，復合基礎的位移響應幾乎總是滯后于輸入地震波位移。HSF-Ⅰ、HSF-Ⅲ兩者的x位移響應一致性較高，在水平移動方向轉變處幾乎總是產生更多的附加位移，其原因為：復合基礎受到三維組合荷載作用，在地震荷載作用下，當樁長為4 m時，樁基礎的嵌固作用較弱，復合基礎發生了旋轉產生了附加的x位移，該現象可從圖11復合基礎z向位移時程曲線得到驗證，HSF-Ⅰ的z位移上下波動，說明復合基礎發生了旋轉；當樁長為8 m時，樁長的增加不僅使得震動能量快速傳播到復合基礎(圖8所示)，而且HSF-Ⅲ高度增加且樁土模量差較大，HSF-Ⅲ基礎搖振劇烈。

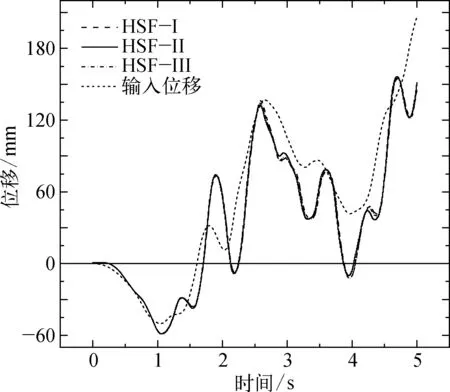
圖9 復合基礎x向絕對位移時程曲線Fig. 9 x displacement time history curve of composite foundation

為了量化三種復合基礎的位移響應，以HSF-Ⅰ的位移為基準，分別將HSF-Ⅱ、HSF-Ⅲ的位移與之作差，如圖10所示，Ⅰ-Ⅱ、Ⅰ-Ⅲ分別表示樁長為6 m、8 m時與樁長為4 m時復合基礎的x向相對位移差，在0～1.68 s，相對位移差在1 mm以內，在1.68 s之后，隨著地震波加速度的增大，相對位移差逐漸增大。對比分析發現，與Ⅰ-Ⅲ曲線相比，Ⅰ-Ⅱ曲線的震動波幅較大，與樁長6 m的復合基礎相比，當樁長為8 m時，復合基礎在x方向的位移響應值減小約3～4 mm，說明復合基礎在x向的位移響應值對樁長敏感，存在最優的樁長可使得復合基礎水平搖擺程度最低。

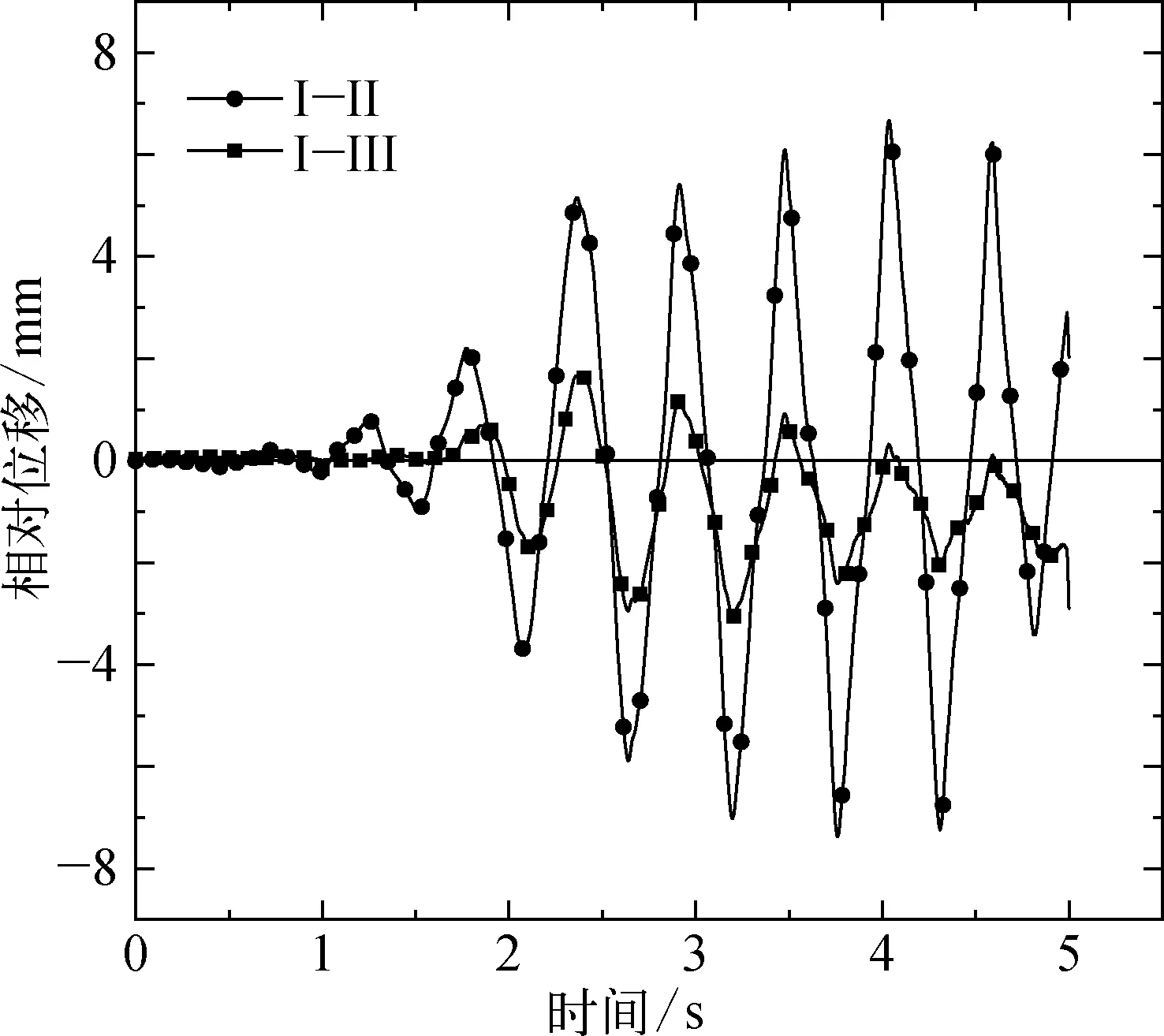
圖10 復合基礎x向相對位移時程曲線Fig. 10 x displacement time history curve of composite foundation

圖11是三種復合基礎在防沉板幾何中心點處的z方向位移時程曲線，對比分析發現三種復合基礎在z方向的位移響應規律基本相同，復合基礎在地震荷載作用下產生不可恢復的附加沉降，即震陷[12]。在0～1.6 s，由于地震波加速度較小，土體的地震響應較小，復合基礎的z向位移增加緩慢，在1.6～2.14 s，隨著地震波加速度增大，復合基礎的z向位移響應值快速增加，在2.14 s地震波加速度達到峰值，樁長為6 m、8 m的復合基礎的附加沉降約達到11 mm，而樁長為4 m的復合基礎豎向位移有較大波動。地震波峰值過后，三種復合基礎的z向位移仍有所增加，但增長幅度不大，說明基礎震陷在地震波加速度達到峰值時已基本完成，峰值過后不規則荷載所引起的附加沉降只占很小的部分。對比研究發現，HSF-Ⅱ的震陷量同比最小，z向絕對位移與樁長不具單調關系，其原因為：HSF-Ⅰ由于樁長較小而震動劇烈，對下部土體擾動影響較大，從而產生較多沉降；HSF-Ⅲ除了上述搖振現象劇烈外，還由于其樁基較長，樁基礎分擔了更多的外加荷載，當持力層受到持續擾動時，樁基下沉產生更多的豎向位移。

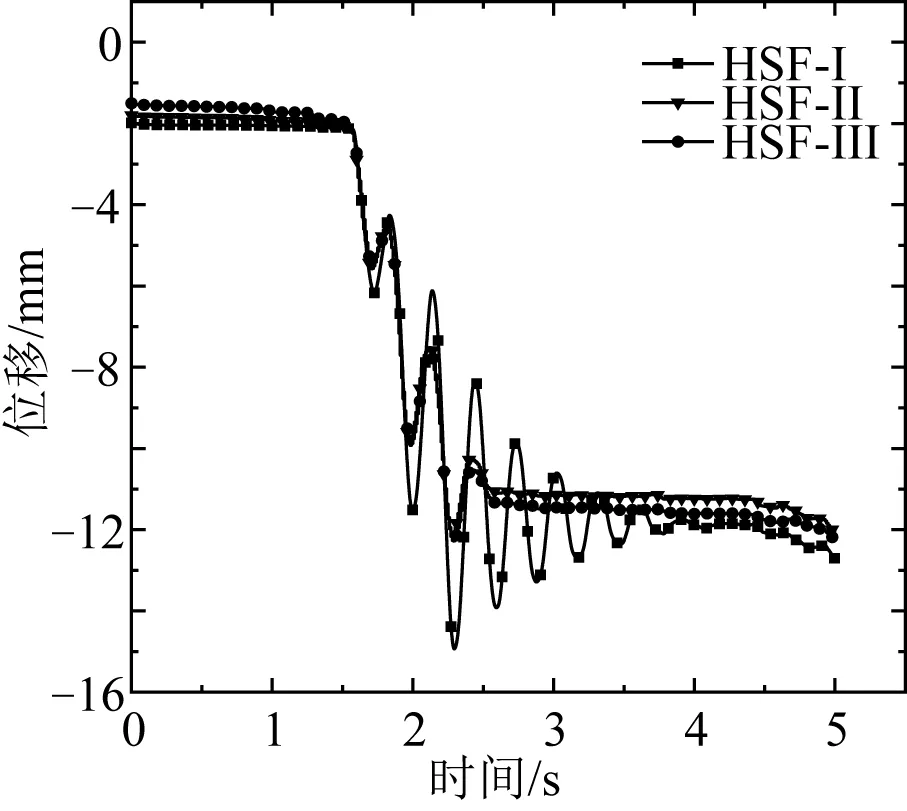
圖11 復合基礎z向位移時程曲線Fig. 11 Time-history curve of z-direction displacement of composite foundation

2.3 土體動力反應特性分析

為了研究地震荷載作用下復合基礎—土體系相互作用規律，分析土體的加速度數值響應差異，分別在近場、遠場及不同埋深處設置監測點，監測點方位如圖12所示。三種復合基礎不同埋深處內場、近場及遠場土體的加速度時程曲線如圖13所示，加速的峰值列于表3。

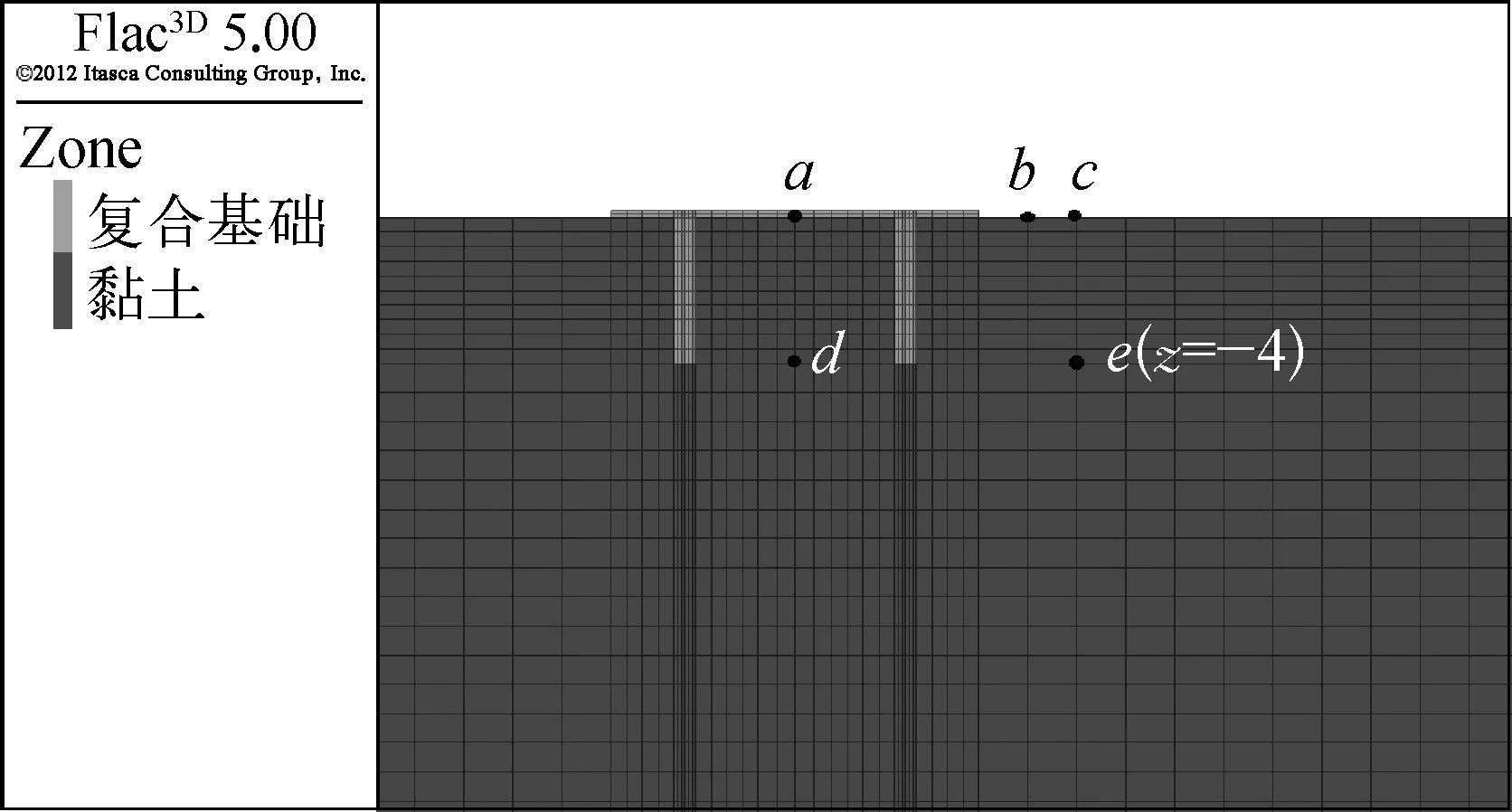
圖12 監測點布置Fig. 12 The arrangement of monitoring location

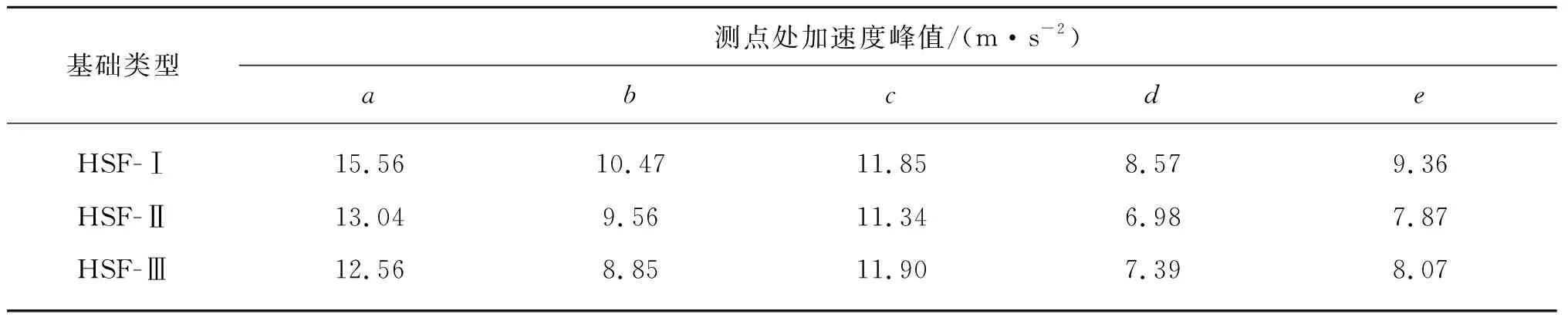
表3 不同位置處土體加速度峰值

圖13(a)、(b)、(c)分別為內場、近場及遠場地表土體加速度時程曲線，對比圖13(d)、(e)埋深4 m處的加速度時程曲線發現，地表處的加速度峰值均大于輸入地震波和埋深4 m處土體的加速度峰值，說明地震波在傳輸過程中被不斷放大，這與上述結論一致；受防沉板震動的影響，三種復合基礎內場地表土體加速度峰值分別為15.56 m/s2、13.04 m/s2和12.56 m/s2，明顯大于近場及遠場地表土體；并且防沉板、土體模量相差較大，內場地表土體加速度峰值大于防沉板幾何中心處。不同樁長下，遠場地表處土體的加速度峰值均大于近場土體，其原因是樁基礎的嵌固作用把防沉板頂部震動能量傳輸到了深層土體，從而距離復合基礎較近的近場土體的震動受到抑制，遠場土體因為距離較遠，能量傳播不受限，所以加速度峰值較大。在埋深4 m處，不同樁長復合基礎內場土體的加速度峰值分別為8.57 m/s2、6.98 m/s2、7.39 m/s2，對于遠場土體處這一數值分別為9.36 m/s2、7.87 m/s2、8.07 m/s2，遠場土體的加速度峰值均大于內場土體；并且當樁長為6 m時，復合基礎的內場和遠場土體加速度峰值均最小，原因考慮為HSF-Ⅱ的對周圍土體擾動較小，再次驗證上述結論。

2.4 樁身內力對比分析

動力時域內各樁樁頂與防沉板連接處的彎矩變化如圖14所示，對比分析發現，不同樁長下樁—板連接處的彎矩變化規律基本一致。在靜荷載作用下，位于荷載作用方向前端的1號樁、4號樁樁頂彎矩均大于2號、3號樁；由于樁長增加，荷載作用力臂變長，HSF-Ⅱ和HSF-Ⅲ的樁頂彎矩均大于HSF-Ⅰ。在地震荷載作用下，三種復合基礎的樁頂彎矩最大處均為1號樁與防沉板連接處，選取荷載時程為2 s時結果進行分析，三種樁長下復合基礎的樁頂彎矩分別為249 kN·m、427 kN·m、525 kN·m，相較于HSF-Ⅰ，HSF-Ⅱ、HSF-Ⅲ的1號樁樁頂彎矩增加了71.48%、110.84%，因此對于長樁復合基礎，應該在樁—防沉板連接處增設加固裝置。

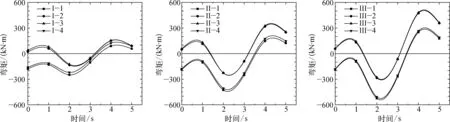
圖14 動力時域內樁頂彎矩Fig. 14 Bending moment of pile top in dynamic time domain

3 結 語

基于Flac3D有限差分軟件，建立了防沉板—樁復合基礎模型，土體選擇Mohr-Coulomb本構模型，模型底部輸入EL Centro地震波，分析了南海某工程中不同樁長的復合基礎在動力時域的地震反應特性，結論如下：

1) 隨著樁長的增加，防沉板頂部加速度放大系數呈現減小趨勢，減小的幅度隨著樁長增加而降低，在該工程背景下，應當將樁長控制在6 m內比較經濟合理。

2) 地震荷載作用下，復合基礎在x方向的位移響應值對樁長敏感，當樁長為6 m時復合基礎水平振動程度最弱；隨著地震波加速的增加，復合基礎會產生震陷，加速度峰值過后，沉降基本穩定，z向絕對位移與樁長不具單調關系，樁長為6 m時震陷量同比最小。

3) 由于樁基礎的嵌固作用，距離復合基礎較近的土體加速度響應值小于遠場土體。當樁長為6 m時，復合基礎對周圍土體擾動最小。

4) 地震荷載作用下，樁基礎與防沉板連接處彎矩值會增大，此處容易產生破壞。

當土體為飽和狀態時，在地震荷載作用下，土體內會產生超孔隙水壓力，從而對土體的強度和剛度、防沉板—樁復合基礎與土的接觸剛度等產生較大影響，因此，后續可考慮飽和黏土的孔隙水壓力變化規律，開展防沉板—樁復合基礎與土相互作用的流固耦合分析，以研究飽和黏土超孔隙水壓力的變化對防沉板—樁復合基礎地震反應特性的影響，從而為該區域工程建設提供理論參考。