砂土阻尼比確定方法對比分析

馮震， 郭濤， 宋東松

(1.河北大學建筑工程學院， 保定 071002； 2.河北省土木工程監測與評估技術創新中心， 保定 071002)

阻尼比主要反映土體動剪應力-動剪應變關系的滯后性特性，是土的基本動力特性參數，也是場地地震反應分析不可缺少的基礎性資料。阻尼比自20世紀70年代Seed等[1]對無黏性土的研究時出現以來，已經有50多年的發展歷史了，期間對砂土的研究較為充分，Amr等[2]對埃及鈣質砂的動力特性進行了評價；Jafarian等[3]對各向同性及異性條件下的鈣質-硅質砂的動力特性做了研究；Pradeep等[4]對印度北部砂土地震反應特性進行了研究；朱成浩等[5]對粉砂動本構模型做了研究；韓麗君等[6]對應力和應變控制下飽和砂土的循環扭剪特性做了研究。同時研究的土類也從無黏性土擴展到粉土[7]、黏性土[8]、海洋土[9]、凍土[10]、人工合成土等[11]。目前，中外對阻尼比的動力特性研究已經相對成熟，然而對阻尼比的確定方法卻沒有達成共識。

阻尼比確定方法大致可以分為兩類：滯回圈法和滯后角法(時間相位差法)。其中，滯回圈法在中外應用最為廣泛，阻尼比定義為一個周期內消耗應變能(滯回曲線的面積)與一個周期內儲存的應變能的比值，目前對儲存應變能的確定還不統一，陳偉等[12]、Das等[13]、李瑞山等[14]、Kokusho[15]、Kumar等[16]各自提出了不同的修正方法。滯后角法是一種傳統方法，根據剪應力-剪應變時程曲線來確定阻尼比[17-18]。具體是根據剪應力、剪應變間的時間相位差來確定，該方法對試驗數據的采樣頻率有較高的要求，數據點越多阻尼比的計算精度越高。

中外學者提出了多種確定方法來確定阻尼比，但是對于各種確定方法以及確定的結果之間的差異性尚不得知。因此，研究各種確定方法之間的差異性，以及確定合理的處理方法具有重要的研究價值。

為此，現以福建標準砂(粒徑0.5～1.0 mm)為試驗對象，采用動三軸試驗，選用傳統法、Das法、Kokusho法、Kumar法、互相關函數法為確定阻尼比的典型代表，將幾種方法確定的結果進行對比，評價它們之間的差異性，給出使用建議，為工程應用中合理選用阻尼比確定方法提供重要參考。

1 阻尼比確定方法

目前中外學者大多基于滯回圈法確定阻尼比，具有代表性的阻尼比確定方法及特點如下。

(1)陳偉等[12]對傳統使用等效橢圓計算一個周期內消耗的應變能進行了改進，提出了一種用多邊形逼近滯回曲線計算滯回圈的面積(一個周期內消耗的應變能)，該方法可直接利用試驗數據進行計算，算法可重復利用，使得阻尼比的計算工作得以簡化，目前中外學者大多采用此法來計算滯回圈的面積。

(2)Das等[13]、李瑞山等[14]指出傳統方法計算阻尼比時，在計算最大彈性應變能時只利用了正向加卸載半周的信息，對于理想對稱的滯回圈，這種做法較為理想，但在剪應變較大時，正向半周和反向半周出現不對稱情況，這種做法將會導致阻尼比結果偏差較大。對此，他們對傳統的方法進行了修正，取滯回曲線頂點連線與剪應變坐標軸圍成的兩個三角形面積(第一象限、第三象限)的均值為一個周期內儲存的應變能。

(3)Kokusho等[15]對傳統的方法進行了改進，考慮了剪應力、剪應變在大應變下滯回曲線正負半軸的不對稱性，對一個循環周期內存儲的應變能進行了修正，取滯回曲線頂點的連線，分別作縱橫坐標軸的垂線并交于一點，取圍成三角形面積的1/4為一個周期內存儲的應變能。

(4)Kumar等[16]對Kokusho法進行了改進，將滯回曲線頂點的連線修正為分別于原點連線，取圍成的多邊形的面積的1/4為一個周期內儲存的應變能。

同時，也有少數學者基于信號處理方法給出了阻尼比的確定方法，例如，羅飛等[17]根據凍黏土的剪應力-剪應變滯回曲線特性，提出了確定凍黏土阻

尼比的互相關函數法；梁珂等[18]對相關函數法進行了拓展，根據相關函數反映兩個波形在不同時刻的相似程度的物理意義，采用互相關函數分析應變滯后于應力時程波形的相位差，進而計算阻尼比。

為充分認識各種阻尼比確定方法之間的差異，以及確定結果之間的差異性，現選用以下幾種確定方法為典型代表。

1.1 傳統法

美國土工試驗標準D3999[19]對阻尼比的定義為

(1)

式(1)中：λ為阻尼比；WD為一個循環周期內消耗的應變能；WS為一個循環周期內存儲的應變能。如圖1所示，滯回圈的面積表示WD，陰影部分的面積表示WS。

對于一個循環周期內消耗的應變能WD的計算，陳偉等[12]提出了一種可使用原始試驗數據多邊形逼近剪應力-剪應變滯回曲線的方法，直接進行滯回圈面積的計算，一個循環周期內消耗的應變能計算公式為

(2)

式(2)中：τi為一個循環周期內記錄的剪應力；γi為一個循環周期內記錄的剪應變；n為一個循環周期內記錄的剪應力-剪應變點總數。

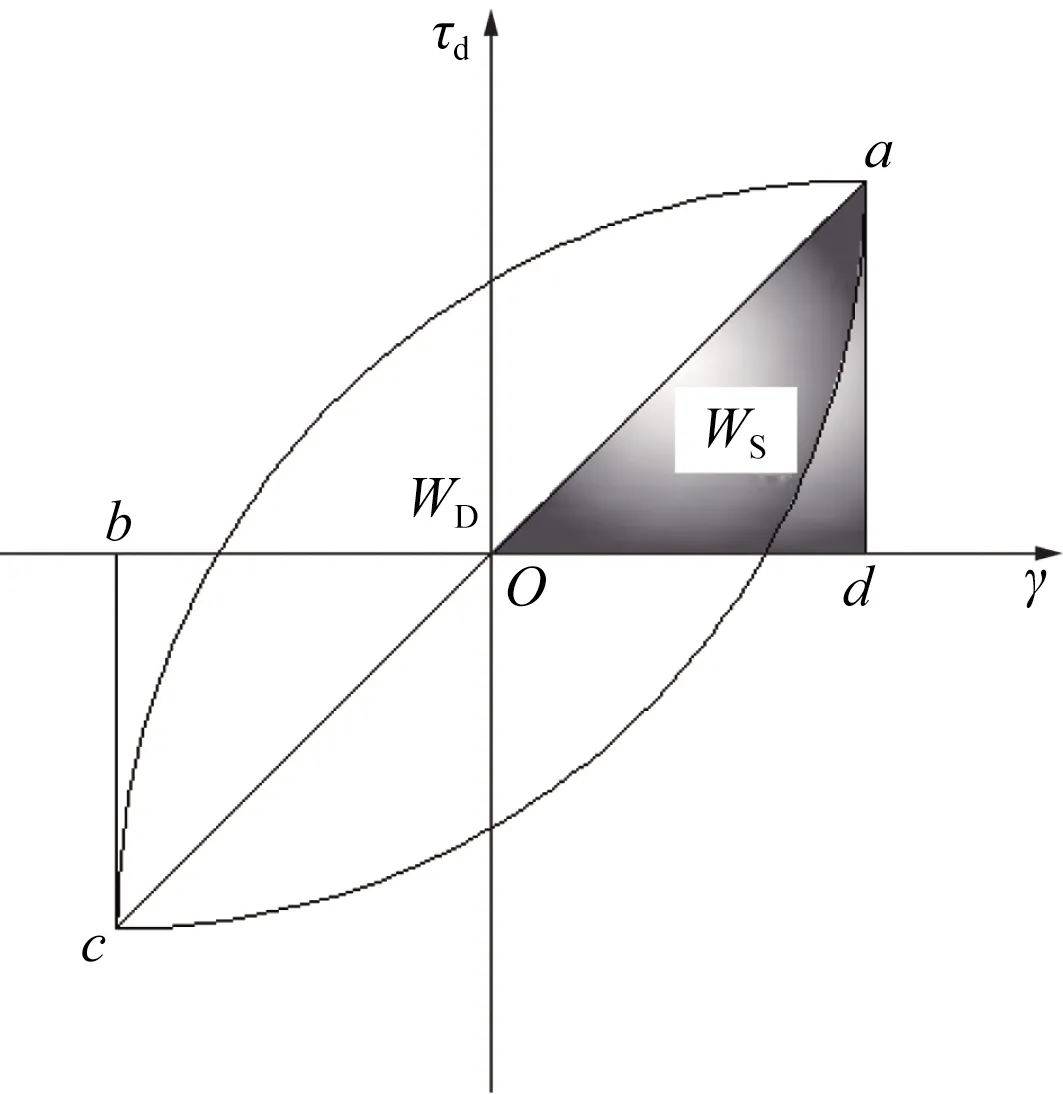
τd為動剪應力幅值；γ為剪應變幅值；點a、c分別為滯回圈的兩個 頂點坐標;點d、b分別為正最大剪應變、負最小剪應變圖1 傳統法Fig.1 Traditional method

1.2 Das法

對一個周期內存儲的應變能進行了修正，如圖2所示，取陰影三角形面積之和的均值為一個周期內儲存的應變能，則阻尼比計算公式為

(3)

式(3)中：WS1、WS2為一個循環周期內存儲的彈性應變能分量。

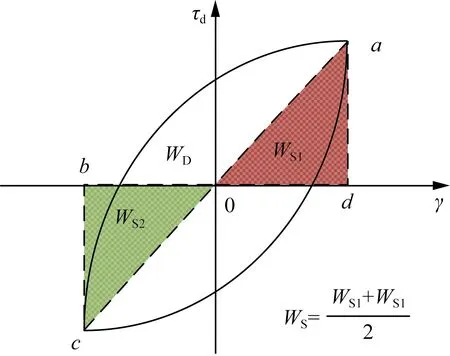
圖2 Das法Fig.2 Das method

1.3 Kokusho法

對一個周期內存儲的應變能進行了修正，如圖3所示，取陰影三角形面積的1/4為一個周期內儲存的應變能，則阻尼比計算公式為

(4)

式(4)中：WS1為Δabc的面積。

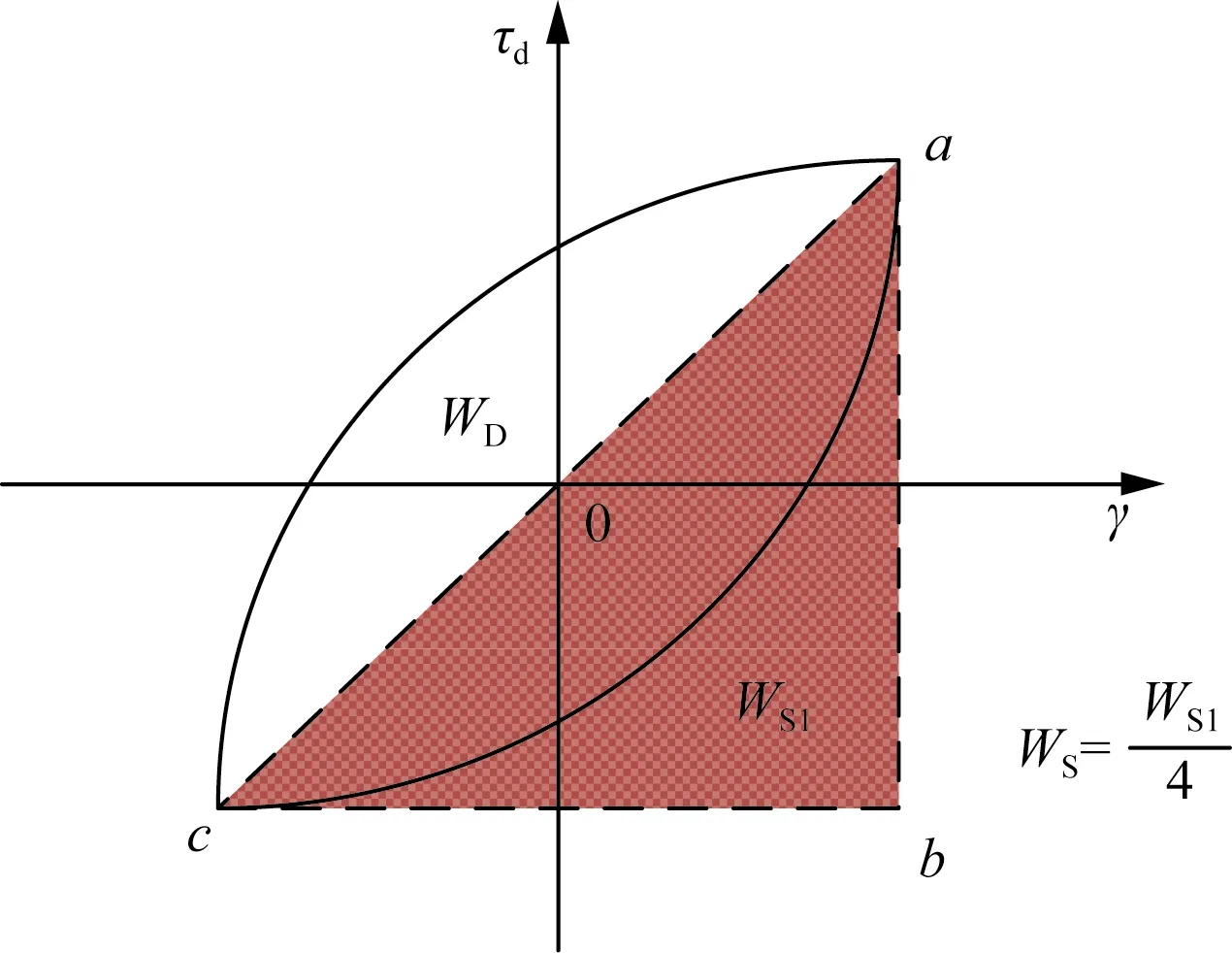
圖3 Kokusho法Fig.3 Kokusho method

1.4 Kumar法

Kumar等對Kokusho法進行修正，如圖4所示，取陰影多邊形面積的1/4為一個周期內儲存的應變

Gmax為最大動剪切模量，MPa；Gsec1為加荷部分的動剪切模量，即滯回曲線正半軸頂點與原點的斜率，MPa；Gsec2為卸荷部分的動剪切模量，圖中為滯回曲線負半軸頂點與原點的斜率，MPa；O點至a點為正向加載階段，a點至b點為正向卸載階段，b點至e點為 反向加載階段，e點至f點為反向卸載階段圖4 Kumar法Fig.4 Kumar method

能，則阻尼比計算公式為

(5)

式(5)中：WS3為一個循環周期內存儲的彈性應變能分量。

1.5 互相關函數法

阻尼比的另一種表達形式是根據耗損系數η來定義的[20]，其表達式為

(6)

(7)

式中：φ為動剪應力、剪應變時程曲線的相位差。

因此只要確定了動剪應力、應變時程曲線的相位差就可以準確的得到阻尼比，梁珂等[18]根據互相關函數的定義，對試驗數據按式(8)處理，得到動剪應力、剪應變時程曲線最大相關性時對應的時間t0(圖5)為

i=0，1，2，…，NN0-i

(8)

式(8)中：Rτγ(iΔt)為第iΔt時刻實測剪應力、剪應變波形的互相關函數值;N0為每周期記錄的試驗點數;N為循環次數;τk、γk+i分別為第kΔt時刻的剪應力試驗值、第(k+i)Δt時刻的剪應變試驗值。

根據互相關函數最大值對應的時間t0計算應力、應變波形的相位差，將式(9)代入式(7)中得到阻尼比計算公式為

φ=ωt0

(9)

(10)

式中：ω為加載頻率。

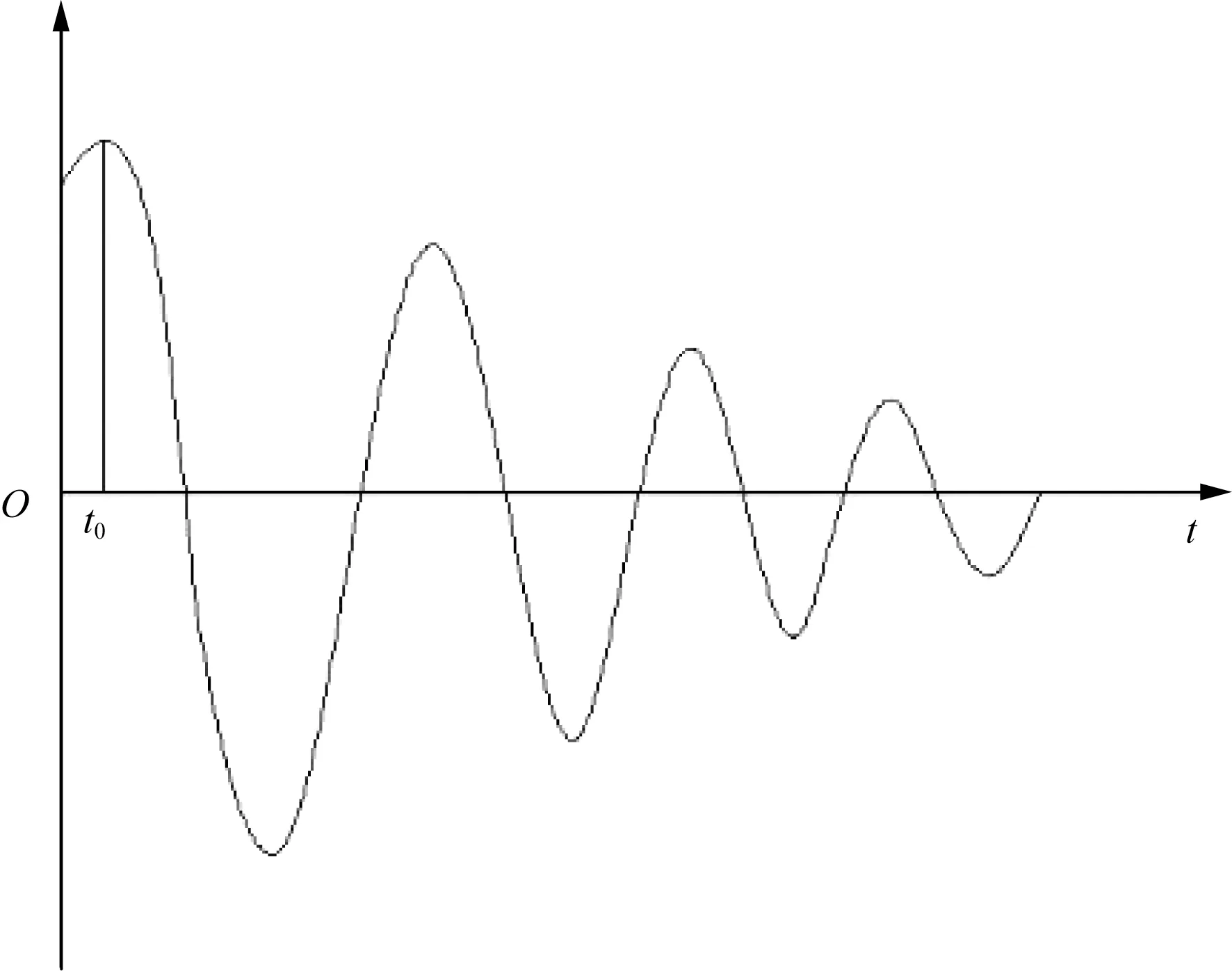
圖5 互相關函數法原理Fig.5 Cross-correlation function method principle

2 室內試驗

2.1 試驗設備

試驗設備采用西安康拓力公司生產的新型電機伺服控制動三軸儀(圖6)，實驗所采用動三軸系統主要性能參數如表1所示。

①為微機；②為數據采集儀；③為伺服控制器；④為壓力室；⑤為力控制器；⑥為試樣；⑦為反壓控制器；⑧為圍壓控制器；⑨為二氧化碳瓶圖6 KTL動三軸儀Fig.6 KTL dynamic triaxial apparatus

表1 KTL動三軸系統主要性能參數Table 1 KTL dynamic triaxial system performance parameters

2.2 試樣

為驗證幾種方法確定阻尼比的差異，采用粒徑為0.5～1.0 mm的福建標準砂作為研究材料(圖7)，以驗證幾種方法確定的阻尼比的差異性。動三軸儀試驗參照《土工試驗方法標準》[21](GB/T 50123—2019)進行操作，所制備試樣直徑為50 mm，高度為100 mm。福建標準砂的基本物性指標如表2所示。

2.3 試驗方案

試驗采用應力控制、多級加載方式，應力由小到大逐級加載。加載波形采用正弦波，加載頻率為1 Hz。采用相對密實度Dr為30%、60%、80%的土樣分別進行試驗。

砂樣制備直接在動三軸儀上完成，采用干砂裝樣法裝樣，共分5層均勻制樣，嚴格控制每層厚度為20 mm；試樣飽和采用先通30 min二氧化碳置換試樣孔隙中的空氣，然后通入無氣水進行水頭飽和，水頭飽和完成后采用分級反壓飽和方式進行土體飽和，當試樣孔壓參數B達到0.95以上，認為試樣飽和度達到要求。

采用等壓固結方式固結，試樣固結壓力分別為100、300和500 kPa，具體試驗方案如表3所示。

圖7 福建標準砂(粒徑0.5～1.0 mm)顆粒電鏡掃描Fig.7 Scanning electron microscope of Fujian standard sand (particle size 0.5～1.0 mm)

表2 試樣基本物性性質Table 2 Basic physical properties of samples

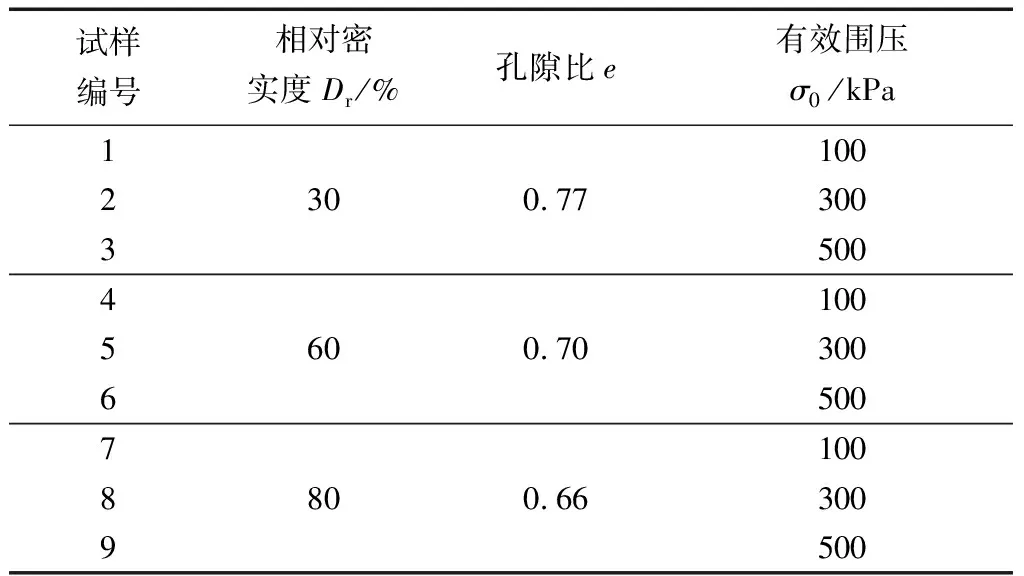
表3 試驗方案Table 3 Test plan

3 阻尼比計算結果

3.1 5種方法計算結果對比

圖8～圖10給出了傳統法、Das法、Kokusho法、Kumar法和互相關函數法5種方法確定的阻尼比。

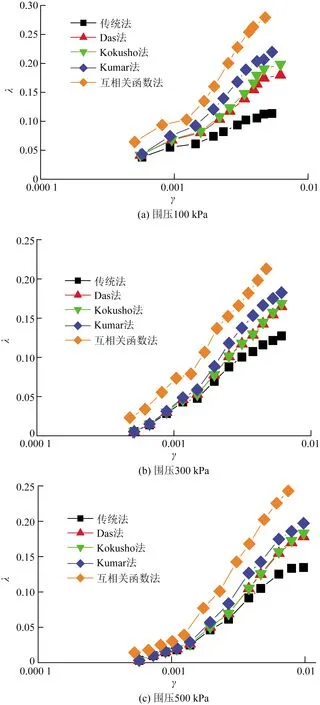
圖8 Dr=30%時不同圍壓下阻尼比-剪應變曲線Fig.8 Damping ratio-shear strain curve of different confining pressures when Dr=30%

圖9 Dr=60%時不同圍壓下阻尼比-剪應變曲線Fig.9 Damping ratio-shear strain curve of different confining pressures when Dr=60%

從圖8～圖10可以看出：剪應變小于10-3時，傳統法、Das法、Kokusho法、Kumar法這4種方法確定的阻尼比基本一致，互相關函數法確定的阻尼比比其他4種方法較大，但隨著有效圍壓的增大互相關函數法確定的阻尼比與另外4種方法確定的阻尼比的差值在逐漸減小；剪應變大于10-3時，隨著剪應變的增大，5種方法確定的阻尼比差值在逐漸增大；互相關函數法確定的阻尼比最大，其他4種方法確定的阻尼比由大到小依次是Kumar法、Das法、Kokusho法、傳統法。有效圍壓較低時，Das法在剪應變大于3×10-3時確定的阻尼比比Kokusho法小，隨有效圍壓增大，兩者確定的阻尼比逐漸趨于一致。

3.2 差異性

為了更直觀地評價各種方法的優劣，采用相對誤差作為評價指標，計算公式為

(11)

式(11)中：δ為相對誤差；λ為阻尼比；λavg為平均阻尼比。

圖11～圖13給出了傳統法、Das法、Kokusho法、Kumar法和互相關函數法5種方法確定的阻尼比的相對誤差。

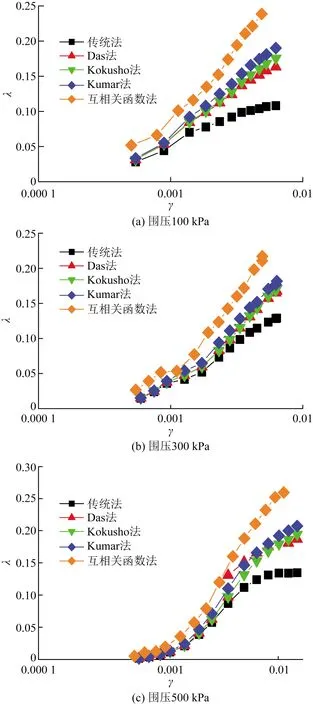
圖10 Dr=80%時不同圍壓下阻尼比-剪應變曲線Fig.10 Damping ratio-shear strain curve of different confining pressures when Dr=80%

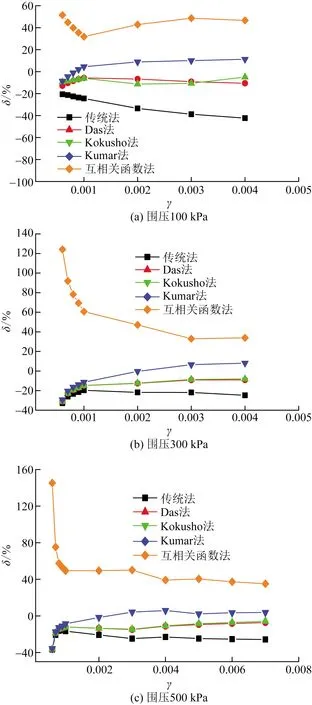
圖11 Dr=30%時不同圍壓下相對誤差-剪應變曲線Fig.11 Relative error-shear strain curve of different confining pressures when Dr=30%

從圖11～圖13可以看出：當剪應變小于10-3時，隨著剪應變的增大5種方法確定的阻尼比相對誤差在迅速減小，當剪應變大于10-3時，減小趨勢緩慢并趨于穩定。

互相關函數法確定的阻尼比遠大于平均阻尼比，并且，最大相對誤差基本都出現在第一級荷載下，隨有效圍壓的增大而逐漸增大；Kumar法確定的阻尼比最接近平均阻尼比，在剪應變小于10-3時，低于平均阻尼比，剪應變大于10-3時，高于平均阻尼比；Das法和Kokusho法確定的阻尼比基本一致，低于平均阻尼比；傳統法確定的阻尼比遠低于平均阻尼比。

3.3 分析討論

分析前述試驗結果，5種阻尼比確定方法產生差異性的原因是：阻尼比是由每周的能量耗損與儲存的彈性應變能之比來確定的，滯回圈法確定的每周能量耗損都為剪應力-應變滯回曲線圍成的面積，但是對存儲的彈性應變能確定方法不同。傳統法計算的儲存應變能為第一象限三角形的面積，未考慮在大剪應變下滯回曲線不對稱的情況，計算結果最大，Das法、Kokusho法考慮了大剪應變下滯回曲線的不對稱性，計算的儲存應變能比傳統法小，而Kumar法是對Kokusho法進行了修正，計算的存儲應變能比Kokusho法小；滯后角法則是根據剪應力應變時程曲線的時間相位差來確定阻尼比。

在實際工程應用時，如果采用應力控制加載，確定阻尼比采用Kumar法比較可靠，主要由于5種確定阻尼比的方法中，Kumar法確定的阻尼比最接近平均阻尼比。

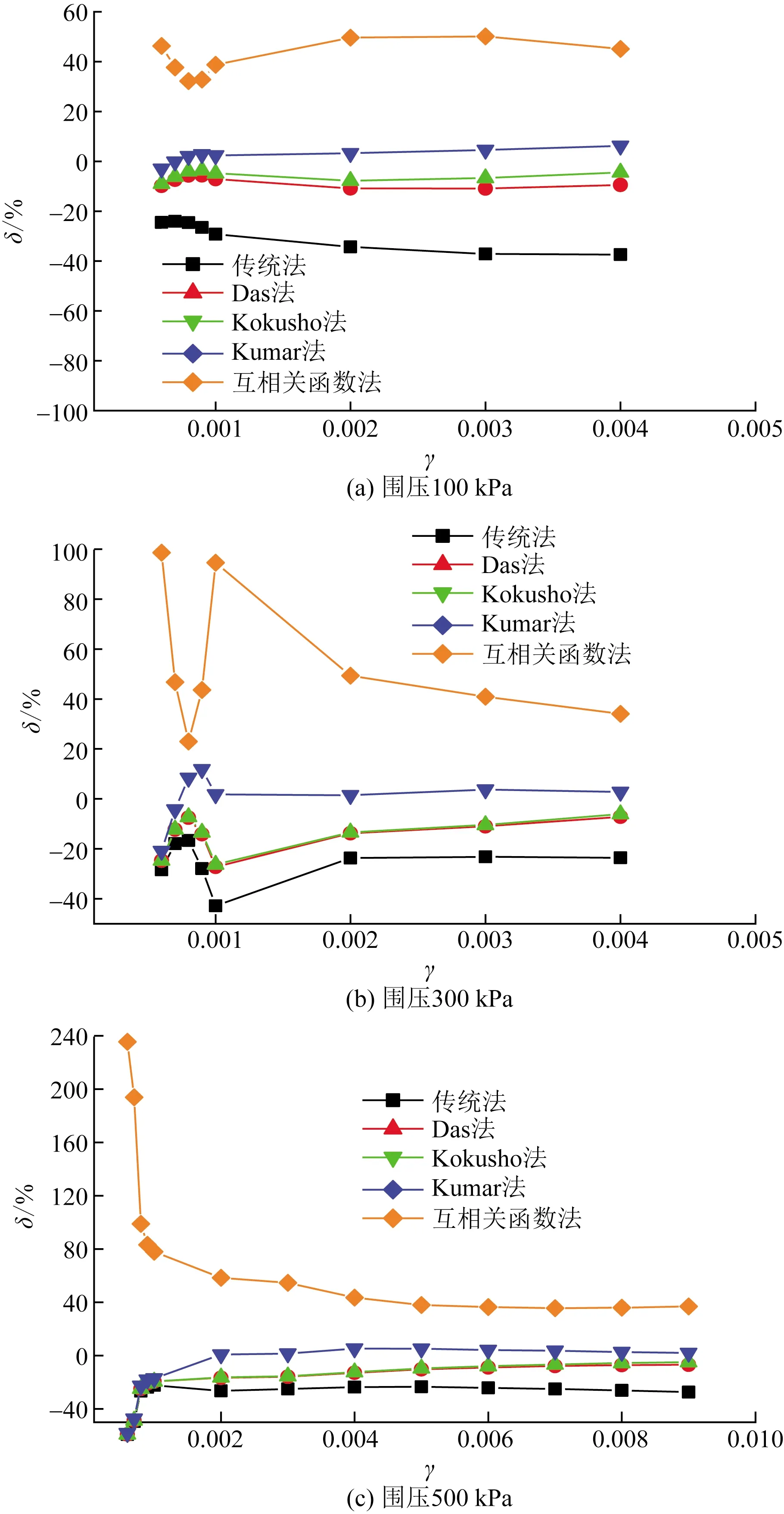
圖12 Dr=60%時不同圍壓下相對誤差-剪應變曲線Fig.12 Relative error-shear strain curve of different confining pressures when Dr=60%

圖13 Dr=80%時不同圍壓下相對誤差-剪應變曲線Fig.13 Relative error-shear strain curve of different confining pressures when Dr=80%

4 結論

通過分析對比5種阻尼比確定方法及其差異性，主要得出以下結論。

(1) 總體上，傳統法、Das法、Kokusho法、Kumar法和互相關函數法確定的阻尼比差異性較大。

(2) 當剪應變小于10-3時，隨著剪應變的增大5種方法確定的阻尼比相對誤差在迅速減小，當剪應變大于10-3時，減小趨勢緩慢并趨于穩定。

(3) 互相關函數法確定的阻尼比最大，其次另外4種方法確定的阻尼比由大到小依次是Kumar法、Das法、Kokusho法、傳統法，其中Kumar法確定的阻尼比最接近平均阻尼比。

(4) 建議采用應力控制加載時，確定阻尼比采用Kumar法，主要由于5種確定阻尼比的方法中，Kumar法確定的阻尼比最接近平均阻尼比。