渦輪增壓器葉片高低周疲勞壽命特性

崔璐， 劉陽， 王澎， 羅浩， 魏文瀾， 李臻

(1. 西安石油大學機械工程學院， 西安 710065； 2. 蜂巢動力系統(江蘇)有限公司， 鎮江 212214)

相對于傳統的自然吸氣式發動機，集成渦輪增壓技術的發動機在不改變排氣量的情況下可以提高輸出功率和扭矩，降低油耗，被認為是經濟有效的“節能減排”方法[1-3]。渦輪增壓器葉片在服役過程中承受由離心力引起的低周疲勞和由振動載荷引起的高周疲勞[4-6]。目前，增壓器壽命和可靠性設計通常采用加大安全系數的方式來考慮高低周疲勞交互作用所引起的損傷。雖然選取了相對保守的安全系數，然而由于疲勞引起的渦輪增壓器的失效案例比例仍高達49%[7]。低周疲勞所引起的葉片損傷、斷裂部位一般為葉片與輪轂的交接部位，高周疲勞所引起的風險區域一般在葉片上，在不利的情況下兩者的位置可能會形成疊加。葉片斷裂會直接導致增壓器總成失效無法修復，斷裂后的葉片甚至可能進入發動機氣缸，造成更大的經濟損失。為了更加真實地預測渦輪葉片的實際壽命，需要考慮渦輪葉片低周疲勞、高周疲勞的交互作用，分析高低周疲勞損傷影響因素，對渦輪葉片進行壽命評估。

通過分析不同因素對高低周疲勞壽命的影響，前人建立了不同的壽命分析模型。崔璐等[8-9]通過對汽輪機轉子材料10Cr-1Mo-1V鋼在高低周疲勞載荷下的應變壽命特性分析發現，高低周疲勞應變幅比與壽命比在雙對數坐標下呈冪函數關系，基于此冪函數關系提出了一種新的高低周疲勞壽命計算方法，并引入四種材料進行驗證，所得結果與實驗值擬合度較高。石欣桐等[10]通過進行LY12CZ鋁合金兩級疲勞載荷實驗，分析載荷加載順序的先后對壽命的影響，并基于多機制耦合損傷模型建立了考慮加載順序的壽命預測模型，并將預測壽命與Miner模型預測值對比，結果顯示較Miner模型預測值更為精確。李洪松等[11]將低幅高周載荷對復合損傷的弱化作用考慮在內，引入弱化函數建立具有低載強化效應的高低周疲勞壽命預測模型。

對于葉片結構承受高低周復合疲勞載荷的情況，張亞騤等[12]在壓氣機葉片復合疲勞實驗系統的設計及疲勞壽命分析中，保持葉片低周應力不變，改變高周應力幅值，得到高周應力(即高低周疲勞中高周應力比RHCF，σ)與高低周疲勞壽命呈雙對數線性關系。閆曉軍等[13]在渦輪葉片復合疲勞特性實驗中，保持葉片低周應力不變，改變葉尖振動應力得到RHCF，σ與高低周疲勞壽命成雙對數線性關系，并用同樣的實驗方法分別對幾何結構完全相同的GH4133合金葉片，形狀類似、尺寸不同的 K403合金、DZ22B合金葉片進行上述疲勞實驗，也得到相同結論。說明上述雙對數線性規律與葉片的材料、尺寸無關，對于鎳基高溫合金葉片普遍適用。

高低周疲勞實驗中，當低周應力不變時，單個高低周復合載荷塊中高周循環次數n越大，達到峰值應力的次數越多，壽命減少越明顯。李睿等[14]在對2024-T3鋁合金進行高低周疲勞實驗時，保持低周應力以及疊加的高周應力不變的情況下，改變高周循環次數n，隨著高周循環次數n的增加，其高低周疲勞壽命顯著降低，并得到復合載荷塊中高周循環次數n與高低周疲勞壽命呈雙對數線性關系。王時越等[15]對45鋼制成的標準試樣采取控制應力方法，在梯形波上加載高周正弦波進行高低周疲勞實驗，得出高周循環次數n近似與高低周復合疲勞壽命成雙對數線性關系，以上分析說明對于不同的金屬材料，其高低周疲勞壽命均會受到高周循環次數n、高低周疲勞中高周應力比RHCF，σ的影響。

以上研究表明，高低周復合疲勞壽命預測模型的建立是高低周復合疲勞損傷的重點。因此，現通過研究所疊加高周循環數n和高低周疲勞中高周應力比RHCF，σ對材料疲勞壽命的影響，建立基于Miner理論的高低周疲勞壽命預測模型。借助有限元對渦輪葉片進行分析，建立考慮固有頻率、共振等因素的高低周疲勞分析模塊，對壽命修正模型進行驗證。

1 高低周疲勞壽命預測模型的建立

高低周復合載荷下的損傷D可表述為低周疲勞損傷DLCF和高周疲勞損傷DHCF的線性疊加[16-17]，表達式為

D=DLCF+DHCF

(1)

若高周和低周均為周期性等幅載荷，則D可表示為

(2)

式(2)中：n為一個低周循環內的高周循環次數；NHCF為純高周疲勞壽命；NLCF為純低周疲勞壽命；m為D時所經歷的高低周疲勞載荷塊個數。高低周載荷譜為在低周載荷譜保載階段疊加n個高周循環載荷所組成的復合載荷譜，如圖1所示。此模型中，將高周疲勞和低周疲勞損傷簡單累加，沒有考慮到二者之間的交互作用。為考慮高低周交互作用所帶來的耦合損傷，擬采用高低周疲勞采用高低周疲勞中高周應力比RHCF，σ[18]作為分析損傷的影響因素。

Δσtotal為總應力范圍；Δσminor為高周應力范圍；Δσmajor為低周應力 范圍；σLCF為低周疲勞載荷塊中低周應力圖1 高低周疲勞載荷譜示意圖Fig.1 High and low cycle fatigue load spectrum diagram

高低周疲勞中高周應力比RHCF，σ可表示為

(3)

當低周循環周期內疊加的高周載荷僅在保載時段內，同時高周作用次數n較低時，高周疲勞對高低周復合疲勞壽命的影響可忽略不計[11]。若低周保載時長不變，則高低周疲勞中高周應力比RHCF，σ、單個高低周載荷譜中高周作用次數n是影響高低周疲勞壽命的主要因素[13，18-21]，兩者與高低周疲勞壽命NLCF+HCF的關系如圖2和圖3所示。在低周應力固定為470 MPa，高周作用次數n=20，高周頻率f=20 Hz時，高低周疲勞壽命與高低周疲勞中RHCF，σ的關系如圖2所示。在RHCF，σ<0.9時，隨著RHCF，σ的增大，高低周疲勞壽命呈線性增長。當RHCF，σ為0.9～1時，壽命發生突增，由于此時疊加的高周應力與高低周疲勞載荷中低周應力接近，使得此時的高低周疲勞相當于純低周疲勞，從而導致壽命突增。

圖2 NLCF+HCF隨RHCF，σ的變化規律[15]Fig.2 NLCF+HCF changing with RHCF，σ[15]

圖3 NLCF+HCF隨n的變化規律[15]Fig.3 NLCF+HCF changing with n[15]

當低周應力同為470 MPa且恒定時，同時保持RHCF，σ=0.3和f=20 Hz不變，高低周疲勞壽命與復合載荷譜中所疊加的高周作用次數n呈單對數線性關系(圖3)。當n取較大值且隨著n的增大，壽命快速下降。當高周作用次數n較小值時(n<100)，隨著n的增大，壽命變化較小。總體上高周應力比RHCF，σ對壽命的影響較大。

若將高低周復合疲勞載荷譜拆分成低周疲勞載荷塊和高周疲勞載荷塊(由n個高周循環組成)，如圖1所示。其中，高周疲勞載荷塊的平均應力為低周保載應力。在相同的高周頻率作用下，高周應力Δσminor/2(圖1中Δσminor)循環加載時所對應的純高周疲勞壽命為NHCF，以每n個高周次數為一組將其換算成高周疲勞載荷塊循環數NHCF，b=NHCF/n。此時，純高周疲勞載荷塊循環數NHCF，b與包含n個高周循環的高低周復合疲勞壽命NLCF+HCF的差值為Nc，即純低周疲勞和高低周耦合損傷引起的壽命會縮短。

圖4 Nc隨RHCF，σ的變化規律Fig.4 Nc changing with RHCF，σ

表1 TC11鈦合金高低周疲勞實驗數據Table 1 TC11 titanium alloy high and low cycle fatigue experiment data

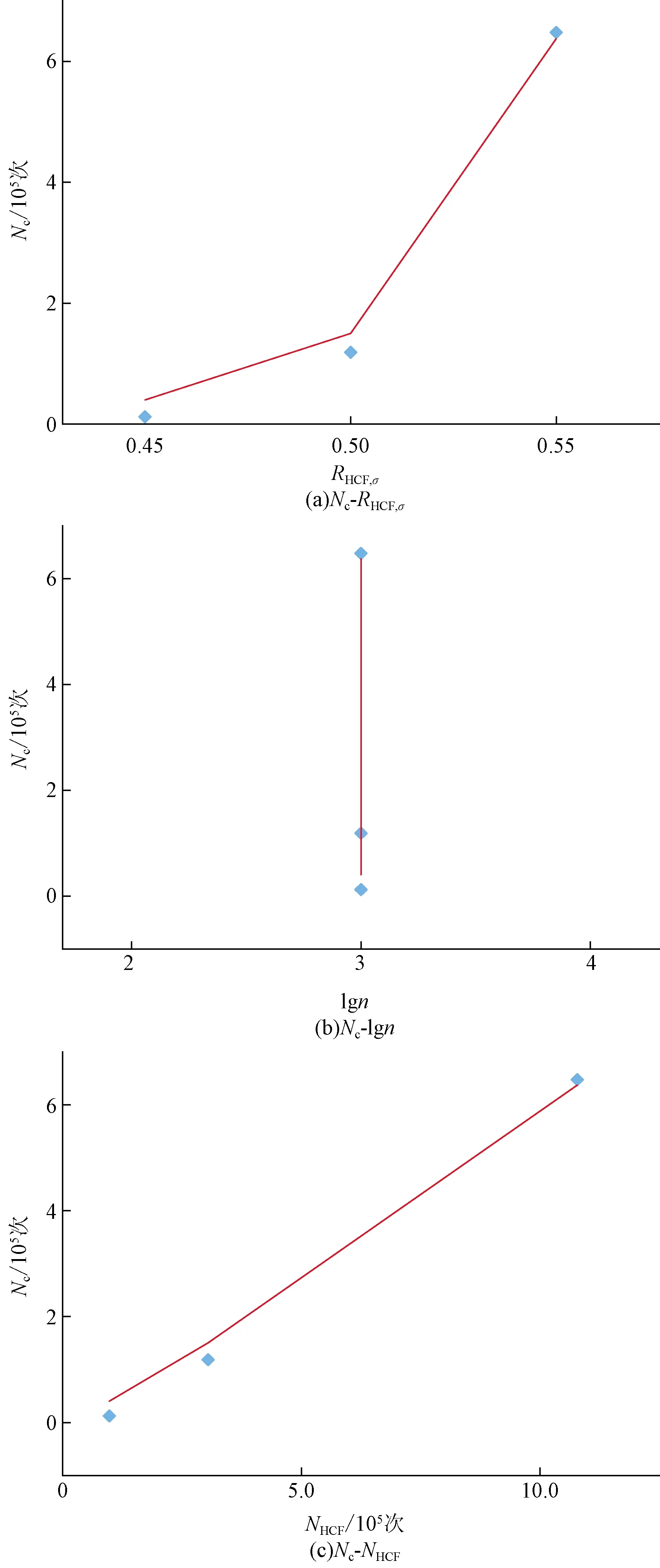
圖5 低周保載應力為750 MPa時Nc與各變量擬合曲線Fig.5 Fitting curves of Nc and various variables when the low cyclic retaining stress is 750 MPa

圖6 低周保載應力為800 MPa時Nc與各變量擬合曲線Fig.6 Fitting curves of Nc and various variables when the low cyclic retaining stress is 800 MPa

根據圖5、圖6的擬合結果，低周保載應力為750 MPa時，擬合得參數B為36.985，相關性系數R2=0.991，擬合度較好。當低周保載應力為800 MPa時，擬合得參數B為14.963，相關性系數R2=0.931，擬合度并不十分精確。由于參數B不能很好地反映材料特征，考慮不同組實驗所位于的低周保載應力不同，也就是平均高周應力值不同，因此引入低周保載應力對參數B進行優化，修正為

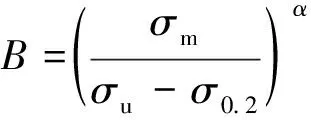
(4)

式(4)中：σm為高周應力的平均值，即高低周載荷譜中低周幅值應力；α為與材料相關的系數；σu、σ0.2分別為材料抗拉強度、屈服強度。純低周疲勞和高低周耦合損傷引起的壽命縮短值Nc可表示為

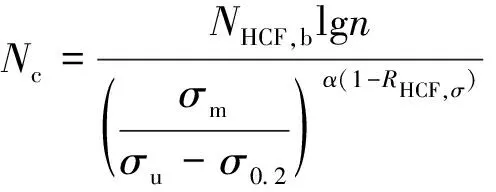
(5)

式(5)中：材料相關系數α一般取2～9，對于TC11鈦合金，α取2.5。

由Miner疲勞準則可知，由低周疲勞和高低周耦合所引起的損傷為Nc/NHCF，b，設N為高低周疲勞載荷循環數，則此時單個高低周疲勞載荷塊中高低周耦合作用、低周疲勞作用所造成的損傷Dc為

(6)

由于此處采用N所推得模型求解值與實際值有差距，為精確求解，采用與N在相同數量級且相差不多的NHCF代替N(后用所推模型代入反算，證實合理性)，將Nc代入式(6)可得

(7)

通常單個高低周疲勞載荷塊中高周疲勞作用產生損傷應為n/NHCF，b，高低周疲勞中單個復合載荷塊中高周作用產生損傷則為1/NHCF，b。將高低周復合載荷塊中單純高周疲勞所引起的損傷與低周疲勞、高低周耦合作用的損傷Dc疊加，記作D，表達式為

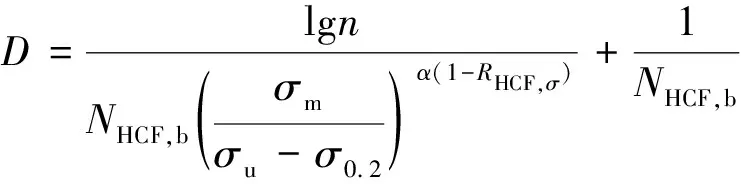
(8)

高低周復合疲勞壽命的估算公式為

NLCF+HCF=

(9)

式(9)中：NLCF+HCF也即高低周疲勞載荷塊的個數，即為所求高低周疲勞壽命。

前面為利于計算，將式(6)中N用NHCF代替，因此將TC11實驗數據帶入壽命修正模型進行反算驗證式(6)合理性。如表2、圖7所示，利用新擬合模型所得高低周疲勞載荷塊個數NLCF+HCF與實驗值擬合度較高，除低周應力為750 MPa，RHCF，σ= 0.5時所求壽命大于實驗值，其余壽命均小于實驗值，模型可用。

利用修正模型對TC11 材料高低周復合疲勞實驗壽命進行預測[19]，結果如表3所示，線性Miner模型預測壽命較為保守，而修正好的模型預測壽命較為準確，與實驗結果的誤差在2倍范圍以內(圖7)。當RHCF，σ=0.2、n=200時，高低周交互作用反而造成了疲勞壽命的增加，原因可能是低周疲勞對高低周疲勞有減緩作用。

表2 TC11鈦合金高低周疲勞壽命預測Table 2 TC11 titanium alloy high and low cycle fatigue life prediction

圖7 高低周復合疲勞壽命預測值與實驗值對比Fig.7 Comparison between predicted and experimental values of high and low cycle composite fatigue life

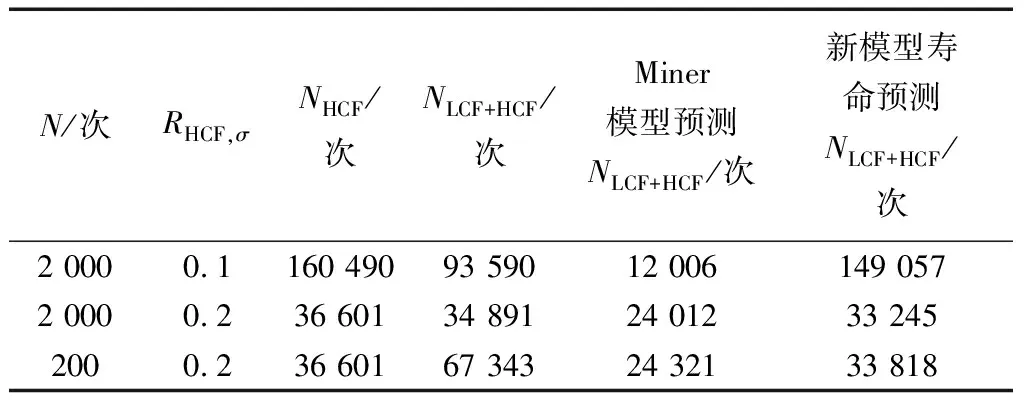
表3 高低周疲勞壽命預測結果Table 3 High and low cycle fatigue life prediction results

2 渦輪葉片高低周疲勞特性分析

2.1 有限元分析設置

2.1.1 材料屬性設置

分析所用渦輪葉片材料為鎳基合金K418[20-21]，由于實際工況下渦輪葉片的溫度場分布非常復雜，且考慮到鎳基合金材料常溫下至700 ℃的力學性能變化不大，故采用室溫下的力學性能參數，如表4所示。

表4 K418鎳基合金室溫下力學性能Table 4 Mechanical properties of K418 nickel-based alloy at room temperature

2.1.2 網格劃分

將渦輪葉片幾何模型導入關聯Workbench與可兼容版本的Creo三維制圖軟件。由于渦輪幾何較為復雜，因此采用能夠適應模型復雜、扭曲度較大的三維四面體網格。為保證計算精度的同時提高計算效率，且考慮危險部位一般位于葉片與輪轂交接處、過渡圓角等部位，因此對該部分采用面網格進行細化，細化尺寸為0.08 mm，其余非關鍵部位采用體網格，網格尺寸為0.5 mm，最終網格如圖8所示，所得網格單元數為1 015 079，網格節點數為1 492 061，網格平均質量0.819>0.7，整體網格質量良好。

圖8 葉輪網格劃分Fig.8 Impeller meshing

2.1.3 邊界條件與載荷

渦輪葉片所受到的低周應力主要由離心載荷和溫度載荷共同引起，由于增壓器實際工況中持續高溫工作的時間較短，此時可不考慮蠕變損傷。為模擬渦輪真實運行工況，采用整渦輪分析(或將渦輪沿軸心12等分葉片，沿徑向兩截面設置循環對稱約束[17，22])，在渦輪上下端面施加固定端約束給予軸向固定(給予軸向約束，切向、徑向所在平面平動約束)，如圖9、圖10所示。目前渦輪增壓器轉速通常工況選取轉速160 000 r/min，通過給定轉速充當離心力載荷。

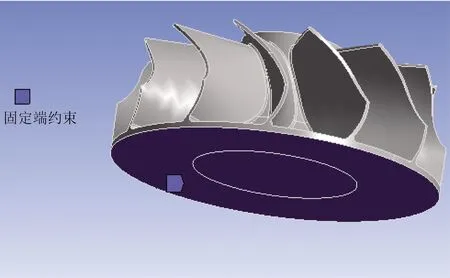
圖10 固定端約束施加Fig.10 Fixed end constraints imposed

2.2 模擬結果與分析

2.2.1 應力分布

當轉速為160 000 r/min時，所得渦輪葉片應力大小及分布如圖11和圖12所示，圖11為最大應力部位局部放大圖。可以看出，輪轂內部、葉片后蓋板處所受應力較小，從葉片前緣至葉片根部應力逐漸增大，渦輪葉片風險部位在葉片與輪轂的上端交接處，最大應力798.25 MPa，此應力是由渦輪高速旋轉所產生的離心力在渦輪內部形成向外的拉應力所致，并在輪轂處形成局部高應力區，所得風險部位與渦輪實際工作發生疲勞斷裂的部位相符。風險部位最大應力798.25 MPa >σ0.2=770 MPa，此應力即為渦輪葉片低周應力，渦輪葉片進入屈服狀態，該應力作為模態分析、諧響應分析的預應力，進行應力疊加。

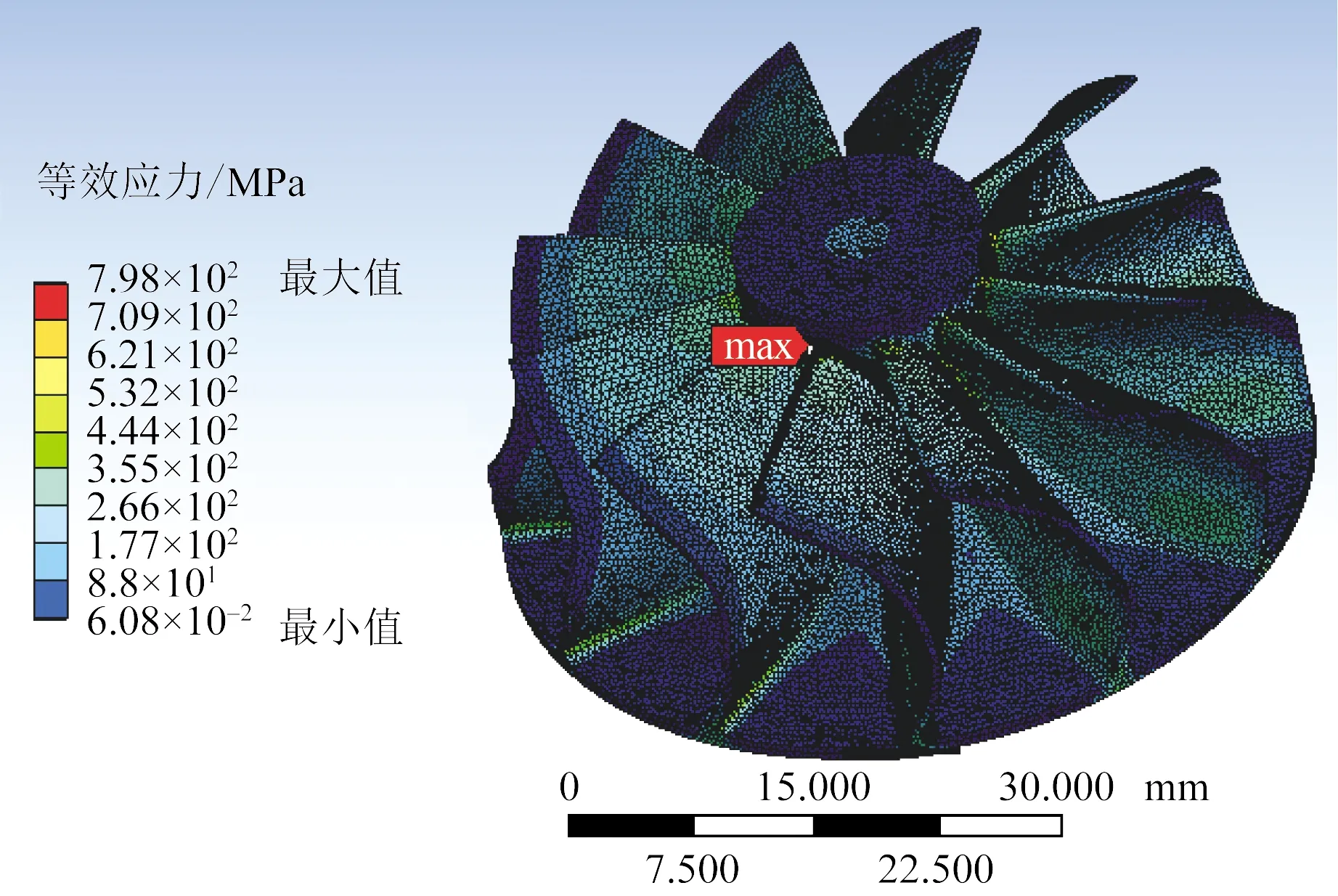
圖11 低周應力分布Fig.11 Low cyclic stress distribution

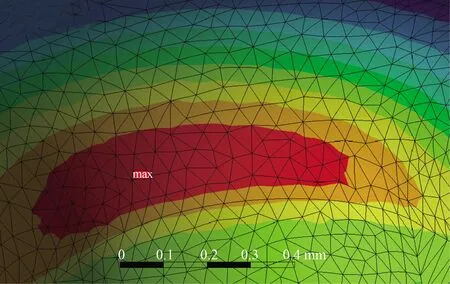
圖12 風險部位Fig.12 Risk area

2.2.2 諧響應分析

由于渦輪增壓器運行時，工況較為復雜且其高周應力值變化較小，目前高周應力值還無法精確測得，因此決定對渦輪進行諧響應分析，即含預應力的高周疲勞分析，確定渦輪上施加的高周應力的取值范圍。K418是鎳基超級合金，耐熱性好，其工作溫度與室溫時的物性參數基本相同，隨時間變化產生的蠕變損傷忽略不計，因此材料模型與時間無關，后面的疲勞計算仍舊忽略時間效應。

當轉速為160 000 r/min且靜態阻尼系數為0.02時，模態分析生成坎貝爾圖[17，23-25]，如圖13所示，渦輪葉片一階固有頻率為14 869 Hz，二階固有頻率為27 869 Hz。轉速在0～2 666 r/s時，前5倍基頻與葉片的一階固有頻率未發生耦合，直到6倍基頻時發生第一次耦合。通常，若4倍基頻線與一階固有頻率線沒有相交，則認為葉片有足夠的安全裕度，不會發生共振[26-27]。因此在渦輪葉片實際工作轉速范圍內，不會由于轉速的變化發生共振。

純高周疲勞不至于使葉片失效，但和低周載荷疊加后，會縮短使用壽命。此次高周應力取值范圍依據葉片共振時的應力響應作為參考(使基頻不斷增加直至共振只為獲得高周應力參考范圍，選取高周應力值，實際并未達到共振)。為獲得高周應力參考范圍，繼續對渦輪葉片進行諧響應分析。基于模態分析中前兩階模態所在區間，使基頻不斷增加直至與二倍固有頻率線相交，取一階共振、二階共振時預應力考核部位的應力響應范圍作為高周應力參考。

圖13 渦輪坎貝爾圖Fig.13 Turbine Campbell diagram

在Harmonic Response模塊中對渦輪葉片表面施加沿切向均布面力激勵，大小為20 N。取激勵頻率范圍0～29 500 Hz進行諧響應分析，考核部位仍為葉片與輪轂的上端交接處，渦輪葉片校核部位應力幅值隨高周頻率的響應如圖14和圖15所示，在渦輪葉片的一階固有頻率13 856～14 869 Hz附近，發生了共振耦合，應力幅值迅速增加，達到94.725 MPa，將此應力值作為高低周載荷譜疊加高周應力的參考，此時的應變響應為0.000 215 mm/mm。在二階固有頻率25 648～27 869 Hz附近，同樣發生了共振耦合，第二次耦合所得應力為48.735 MPa，應變響應為0.000 149 6 mm/mm。由此分析，在考慮高低周疲勞載荷交互作用時，應力幅值及應變響應并非隨高低周載荷譜中高周循環次數n的增加而簡單增加，當作用次數與時間或頻率相關，且加載頻率與葉片固有頻率相近時，應力幅值及應變響應變化異常劇烈。

自此，以有限元分析所得渦輪葉片低周應力為基礎，以諧響應分析高周應力范圍為參考，在Ncode中搭建疲勞分析模塊，在渦輪葉片低周應力考核部位上疊加高周應力，求取高低周疲勞壽命。同時將有限元分析所得低周應力、高周應力范圍代入新建立壽命修正模型，求取高低周疲勞壽命，對比兩種算法的壽命偏差值。

圖14 渦輪應力幅值響應Fig.14 Turbine stress amplitude response

圖15 渦輪應變幅值響應Fig.15 Turbine strain amplitude response

2.2.3 Ncode疲勞計算

將所求渦輪葉片低周應力文件導入Ncode疲勞軟件，并根據諧響應分析結果中應力響應范圍確定高低周載荷譜中疊加的高周應力，載荷譜示意圖如圖16所示。

高低周載荷譜中低周應力σm取798.25 MPa，分別選取諧響應分析中最大應力幅值的5%、10%、20%、30%作為高周應力疊加，即疊加的高周應力分別為4.736、9.473、18.914、28.418 MPa，則RHCF，σ分別為0.989、0.976、0.952、0.937，并且取高低周載荷譜中疊加高周作用次數n=1 000，進行高低周疲勞壽命的求解。

Ncode中對有限元分析所得應力按式(10)進行計算[26]，公式為

(10)

式(10)中：maxk和mink分別為各個載荷歷程中公式系數最大值與最小值，根據有限元計算得出；SFk為比例因子；σeq，k為等效應力；當涉及多種形式的載荷時，會用dk進行修正，一般默認為1。將處理后應力帶入滿足高斯分布的S-N曲線概率密度函數，利用概率密度函數式(11)求得壽命。

(11)

(12)

式中：μ為置信度Φ取0.5時所對應的x值，即均值，置信度越高，所得壽命越低。基于式(11)、式(12)求得x，即lgN。

最終所得壽命云圖如圖17所示，在渦輪葉片入口端由于受激振力影響，使得入口段壽命相比于渦輪葉片其他部分較短，4種高周應力水平下所求得渦輪葉片的高低周疲勞載荷塊NLCF+HCF如表5所示。

圖16 高低周載荷譜塊示意圖Fig.16 High and low load spectrum block diagram

圖17 渦輪葉片疲勞失效時所經歷載荷塊的次數Fig.17 Number of load blocks experienced by turbine blades during fatigue failure

表5 4種高周應力水平下壽命預測結果Table 5 Life prediction results under four high cycle fatigue stress levels

3 高低周疲勞壽命預測模型驗證與對比

修正后的模型求高低周疲勞壽命時需用到高周疲勞載荷塊數NHCF，b，為保證疲勞軟件與新模型所求高低周疲勞壽命一致，高周疲勞載荷塊數NHCF，b采用疲勞軟件所求壽命值。取σm=798.25 MPa，n=1 000(一個載荷譜塊)，分別設置4種高周應力水平下的高周恒幅載荷譜，如圖18所示，求得NHCF，b(換算成與高低周載荷塊一致的量)如表5所示，將高周疲勞載荷塊數NHCF，b代入考慮高低周疲勞交互損傷的新模型中，求得高低周疲勞壽命。

依據上述σHCF，NHCF，b，并取α為4.5(系數α取值范圍的中值)，n=1 000，代入考慮高低周復合損傷的式(9)中求得4種高周應力水平下的高低周疲勞載荷塊數NLCF+HCF如表5、圖19所示。修正模型所得NLCF+HCF隨高周應力幅值的增加呈遞減趨勢，壽命變化較大，經疲勞軟件在應力最大值處(結點527 178)所得壽命隨高周應力幅值的增加同樣呈遞減趨勢，相比于修正模型壽命變化較小。如圖19所示，Ncode預測壽命與修正模型預測壽命較為接近，誤差在2倍范圍之內。修正模型所得預測壽命值較小，相比于Ncode預測壽命，較為保守。其次，求高低周載荷譜中σHCF相同、疊加的不同n時，疲勞軟件與修正后模型所得壽命變化。取諧響應分析中最大應力幅值的30%作為高周應力疊加，n分別取100、500、1 000和2 000時，所得壽命如表6、圖20所示。可以看出，Ncode所得壽命較大，壽命呈遞減趨勢；修正模型所得壽命較小，壽命同樣呈遞減趨勢；兩種方式所得壽命較為接近，誤差在2倍范圍之內。造成壽命偏差原因在于軟件內部公式對高低周載荷譜中高周應力值變化不敏感，主要考慮低周應力并沒有考慮高低周交互損傷，使得壽命值隨高低周復合疲勞、復合載荷塊中n的變化降低較少，所得高低周疲勞壽命值較大。

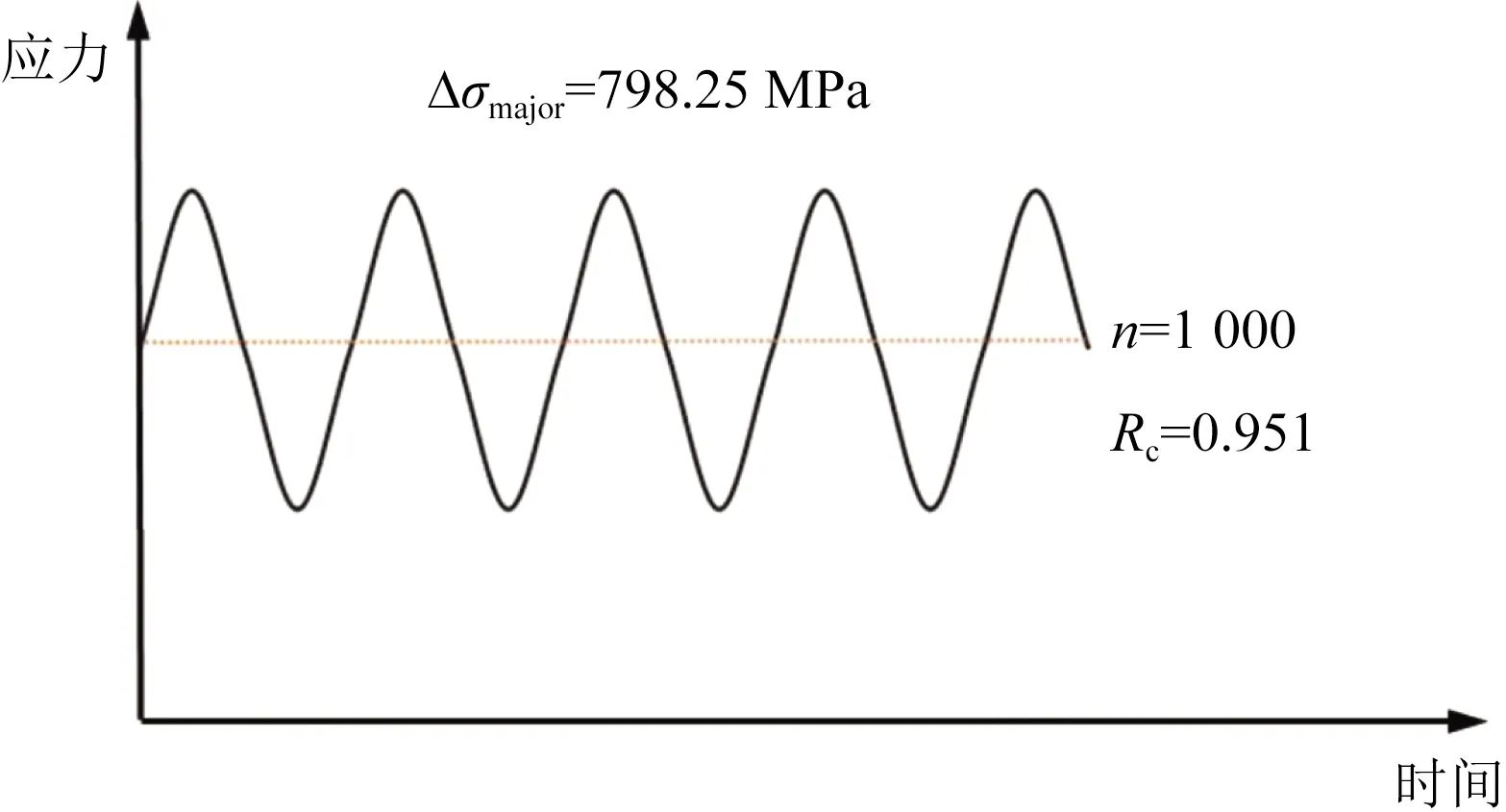
圖18 高周恒幅載荷譜Fig.18 Constant amplitude load spectrum of high cycle fatigue

圖19 4種高周應力水平下壽命預測Fig.19 Life prediction results under four high cycle fatigue stress levels

對于修正模型而言，首先，α尚未經過大量實驗數據擬合和驗證，取值為現有文獻的估計值；其次，高低周復合疲勞、復合載荷塊中n與渦輪壽命的擬合還不夠充分；另外，由于該模型目前為止僅涉及少數幾種材料，因此針對不同渦輪材料α的取值仍需進一步研究。對于渦輪增壓器廠商和主機廠而言，由于其擁有足夠的臺架實驗數據和路測數據，上述模型參數的確定可以通過簡單的回歸分析實現，從而可以獲得更精確的壽命分析結果。

表6 4種n值下壽命預測結果Table 6 The life prediction results under four kinds of the value of n

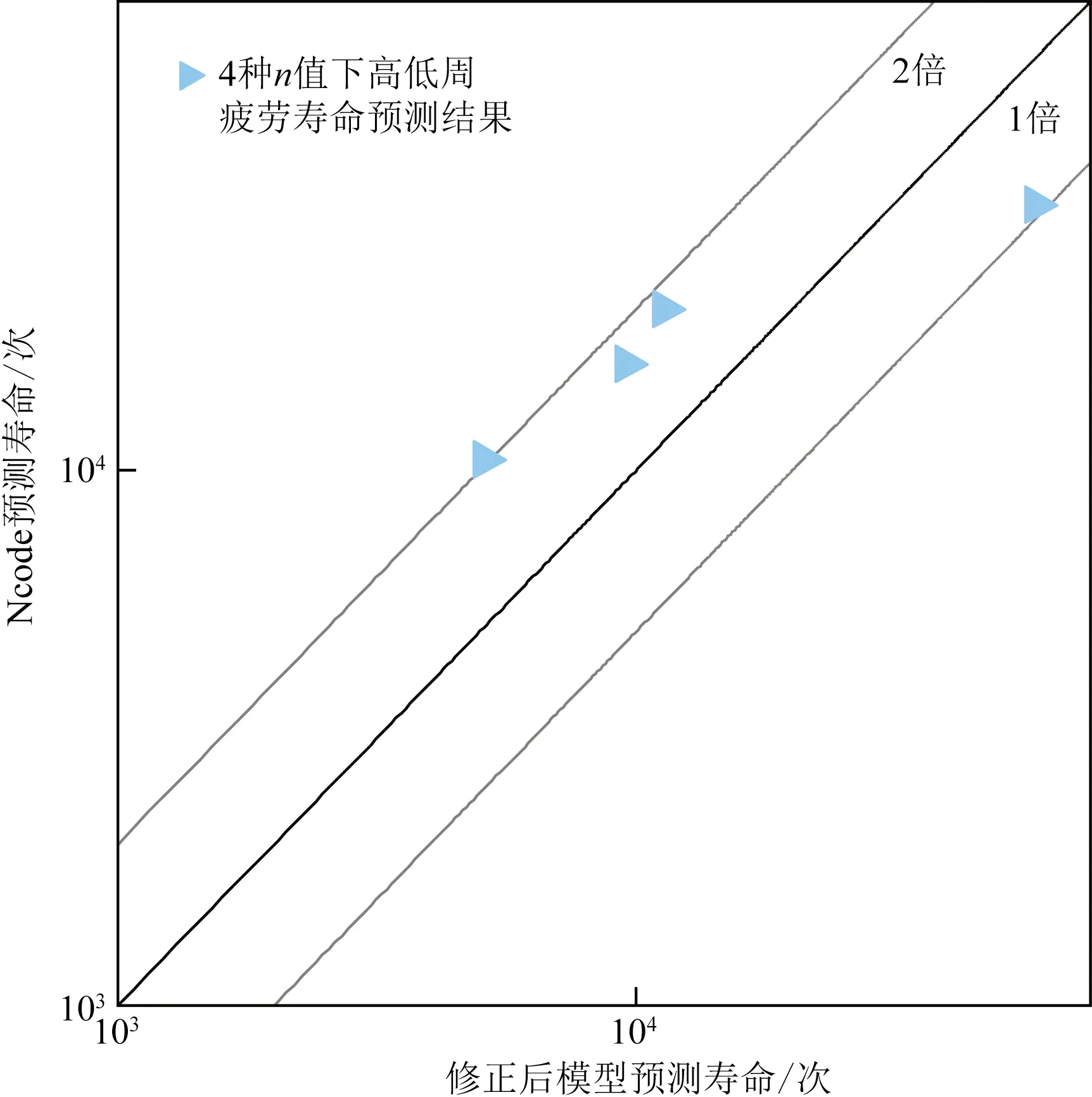
圖20 4種高周疊加次數n值下壽命預測Fig.20 Life prediction under four kinds of high cycle fatigue stacking times n value

商用軟件Ncode操作較為復雜，修正后壽命預測模型引入了RHCF，σ、高低周疲勞載荷塊n，通過擬合高低周疲勞壽命與RHCF，σ、n的關系進而分析高低周疲勞的交互損傷，該算法對于渦輪增壓器渦輪葉片壽命預測結果較為可靠。另外，該模型屬于唯真模型范疇，工程使用較為簡單便捷。

5 結論

(1)以RHCF，σ、n為參數基于Miner理論建立一種高低周疲勞壽命修正模型，并通過有限元模擬對壽命進行了驗證。

(2)通過Workbench平臺對渦輪增壓器渦輪建立了較為完善的高低周疲勞分析體系，當n與時間或頻率相關，且加載頻率與葉片固有頻率接近時，應力幅值變化幅度較大，因此疲勞損傷分析時應考慮共振影響。

(3)應力在屈服極限附近時，壽命對應力值的變化極其敏感，可考慮在屈服極限以下30～80 MPa到抗拉強度之間建立應力分析區間。在高低周復合疲勞載荷譜中，當高周應力與低周應力非常接近時，低周疲勞對高低周疲勞有減緩作用。

(4)商用軟件Ncode操作較為復雜，與修正模型相比，其內部公式對于高低周疲勞沒有考慮高低周交互損傷，所得壽命較大；而修正模型所得壽命較為保守。對于渦輪增壓器渦輪葉片壽命計算，可用修正模型求得高低周疲勞壽命。