基于改進麻雀搜索算法-核極限學習機耦合算法的滑坡位移預測模型

馬飛燕， 李向新

(昆明理工大學國土資源工程學院， 昆明 650093)

滑坡是一種由于自然環境變化或人類活動改變了邊坡平衡狀態后引起的地質現象。突發性的山體滑坡會造成巨大的生命和財產損失[1]。由此，對滑坡變形進行預測預警[2-3]越來越重要，多年來，研究人員將滑坡預測模型分為物理模型和數據驅動模型兩大類[4]。

數據驅動模型相較物理模型強調根據以往的實測數據建立相關的數學模型進行預測。在影響滑坡穩定性的因素眾多[5]，滑坡變形的物理機理比較復雜的情況下，數據驅動模型有著較好的預測精度。而隨著計算機技術的發展，以神經網絡模型[6]、支持向量機模型[7]、極限學習機模型[8]為代表的數學模型，由于對類似復雜條件下的滑坡體變形這樣的非線性復雜系統行為[9]預測方面有著較好的準確性，逐漸成為數據驅動滑坡預測的研究熱點。支持向量機和最新發展起來的極限學習機則克服了傳統神經網絡模型易造成局部最優的缺點，得到了大范圍的推廣與應用。同時，范千等[10]發現，加入小波變換后的預測模型對滑坡位移的預測更加準確，小波變換從而被大范圍應用于滑坡的位移預測[9， 11-14]。

基于以上研究背景，以阿海水電站附近某滑坡獲得的全球定位系統(global positioning system，GPS)監測數據為例，首先將滑坡累計位移進行小波分解處理，將位移數據分解為趨勢項位移和周期項位移，應用核極限學習機(kernel-based extreme learning machine，KELM)對各分項位移進行預測，并使用麻雀搜索算法(sparrow search algorithm， SSA)對核極限學習機的各項參數進行尋優，最后將趨勢項位移和周期項位移相加得到最終預測結果。將預測結果與支持向量機模型做對比，以均方根誤差、平均相對誤差絕對值和相關性系數三項指標評價滑坡預測模型的精度。

1 改進的SSA-KELM模型

1.1 小波分解

小波分解是采用非周期信號，通過應用基函數的不同尺度縮放去擬合被測信號的不同頻率，再通過平移基函數去擬合不同頻率分量在時間序列上位置的過程。小波變換可分為連續小波變換和離散小波變換兩大類。

選擇使用一維離散小波變換，離散小波基函數ψj，k(x)為

(1)

因此，信號f(x)的離散小波變換可表示為

(2)

1.2 麻雀搜索算法

麻雀搜索算法是一種新型的群智能優化算法，在2020年由Xue等[15]提出，主要是受麻雀的覓食和反哺食行為啟發，具有尋優能力強、收斂速度快的特點。

麻雀搜索算法將整個麻雀種群分為三類，即尋找食物的生產者，搶奪食物的加入者和發現危險的警戒者。生產者和加入者可以相互轉化，但各自在種群中的占比不會發生變化。

在模擬實驗中，需要使用虛擬麻雀進行食物的尋找，與其他尋優算法相同，麻雀搜索算法首先需要對麻雀種群與適應度值進行初始化，麻雀種群可初始化為如下形式，表達式為

(3)

式(3)中：n為麻雀的數量；d為要優化的變量的維度即獨立參數的數目；xn，d為第n只麻雀第d維度的值。

由此，總體麻雀適應度值表征形式為

(4)

式(4)中：f(x)為個體適應度值。適應度值較好的麻雀(即生產者)在搜索中會優先獲得食物并指引群體的覓食方向與范圍，與此同時，生產者會具有更大的覓食搜索范圍。

生產者在覓食過程中，位置不斷發生移動，而在遇到捕食者時，移動規則又會發生改變，即

(5)

而對加入者而言，在覓食過程中，一旦生產者找到了好的食物源，加入者必會知曉，并飛向它的附近搶食，同時，也有加入者會時刻監視生產者，隨時準備爭搶食物。由此加入者的位置更新規則為

(6)

總體而言，假設意識到危險的麻雀(即警戒者)占10%～20%。初始位置則隨機產生，規則為

(7)

式(7)中：λ為步長控制函數，是一個均值為0，方差為1的正態分布隨機數；fi為當前麻雀適應值；fg為全局最好適應值；fw為全局最差適應值；k為麻雀移動方向；xbest為全局最優位置；ε為最小常數，避免除數為零。當fi>fg時，警戒者位于種群邊緣，意識到危險后向中央安全區靠近；當fi=fg時，則是處于種群中央的麻雀意識到了危險，為躲避危險，則向其他麻雀身邊靠攏。

1.3 核極限學習機算法

傳統的單隱層神經網絡由三部分組成，分別是輸入層、隱含層和輸出層，輸入層神經元節點個數即輸入變量的個數，隱含層節點個數則需要人為給定，輸出層節點個數也就是輸出變量的個數。

在2006年，新加坡南洋理工大學的Huang等[16]在傳統的單隱層神經網絡的基礎上提出了一種新的前饋神經網絡學習算法，命名為極限學習機(extreme learning machine， ELM)，不同于傳統的基于梯度的前饋神經網絡算法，該方法隨機產生隱含層與輸入層之間的連接權值及隱含層神經元的閾值，訓練過程中只需要設置隱含神經元的個數便可獲得唯一最優解，極限學習機網絡結構如圖1所示。

圖1 極限學習機的網絡結構Fig.1 Network training model of ELM

在極限學習機中，假設有N個隨機樣本，設其為(Xi，ti)，其中，xi=[xi1，xi2，…，xin]T∈Rn，ti=[ti1，ti2，…，tim]T∈Rm，R為實數，則對于具有L個隱含層神經元的單隱層神經網絡，它第i個節點的輸出hi(x)可表示為

hi(x)=g(wi，bi，xi)=g(wi·xi+bi)

(8)

式(8)中：wi為輸入權重；bi為第i個隱含層神經元的閾值；wi·xi為wi和xi的內積；g(x)為一個任意區間無限可微的激活函數，激活函數可自行設置，常用的激活函數有sig、sin、hardlim等，但也有研究表明，激活函數既可以是非線性函數，也可以為不可微函數或不連續函數。

則隱藏層輸出矩陣為

H(x)=[h1(x)，h2(x)，…，hL(x)]

(9)

由此，輸出層可表示為

fL(x)=H(x)β

(10)

式(10)中：β=[β1，β2，…，βL]T為隱藏層與輸出層之間的輸出權重。

由式(8)～式(10)可知，極限學習機中需求解的有3個未知量：w、b、β。通過ELM的特殊性質來求解。ELM對單隱層前饋神經網絡的訓練主要分為如下兩個階段。

(1)隨機特征映射。即隨機產生隱含層的參數w和b，在傳統的反向傳播(back propagation，BP)神經網絡中，這兩個參數通過計算得來，而ELM的做法則大大提升了運算效率。

(2)線性參數求解。在確定了輸入權重w和隱含神經元閾值b之后，通過式(8)、式(9)可求得隱藏層的輸出矩陣H，進而通過最小化近似平方差的方法對β進行求解，目標函數如下：

min‖Hβ-T‖2，β∈RL×m

(11)

其中，期望矩陣為

T=[T1，T2，…，TN]T

(12)

輸出矩陣為

H=[h(x1)，h(x2)，…，h(xN)]T

(13)

其解為β*=H?T，其中，H?為矩陣H的Moore-Penrose廣義逆矩陣。

因為ELM中的輸入權重w和隱含神經元閾值b是隨機產生，算法效果不穩定，所以之后Huang等[17]為了算法的準確性和穩定性，又在算法中引入了核參數，使其代替ELM的隨機特征映射，形成核極限學習機算法。

通過正交投影和嶺回歸(ridge regression)理論，引入正則化系數C，則輸出權重可表示為

(14)

因此輸出函數

(15)

式(15)中：K(x，xi)為核函數。

1.4 模型建立

利用麻雀搜索算法對核極限學習機的兩項參數：核參數K及正則化系數C進行優化，得到SSA-KELM耦合滑坡預測模型，其實施步驟如下。

步驟1初始化種群。設置麻雀數量為20，隨機產生初始核參數K及正則化系數C，生成種群初始位置。

步驟2確定優化參數的取值范圍。根據多次實驗，確定核參數K為(-1010，1010)，正則化系數C為(-1010，1010)。

步驟3建立SSA-KELM耦合模型，計算麻雀個體適應度f(xi)，i=1，2，…，n，對適應度值進行排序，尋找出當前最好和最差的個體。適應度函數為

(16)

步驟4根據式(5)～式(7)更新麻雀位置。

步驟5獲取新的麻雀位置及個體適應度值，將本輪最優適應度值與之前的最優適應度值做比較，如果本輪更優，則更新全局最優適應度值Gbest與相關位數。

步驟6循環結束。當迭代次數大于500，則尋優過程結束。

步驟7得到KELM的最佳訓練參數，模型建立。

改進的SSA-KELM模型滑坡預測流程如圖2所示，算法結構如圖3所示。

圖2 改進的SSA-KELM模型滑坡位移預測流程圖Fig.2 The flow chart of landslide displacement prediction based on the improved SSA-KELM model

圖3 改進的SSA-KELM算法框架Fig.3 The framework of the improved SSA-KELM algorithm

2 模型精度評價

使用三項指標來評定模型精度，分別為均方根誤差(root mean square error，RMSE)、平均相對誤差絕對值(mean absolute percentage error，MAPE)和相關性系數(R)。RMSE和MAPE的值越小，預測效果越好；R越大，則預測效果越好。各精度評價指數的計算公式如下。

(1)均方根誤差。

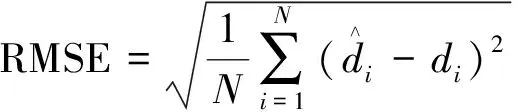
(17)

(2)相關性系數。

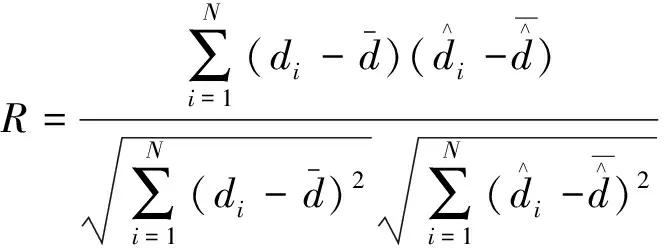
(18)

(3)平均相對誤差絕對值。

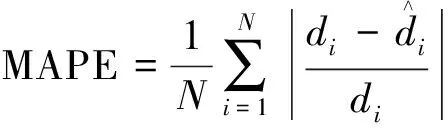
(19)

3 研究區概況

研究區滑坡位于金沙江中游阿海水電站左岸，距壩址約37 km，沿南北向分布，縱向長度約1.5 km，寬約600 m，滑坡體總方量約6 970×104m3，該滑坡體屬中厚層混合特大型堆積體，其前端有塌滑現象，地形呈圈椅狀，地貌特征明顯，為仍在活動的滑坡。從資料來看，造成滑坡的原因有以下三方面。

(1)堆積體原始岸坡前緣較陡，阿海水電站水庫體地下水位線抬升，部分巖(土)體處于飽水狀態，物理力學性質(如含水量、干重度、孔隙比等)發生了改變；堆積體前緣庫岸再造，局段出現崩塌、小滑坡，形成新的臨空面；水位變化產生動水壓力，受力狀態發生改變。

(2)2013年雨季降雨，大量的雨水集中下滲，下滲水流對堆積物的結構、物理力學性質產生了一定程度的惡化作用。

(3)人類活動(建房、修路、生產生活用水排放等)改變了堆積體地表形態，并惡化了穩定條件。

綜上，由于庫水浸泡和水位變化及降雨下滲，加之人類工程活動影響，打破了堆積體原有的平衡條件，導致大范圍產生滑移變形。

4 滑坡變形監測

該滑坡上布設有15個GPS監測點， GPS數據平時每隔3個月采集一次，雨季的7—9月每個月采集一次，合計每年6～7次。同時，該滑坡體還設有一個GPS自動監測站，進行24 h實時監測。該數據波動比較大，原因主要是測量間隔較短(實時監測)，但變形趨勢與附近人工監測點趨勢相吻合。GPS監測點布設狀況如圖4和圖5所示。

5 滑坡位移預測

考慮到GPS點監測時間的連貫性與監測數據的變化幅度大小，選用2013年1月—2018年底Ⅲ區的GPS滑坡監測數據作為實驗樣本，由監測點位移時間曲線(圖5)可知，選取滑坡變形時間最長、累計位移量最大且平均變形速率最快的XJ17監測點作為研究對象，選擇2013年1月—2018年1月的數據作為模型訓練集，2018年2月—2018年底的數據作為預測集。實驗在MATLAB2018b軟件中進行。

圖4 滑坡體及其周邊監測點布置圖Fig.4 Layout of monitoring points of the landslide and its surrounding bodies

5.1 數據預處理

(1)對GPS點XJ17進行線性插值，得到等間距的位移時間序列。

(2)使用db4小波變換，根據式(1)和式(2)將插值后的位移時間序列分解為趨勢項位移與周期項位移。

(3)對分解后的數據進行線性函數歸一化處理，統一映射到[-1，1]區間內。如此，既可提高函數尋優速度，也在一定程度上提高了求解的精度。歸一化公式為

(20)

圖5 GPS監測點位移-時間曲線Fig.5 Curves of cumulative displacement of GPS monitoring points vs time

5.2 趨勢項位移預測

趨勢項位移代表了多年以來滑坡變形的總體趨勢，是滑坡位移預測中最為關鍵的一項。采用改進的SSA-KELM算法對趨勢項位移進行預測，尋優得到的正則化系數C為1010，核參數K為-0.265 4，將預測結果反歸一化后與SVM進行對比，對比結果如圖6所示。

從精度對比表1中可知，SSA-KELM對趨勢項的預測結果更好。同時，算法的收斂曲線如圖7所示，可以看到，預測算法收斂速度很快。

圖6 不同模型趨勢項位移預測結果對比Fig.6 Comparison between predicted and measured trend displacement by different models

表1 不同模型趨勢項位移預測模型精度對比Table 1 Prediction performance comparison of trend displacement by different models

圖7 趨勢項位移預測模型收斂曲線Fig.7 Convergence curve of trend displacement prediction model

5.3 周期項位移預測

選取當月降雨量、雙月降雨量、滑坡當月位移增量、前兩月位移增量和前三月位移增量作為影響因子[18]對XJ17點進行對比分析，變化趨勢如圖8所示。

采用灰色關聯度法計算影響因子與周期項位移之間的關聯度，其關聯度如表2所示，關聯度均大于0.6，表明所選影響因子與周期項位移之間具有強相關性。

將影響因子和周期項位移訓練集中的數據作為模型輸入項，通過麻雀搜索算法尋優得到KELM的最優訓練參數C=-3.08×1010，K=1010，進而得到反歸一化后的預測結果，為檢驗該算法預測效果，引入支持向量機算法與模型預測效果進行對比，其對比曲線如圖9和表3所示。

圖8 周期項位移與影響因子關系Fig.8 Relationships between periodic displacement and influence factors

表2 周期項位移與影響因子關聯度Table 2 Degrees of gray correlation between the period term displacement and influence factors

圖9 不同模型周期項位移預測結果對比Fig.9 Comparison between predicted and measured periodic displacement by different models

在周期項位移預測結果中可以看到，雖然兩種預測模型的預測結果與實際值都有一定差距，但相比SVM，改進的SSA-KELM預測模型在各項評價參數上明顯更優，擬合效果更好，其算法收斂曲線如圖10所示，收斂速度較快。

同時，對該點進行多次預測實驗，算法尋優結果與位移預測結果均不變，說明算法具有很好的穩定性。

表3 不同模型周期項位移預測精度對比Table 3 Prediction performance comparison of periodic displacement by different models

圖10 周期項位移預測模型收斂曲線Fig.10 Convergence curve of periodic displacement prediction model

5.4 滑坡累計位移預測

將預測得到的周期項位移和趨勢項位移結果相加，得到的最終累計位移預測結果如圖11和表4所示。

使用同樣的方法對監測點XJ04進行預測，兩種方法的預測結果如圖12和表5所示。對XJ04和XJ17兩點的預測結果表明，相比SVM模型，改進的SSA-KELM模型對滑坡位移的整體預測精度更高，新模型具有較好的普適性。

圖11 XJ17的累計位移預測結果Fig.11 Cumulative displacement prediction values of XJ17

表4 累計位移預測精度對比表(XJ17)Table 4 Prediction performance comparison of cumulative displacement by different models(XJ17)

圖12 XJ04的累計位移預測結果Fig.12 Cumulative displacement prediction values of XJ04

表5 累計位移預測精度對比表(XJ04)Table 5 Prediction performance comparison of cumulative displacement by different models(XJ04)

6 結論

(1)提出了一種基于改進的SSA-KELM耦合算法的滑坡位移預測模型。通過使用麻雀搜索算法對核極限學習機的正則化系數與核參數進行尋優，只需設置麻雀數量和最大迭代次數兩項參數，便可取得位移預測結果，相比傳統的需要設置大量參數的SVM算法，該預測模型需要人為干預的參數更少。

(2)對XJ04和XJ17兩點的預測結果表明，改進的SSA-KELM算法相較于傳統的SVM算法預測精度更好，該算法具有較高的穩定性和較好的普適性，是一種準確有效的滑坡預測模型。

(3)由于獲取的GPS數據不可避免地存在人為誤差和系統誤差，同時獲取GPS數據的時間間隔不等，最終預測效果也必然受到影響。在條件允許的情況下，更多的GPS監測數據與相關影響因子(如地下水位、庫水位等)的加入將更有利于模型的訓練與預測。