高考中幾何概型的交會命題

何偉軍

(甘肅省定西市渭源縣第一中學)

幾何概型在高考中常與函數、不等式、線性規劃、定積分、平面向量、解析幾何等知識交會命題，命題的角度新穎、立意遠，考查的知識全面、綜合性強、能力要求較高，所以這類問題應當引起學生的高度重視.

1 幾何概型與函數零點、不等式交會

例1在區間[0，1]上任意取兩個實數a，b，則函數在區間[－1，1]上有且僅有一個零點的概率為_________.

解析

在區間[0，1]上任意取兩個實數a，b全部結果構成事件Ω＝{(a，b)|0≤a≤1，0≤b≤故f(x)在x∈[－1，1]上單調遞增.又因為函數上有且僅有一個零點，即有f(－1)f(1)＜0成立，即a－b)＞0，于是所求事件構成的平面區域為

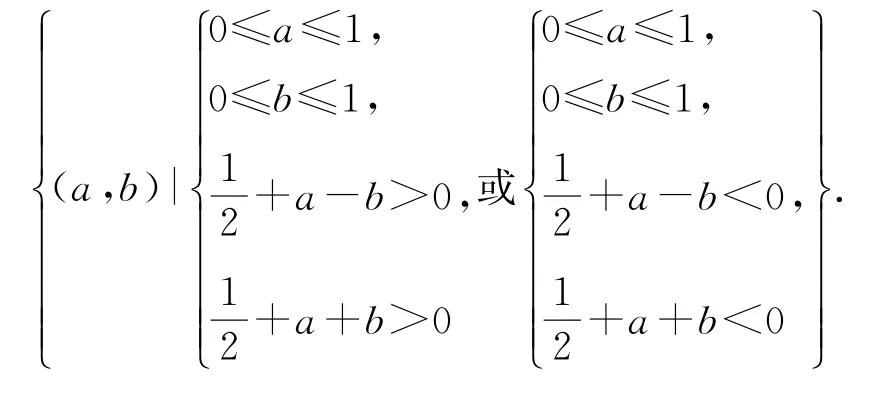
在平面直角坐標系aOb中畫出這兩個不等式組所表示的可行域，如圖1的陰影部分所示，因為正方形的面積為S＝1，陰影部分的面積為所以函數上有且僅有一個零點的概率為

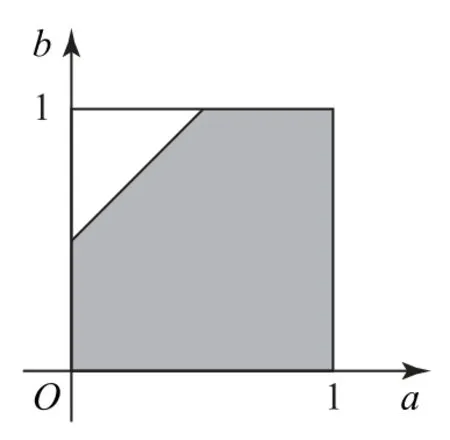
圖1

點評

本題將函數在給定區間上的零點與幾何概型交會在一起，綜合性強，解題時要注意基本事件和所求事件所構成的區域，用線性規劃的基礎知識解決.當基本事件受兩個連續變量控制時，一般要把兩個連續變量分別作為一個點的橫坐標和縱坐標，這樣基本事件就構成了平面上的一個區域，即可借助平面區域解決.

2 幾何概型與三角函數交會

例2已知函數f(x)＝sinx＋cosx，當x∈[0，π]時，f(x)≥1成立的概率為_________.

解析

點評

含單變量構成試驗結果的區域是區間的長度，實質是三角不等式的解集構成所求事件的區域長度.

3 幾何概型與定積分交會

例3如圖2所示，在邊長為e(e為自然對數的底數)的正方形中隨機撒一粒黃豆，則它落到陰影部分的概率為________.

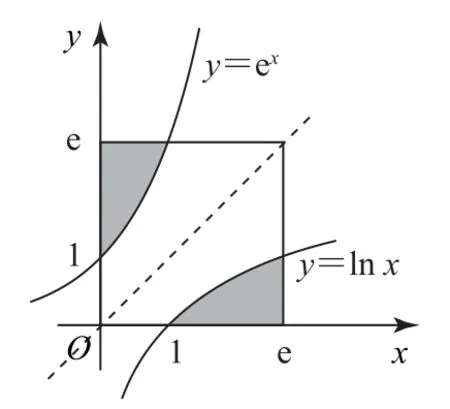
圖2

解析

由對數函數與指數函數的對稱性，得兩塊陰影部分的面積相同(如

圖2).S＝2(ex－ex)2，故落到陰影部分的概率為

點評

解答本題的關鍵是把題中所表示的幾何模型轉化為封閉圖形的面積，然后求解，注意我們常通過定積分來求曲邊多邊形的面積.

4 幾何概型與平面向量交會

例4已知向量a＝(－2，1)，b＝(x，y).

(1)若x，y分別表示將一枚質地均勻的正方體骰子(六個面的點數分別為1，2，3，4，5，6)先后拋擲兩次第一次、第二次出現的點數，求滿足a·b＝－1的概率;

(2)若x，y在連續區間[1，6]上取值，求滿足a·b＜0的概率.

解析

(1)將一枚質地均勻的正方體骰子先后拋擲兩次，所包含的基本事件的總數為6×6＝36個.由a·b＝－1，得2x－y＝1，所以滿足a·b＝－1的基本事件為(1，1)，(2，3)，(3，5)共3個.故滿足a·b＝－1的概率為

(2)若x，y在連續區間[1，6]上取值，則全部基本事件的結果為Ω＝{(x，y)|1≤x≤6，1≤y≤6}.滿足a·b＜0的基本事件的結果為A＝{(x，y)|1≤x≤6，1≤y≤6，－2x＋y＜0}，畫出圖形(如圖3).矩形的面積為S＝25，陰影部分的面積為4＝21，故滿足a·b＜0的概率為

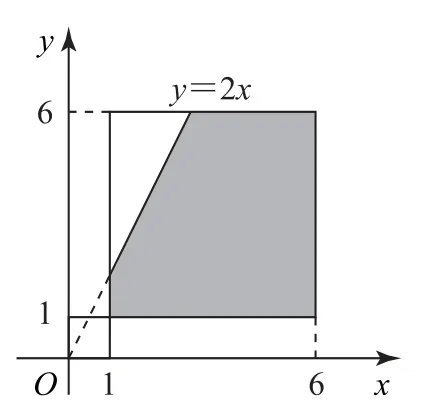
圖3

點評

第(1)問中先后拋擲兩次的點數對(x，y)為基本事件，只有有限個，而a·b＝－1的基本事件出現只有3個，是典型的古典概型.第(2)問中x，y在連續區間[1，6]上取值，可能出現的結果有無限多個，是幾何概型，明確事件所占整個區域是矩形，而滿足a·b＜0所占區域是梯形.由于變量取值的有限性和無限性，古典概型與幾何概型異同也顯而易見.

5 幾何概型與線性規劃交會

例5設不等式組表示的平面區域為D.在區域D內隨機取一個點，則此點到坐標原點的距離大于2的概率是( ).

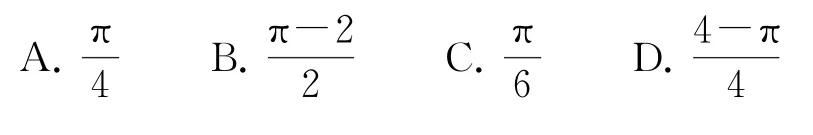
解析

設所求事件為A.如圖4所示，基本事件總數是邊長為2的正方形區域μ，滿足事件A的是陰影部分區域μA，故由幾何概型公式得P(A)＝故選D.

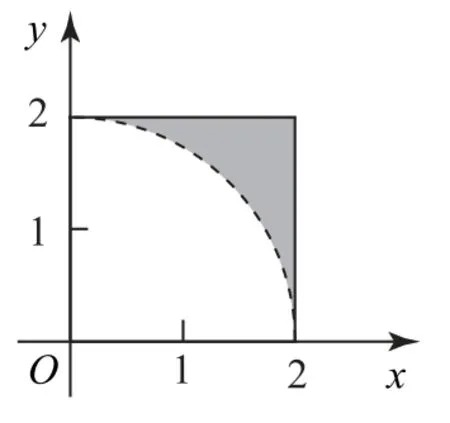
圖4

點評

本題所求的點落到陰影部分中，所以準確確定幾何空間的度量，應用公式進行計算是求解的關鍵.

6 幾何概型與直線、圓交會

例6在圓x2＋y2＝4上任取一點，該點到直線的距離d∈[0，1]的概率為_________.

解析

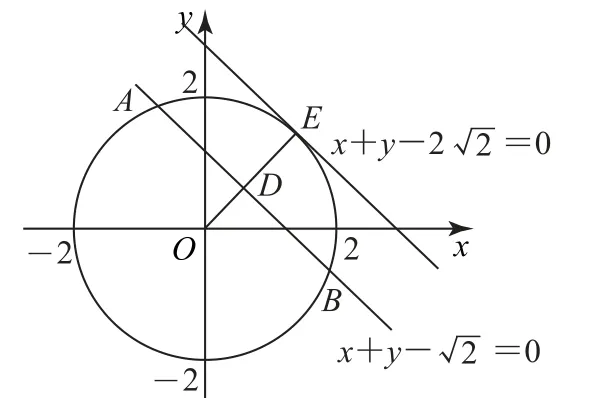
圖5

點評

將圓上哪些點到直線x＋y－2 2＝0的距離d∈[0，1]的問題，轉化為尋找與兩平行直線所夾圓弧，再求所夾圓弧對應的圓心角，是屬于與角度有關的幾何概型，且不可用線段的長度代替，但可以用圓心角所對應的弧長代替，這是兩種不同的度量方法.

7 幾何概型與解析幾何交會

例7已知直線與曲線恰有兩個不同的交點，記k的所有可能取值構成集合A;P(x，y)是橢圓上一動點，P1(x1，y1)與點P關于直線y＝x＋1對稱，記的所有可能取值構成集合B，若隨機地從集合A，B中分別抽出一個元素λ1，λ2，則λ1＞λ2的概率是________.

解析

方法1因為λ1∈A，λ2∈B，分別以λ1，λ2為橫坐標和縱坐標，點(λ1，λ2)構成一個平面區域Ω＝{(λ1，λ2)|0＜λ1＜1，－1＜λ2＜1}，該區域為圖6中面積為2的矩形;而所求事件A構成的區域A＝{(λ1，λ2)|0＜λ1＜1，－1＜λ2＜1，λ1＞λ2}是圖6中直角梯形(陰影部分)，故所求概率是

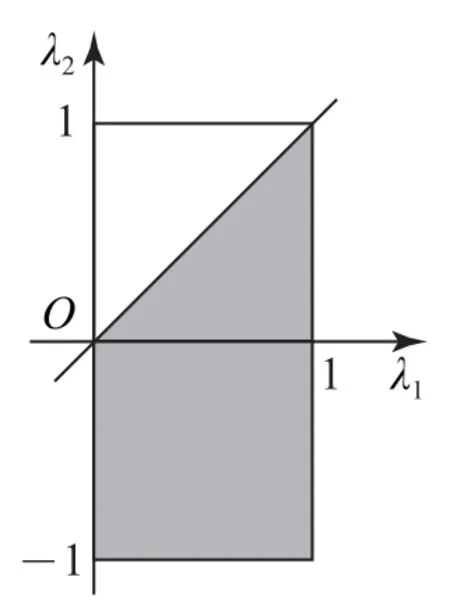
圖6

方法2當λ1∈A，λ2∈[－1，0]時，此事件發生的概率為此時必有λ1＞λ2;當λ1∈A，λ2∈(0，1]時，此事件發生的概率為此時λ1＞λ2與λ1≤λ2概率相等，各占于是滿足λ1＞λ2的概率為以上兩個事件為互斥，且[－1，0]與[0，1]的區間長度相等，故滿足λ1＞λ2的概率為

點評

本題將直線與曲線的交點、軸對稱圖形、二次方程根的分布、坐標的取值范圍、線性規劃、幾何概型等知識交會，綜合性強，解題時要注意將各個知識點分解轉化.

8 幾何概型與復數交會

例8設復數z＝(x－1)＋yi(x，y∈R)，若|z|≤1，則y≥x的概率為( ).

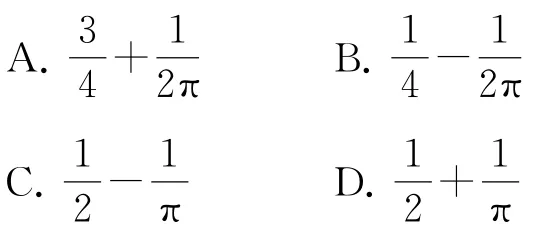
解析

z＝(x－1)＋yi，則1，即(x－1)2＋y2≤1.如圖7所示，易得A(1，1)，B(1，0)，則陰影面積為則y≥x的概率是故選B.

圖7

點評

由于復數與復平面內的向量一一對應，且復數模的幾何意義與平面區域密切相關，所以復數與幾何概型結合，令人耳目一新.

9 幾何概型與數學文化的交會

例9如圖8所示，來自古希臘數學家希波克拉底所研究的幾何圖形.此圖由三個半圓構成，三個半圓的直徑分別為Rt△ABC的斜邊BC，直角邊AB，AC.△ABC的三邊所圍成的區域記為Ⅰ，陰影部分記為Ⅱ，其余部分記為Ⅲ.在整個圖形中隨機取一點，此點取自Ⅰ，Ⅱ，Ⅲ的概率分別記為p1，p2，p3，則( ).

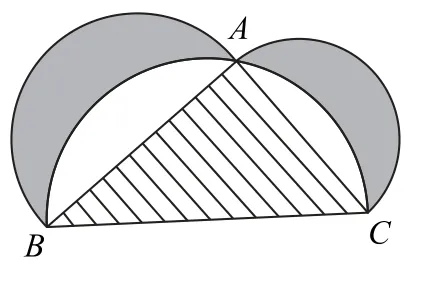
圖8

A.p1＝p2B.p1＝p3

C.p2＝p3D.p1＝p2＋p3

解析

方法1設Rt△ABC的內角A，B，C所對的邊分別為a，b，c，則區域Ⅰ的面積為△ABC的面積，即，區域Ⅱ的面積

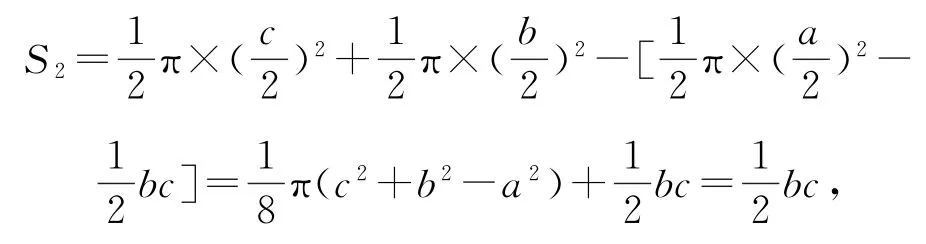
所以S1＝S2，由幾何概型的知識知p1＝p2，故選A.

方法2不妨設△ABC為等腰直角三角形，AB＝AC＝2，則，所以區域Ⅰ的面積為△ABC的面積，即區域Ⅱ的面積

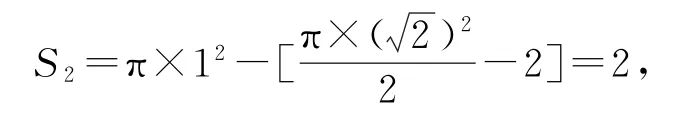
根據幾何概型的概率計算公式，得p1＝p2＝所以p1≠p3，p2≠p3，p1≠p2＋p3，故選A.點評

本題是幾何概型與數學文化交會的題，弄清區域的面積和面積的求法是關鍵，有一定的技巧性.此題文字較多，需要認真閱讀，并借助幾何圖形的特點，形成解決問題的思路.

總之，對于一個具體問題，首先要明確幾何概型的定義，關鍵在于能否將問題幾何化，能否應用幾何概型概率公式.要學會根據實際問題的具體情況，選取合適的參數，建立適當的坐標系，在此基礎上，將試驗的每一個結果一一對應于該坐標系中的點，使得全體結果構成一個可度量區域，即構造隨機事件對應的幾何圖形，利用圖形的幾何度量求隨機事件的概率.解幾何概型的試題，一般先求出試驗的基本事件構成的區域長度(面積或體積)，再求出所求事件構成的區域長度(面積或體積)，最后代入幾何概型的概率公式即可.