概率模塊章節小測

鄧超群 張國雯

(湖北省襄陽市第三中學)

(本試卷共22小題，滿分150分，考試用時120分鐘)

一、單選題(本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.)

2.某班有50名學生，其中有45名學生喜歡乒乓球或羽毛球，32名學生喜歡乒乓球，26名學生喜歡羽毛球，則該班既喜歡乒乓球又喜歡羽毛球的學生數占該班學生總數的比例是( ).

A.38% B.26% C.19% D.15%

3.已知隨機變量X的概率分布為其中a是常數，則P(0≤X＜2)的值等于( ).

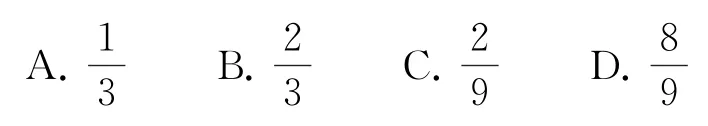
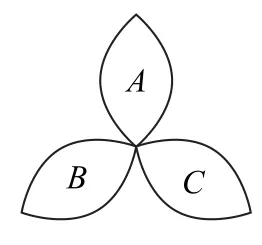
4.在荷花池中，有一只青蛙在成品字形的三片荷葉上跳來跳去(每次跳躍時，均從一葉跳到另一葉)，而且逆時針方向跳的概率是順時針方向跳的概率的兩倍，如圖所示.假設現在青蛙在荷葉A上，則跳三次之后停在荷葉A上的概率是( ).

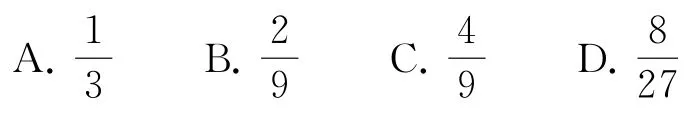
A.σ1＝σ2＞σ3

B.μ1＞μ3

C.μ1＝μ2

D.σ2＜σ3

6.饕餮紋是青銅器上常見的花紋之一，最早見于長江中下游地區的良渚文化陶器和玉器上，盛行于商代至西周早期.將青銅器中的饕餮紋的一部分畫到方格紙上，如圖所示，每個小方格的邊長為一個單位長度，有一點P從點A出發，每次向右或向下跳一個單位長度，且向右或向下跳是等可能的，那么點P經過3次跳動后恰好是沿著饕餮紋的路線到達點B的概率為( ).

7.七巧板，又稱七巧圖、智慧板，是中國古代勞動人民的發明，其歷史至少可以追溯到公元前一世紀，到了明代基本定型，于明、清兩代在民間廣泛流傳.某同學用邊長為4dm的正方形木板制作了一套七巧板，如圖所示，包括5個等腰直角三角形，1個正方形和1個平行四邊形.若該同學從5個三角形中任取出2個，則這2個三角形的面積之和不小于另外3個三角形面積之和的概率是( ).

8.為了提升學生身體素質，學校十分重視學生體育鍛煉.校籃球隊某位運動員在進行投籃練習.若他前一球投進則后一球投進的概率為若他前一球投不進則后一球投進的概率為若他第1球投進的概率為則他第2球投進的概率為( ).

二、多選題(本題共4小題，每小題5分，共20分.在每小題給出的選項中，有多項是符合題目要求的.全部選對的得5分，有選錯的得0分，部分選對的得2分.)

9.設0＜p＜1，已知隨機變量ξ的分布列如下表，則下列結論正確的是( ).

ξ 0 1 2 P p－p2 p2 1－p

10.甲罐中有5個紅球，2個白球和3個黑球，乙罐中有4個紅球，3個白球和3個黑球.先從甲罐中隨機取出1個球放入乙罐，分別以A1，A2和A3表示從甲罐取出的球是紅球、白球、黑球，再從乙罐中隨機取出1個球，以B表示從乙罐取出的球是紅球.則下列結論中正確的是( ).

11.2021年高考結束后小明與小華兩位同學計劃去老年公寓參加志愿者活動.小明在如圖的街道E處，小華在如圖的街道F處，老年公寓位于如圖的G處，則下列說法正確的是( ).

A.小華到老年公寓選擇的最短路徑條數為4條

B.小明到老年公寓選擇的最短路徑條數為35條

C.小明到老年公寓在選擇的最短路徑中，與到F處和小華會合一起到老年公寓的概率為

D.小明與小華到老年公寓在選擇的最短路徑中，兩人約定在老年公寓門口匯合，事件A:小明經過F;事件B:從F到老年公寓兩人的路徑沒有重疊部分(路口除外)，則

12.近年來中國進入一個鮮花消費的增長期，某農戶利用精準扶貧政策承包了一個新型溫室鮮花大棚，種植銷售紅玫瑰和白玫瑰.若這個大棚的紅玫瑰和白玫瑰的日銷量分別服從正態分布N(μ，302)和N(280，402)，則下列選項正確的是( )(附:若隨機變量X服從正態分布N(μ，σ2)，則P(μ－σ＜X＜μ＋σ)≈0.6826).

A.若紅玫瑰日銷售量范圍在(μ－30，280)的概率是0.6826，則紅玫瑰日銷售量的平均數約為250

B.白玫瑰日銷售量比紅玫瑰日銷售量更集中

C.紅玫瑰日銷售量比白玫瑰日銷售量更集中

D.白玫瑰日銷售量范圍在(280，320)的概率約為0.3413

三、填空題(本題共4小題，每小題5分，共20分.)

14.天氣預報說，在接下來的一個星期里，每天漲潮的概率為20%，設計一個符合要求的模擬試驗:利用計算機產生0～9之間取整數值的隨機數，用1，2表示漲潮，用其他數字表示不漲潮，這樣體現了漲潮的概率是20%，因為時間是一周，所以每7個隨機數作為一組，假設產生20組隨機數如下，則下個星期恰有2天漲潮的概率為_________.

16.甲、乙兩隊進行籃球比賽，采取七場四勝制(當一隊贏得四場勝利時，該隊獲勝，比賽結束).根據前期比賽成績，甲隊的主客場安排依次為“主主客客主客主”.設甲隊主場取勝的概率為0.6，客場取勝的概率為0.5，且各場比賽結果相互獨立，則甲隊以4∶1獲勝的概率是________.

四、解答題(本題共6小題，共計70分.解答應寫出文字說明、證明過程或演算步驟.)

17.(10分)如圖所示，周長為3cm圓形導軌上有三個等分點A，B，C，在點A處放一顆

珠子，珠子只能沿導軌順時針滾動.現投擲一枚質地均勻的骰子.每當擲出3的倍數時，珠子滾動2cm后停止，每當擲出不是3的倍數時，珠子滾動1cm后停止.

(1)求珠子恰好滾動一周后回到點A的概率;

(2)求珠子恰好滾動兩周后回到點A(中途不在點A停留)的概率.

18.(12分)計算機考試分理論考試與實際操作兩部分，每部分考試成績只記“合格”與“不合格”，兩部分考試都“合格”者，則計算機考試“合格”，并頒發合格證書.甲、乙、丙三人在理論考試中“合格”的概率依次為在實際操作考試中“合格”的概率依次為，所有考試是否合格相互之間沒有影響.

(1)假設甲、乙、丙三人同時進行理論與實際操作兩項考試，誰獲得合格證書的可能性最大?

(2)這三人進行理論與實際操作兩項考試后，求恰有兩人獲得合格證書的概率.19.(12分)某網站用“10分制”調查一社區人們的幸福度.現從調查人群中隨機抽取16名，莖葉圖記錄了他們的幸福度分數(以小數點前的一位數字為莖，小數點后的一位數字為葉).

(1)指出這組數據的眾數和中位數;

(2)若幸福度不低于9.2，稱該人的幸福度為“極幸福”.求從這16人中 隨機選取3人，至多有1人是“極幸福”的概率;

(3)以這16人的樣本數據來估計整個社區的總體數據，若從該社區(人數很多)任選3人，記ξ表示抽到“極幸福”的人數，求ξ的分布列及數學期望.

20.(12分)某種產品的質量以其質量指標值m衡量，并按照質量指標值m劃分等級如下表.

質量指標值m m＜85 85≤m＜105 m≥105等級 三等品 二等品 一等品

現在從某企業生產的這種產品中隨機抽取了200件作為樣本，檢驗其質量指標值m，得到的頻率分布直方圖如圖所示(每組只含最小值，不含最大值).

(1)求第75百分位數(精確到0.1);

(2)在樣本中，按照產品等級用比例分配的分層隨機抽樣的方法抽取8件產品，求這8件產品中，一等品的件數;

(3)將頻率視為概率，已知該企業的這種產品中每件一等品的利潤是10元，每件二等品和三等品的利潤都是6元，試估計該企業銷售600件這種產品所獲利潤.

21.(12分)直播帶貨是扶貧助農的一種新模式，這種模式是利用主流媒體的公信力，聚合銷售主播的力量助力打通農產品產銷鏈條，切實助力貧困地區農民脫貧增收.某貧困地區有統計數據顯示，2020年該地利用網絡直播形式銷售農產品的銷售主播年齡等級分布如圖甲所示，一周內使用直播銷售的頻率分布扇形圖如圖乙所示.若將銷售主播按照年齡分為“年輕人”(20歲～39歲)和“非年輕人”(19歲及以下或者40歲及以上)兩類，將一周內使用的次數為6次或6次以上的稱為“經常使用直播銷售用戶”，使用次數為5次或不足5次的稱為“不常使用直播銷售用戶”，則“經常使用直播銷售用戶”中有是“年輕人”.

(1)現對該地相關居民進行“經常使用網絡直播銷售與年齡關系”的調查，采用隨機抽樣的方法，抽取一個容量為200的樣本，請你根據圖表中的數據，完成2×2列聯表，并根據列聯表判斷是否有85%的把握認為經常使用網絡直播銷售與年齡有關;

年輕人 非年輕人 合計經常使用直播銷售用戶不常使用直播銷售用戶合計

(2)某投資公司在2021年年初準備將1000萬元投資到“銷售該地區農產品”的項目上，現有兩種銷售方案供選擇:

方案一:線下銷售.根據市場調研，利用傳統的線下銷售，到年底可能獲利30%，可能虧損15%，也可能不賠不賺，且這三種情況發生的概率分別為

方案二:線上直播銷售.根據市場調研，利用線上直播銷售，到年底可能獲利50%，可能虧損30%，也可能不賠不賺，且這三種情況發生的概率分別為

針對以上兩種銷售方案，請你從期望和方差的角度為投資公司選擇一個合理的方案，并說明理由.

參考數據:獨立性檢驗臨界值表如下.

P(K2≥k0)0.15 0.10 0.050 0.025 0.010 k0 2.072 2.706 3.841 5.024 6.635

22.(12分)甲、乙、丙、丁4名辯手進行辯論比賽，賽程如下面的框圖所示，其中編號為i的方框表示第i場比賽，方框中是進行該場比賽的兩名辯手，第i場比賽的勝者稱為“勝者i”，負者稱為“負者i”，第6場為決賽，獲勝的人是冠軍.已知甲每場比賽獲勝的概率均為而乙、丙、丁相互之間勝負的可能性相同.

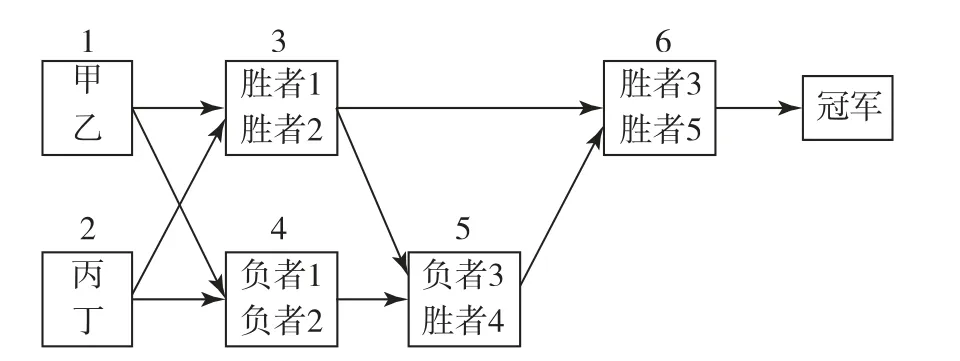
(1)求甲獲得冠軍的概率;

(2)求乙進入決賽，且乙與其決賽對手是第二次相遇的概率.