利用函數模型解決實際問題的策略

■徐春宇

函數模型可以清晰地刻畫實際問題中變量之間存在的聯系。下面從函數模型的應用、函數模型的選擇以及函數模型的構造等方面,幫助同學們學會合理地利用函數模型解決實際問題。

題型1:應用所給函數模型解決實際問題

此類題型的解題策略是先利用已知數據得出函數模型中的未知數,再把題目要求的數值代入完整的函數模型,即可求解。

例1某工廠產生的廢氣必須經過過濾后排放,規定排放時污染物的殘留含量不得超過原污染物總量的0.5%。已知在過濾過程中的污染物的殘留數量P(單位:mg/L)與過濾時間t(單位:h)之間的函數關系為P=P0·e-kt(k為常數,P0為原污染物總量)。若前4h廢氣中的污染物被過濾掉了80%,那么要使廢氣能夠按規定排放,還需要過濾nh,則正整數n的最小值為____。(參考數據:log52≈0.43)

解:由題目中已知信息可知,工廠前4h過濾了80%的廢氣污染物。已知污染物殘留數量與過濾時間的函數模型為P=P0·e-kt,所以前4h 還剩下(1-80%)=20%的未過濾污染物,所以(1-80%)P0=P0e-4k,可得0.2=e-4k,即-4k=ln0.2==ln(5-1)=-ln5,所以k=。

因為規定污染物的殘留含量不得超過原污染物總量的0.5%,所以0.5%P0≥P0e-kt,所以0.005≥e-kt。由k=,可得ln0.005≥,即-ln200≥,所以t≥=4log5200=8+12log52=8+12×0.43≈13.16,所以t≥13.16(t為正整數),可得t最小為14。故正整數n(過濾時間t)的最小值為14-4=10。

評析:此題提供了實際問題的函數模型以及部分數據,解題的關鍵是理解函數模型中變量的實際含義。

題型2:選擇函數模型解決實際問題

此類題型的解題策略是分析題目中數據的變化規律,結合不同函數模型的特征,從已知的函數模型中選擇最切合實際問題情境的函數模型。

例2某廠家為增加某種商品的銷售量,決定增加廣告投入費用,據市場調查,增加的銷售量x(單位:千件)與廣告投入費用H(x)(單位:萬元)滿足表1所示的數據(其中0≤x≤16)。

表1

為了描述增加的銷售量與投入廣告費用的關系,現有以下三種函數模型供選擇:H(x)=ax3+bx2+cx,H(x)=0.5x+a,H(x)=klogax+b(a,b,c∈R)。

(1)選出你認為最符合實際的函數模型,并求出相應的函數解析式。

(2)你認為銷售量增加達到多少時,才能使每千件的廣告費用最少?

解:(1)函數模型H(x)=0.5x+a是遞減函數,由已知數據對應遞增函數模型,可知函數模型H(x)=0.5x+a與已知數據不符合。函數模型H(x)=klogax+b在x=0處無意義,故也不符合題意。

對于函數模型H(x)=ax3+bx2+cx,它的遞增或遞減性由常數a,b和c決定,故是最合適的函數模型。

將表中的數據(1,0.452),(2,0.816),(4,1.328)代入H(x)=ax3+bx2+cx,化簡整理可得方程組由此解得故H(x)=0.002x3-0.05x2+0.5x(0≤x≤16)。

(2)設每千件的廣告費用為W,則關于W的函數模型為W(x)==0.002x2-0.05x+0.5。易得對稱軸方程x=12.5。當x=12.5 時,W(x)有最小值為W(12.5)=0.1875,所以當銷售量增加達到12.5 千件時,每千件的廣告費用最少。

評析:在選擇函數模型時,可以對比已知數據和函數模型的變化模式或變化趨勢。選擇的函數模型在某些特定點處要符合實際,如題中當x=0時函數所表示的意義。

題型3:構造函數模型解決實際問題

此類題型是較為復雜的函數應用題,通常會描述一個實際生活情境并提供實際問題中變量的具體數值或代表的未知數,要求挑選合適的變量,構建函數模型,并且利用構建好的函數模型進行答題。

例3如圖1,某單位在精準扶貧活動中,給一戶結對幫扶的貧困家庭贈送M、N兩種經濟作物的種子,并在三角形地塊OAB中劃出一部分來種植M種子,其余部分種植N種子。已知該地塊OA的長為70m,OB的長為50 m,邊OA上的高為40m。△OAB位于直線x=t(0≤t≤70)左側的地用來種植M種子,每平方米盈利元;右側的地用來種植N種子,每平方米盈利30元。記△OAB位于直線x=t(0≤t≤70)左側的圖形的面積為f(t)。

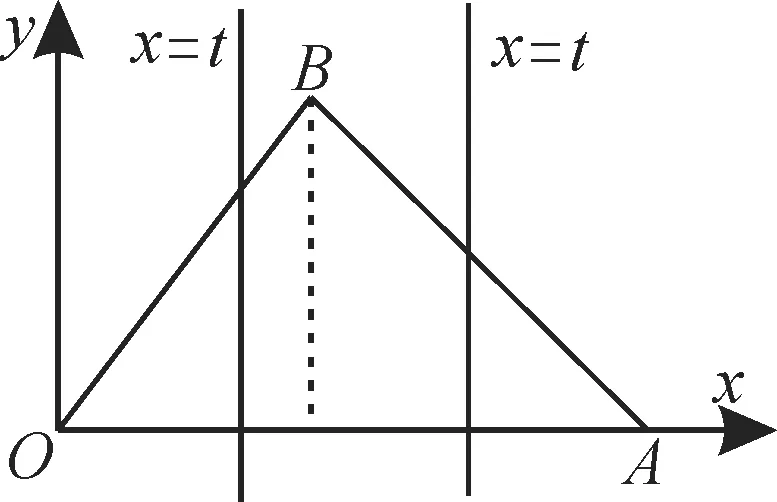
圖4

(1)求函數f(t)的解析式。

(2)設該農戶種植M、N兩種經濟作物的盈利總和為S元,求S的最大值。

解:(1)由題意可知點B(30,40),可得直線OB的方程為。同理可得直線AB的方程為y=70-x。

綜上所述,當t=5時,總盈利S取最大值42500元。

評析:本題主要考查分段函數模型在實際問題中的應用。對于第(2)問,當30＜t≤70時,如果把S=+42000展開,表達式比較復雜,最值不易求出,這時需要整體觀察+70t-1050的幾何意義,從而得出S＜42000＜42500,這樣就避免了復雜計算,使得解題過程簡單明了。