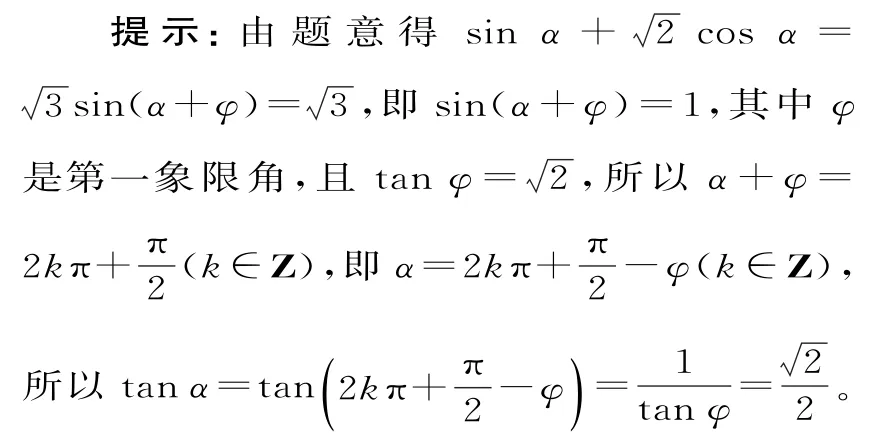探究輔助角公式中“φ”的確定與運用

■黃文青

在三角函數中,有一種常見而重要的題型,即化asinx+bcosx為一個角的三角函數形式,進而求原函數的周期、值域、單調區間等。這就要求同學們需要記憶和掌握輔助角公式。

一、輔助角公式中“φ”的確定方法

asinx+bcosx=(sinxcosφ+cosxsinφ)=,其中tanφ=,φ所在的象限由系數a,b的符號確定。一般地,由tanφ0=求出銳角φ0,若點(a,b)在第一象限,則取φ=φ0;若點(a,b)在第二象限,則取φ=π-φ0;若點(a,b)在第三象限,則取φ=π+φ0;若點(a,b)在第四象限,則取φ=-φ0。這樣處理輔助公式中的“φ”的值,既不容易出錯又簡單易學。

評析:在尋找角的過程中,一定要找“同一個角”的正弦值和余弦值。

練習1:函數f(x)=2sinxcosx-的最小正周期是____。

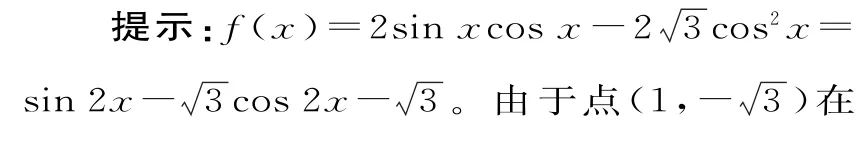
二、輔助角公式中“φ”的運用

對于輔助角“φ”,一方面要注重研究其來源,另一方面要把握輔助角與原生角的范圍關系,確定其大致范圍,可以更好地掌握和使用公式。

例2當x=θ時,函數f(x)=sinx-2cosx取得最大值,則cosθ=____。

評析:解答本題的關鍵是利用正弦函數的性質尋求輔助角與原生角的范圍關系。

練習2:已知,則tanα的值為____。