基于LMD-PCA和樣本熵的瓷支柱絕緣子故障診斷

邵鑫明，萬書亭，劉榮海，鄭 欣

(1.華北電力大學 機械工程系，保定 071003；2.華北電力大學 云南電網公司研究生工作站， 昆明 650217；3.云南電網有限責任公司 電力科學研究院， 昆明 650217)

瓷支柱絕緣子主要用于變電站隔離開關和母線的固定與絕緣。瓷支柱絕緣子的主要失效形式為斷裂，95%的斷裂位置在瓷柱與鑄鐵法蘭連接處，絕緣子一旦發生斷裂，會造成變電站、供電線路部分停電或全部停電，導致設備損害以及電量損失，嚴重影響社會的穩定和國民經濟建設[1-3]。造成瓷支柱絕緣子失效的原因有很多，主要分為制造缺陷，設計缺陷，安裝缺陷，調試缺陷以及運行環境等[4-5]。

現有的振動聲學瓷支柱絕緣子檢測法是通過絕緣子振動信號的頻譜來判斷絕緣子是否出現缺陷的[6]。李曉紅等[7]提出了對瓷支柱絕緣子振動信號進行 3 層小波包分解后對各節點能量進行提取分析的方法，利用支柱絕緣子故障發生前后能量的變化關系對有裂紋的絕緣子進行檢測。劉冠辰等[8]利用振動聲學的檢測方法，依據正常狀態下和缺陷狀態下的瓷支柱絕緣子擁有不同的固有頻率的原理，將固有頻率的差異作為故障判別的依據。

筆者通過振動聲學采集裝置采集絕緣子底部法蘭得到聲振信號，引入樣本熵作為瓷支柱絕緣子故障診斷的特征。首先采用局域均值分解方法(LMD)[9-10]將振動信號分解，得到若干PF(乘積函數)分量，再用主成分分析方法(Principal Components Analysis，PCA)[11]獲取主PF分量。然后選取主PF分量求其樣本熵[12]作為特征值，構造相應特征向量并輸入支持向量機分類器[13]中進行故障識別，提高瓷支柱絕緣子故障特征的識別效率。

1 LMD方法原理

LMD是一種信號分解的方法，與EMD(經驗模態分解)相比LMD具有更輕的端點效應且在處理分析結果時受端點效應影響較小，在形成包絡線時可以避免過包絡與欠包絡的現象[14-15]，對于任意信號x(t)，其分解過程如下。

(1) 找出原始信號x(t)所有局部極值點，并求出兩個相鄰極值點的平均值和包絡估計值。

mi=(ni+ni+1)/2

(1)

ai=|ni-ni+1|/2

(2)

式中:ni和ni+1為相鄰的兩個極值;mi為兩個相鄰極值點的平均值;ai為兩個相鄰極值點的包絡估計值。通過滑動平均的方法得到局部均值函數m11(t)和包絡估計函數a11(t)。

(2) 原始信號x(t)分離去除局部均值函數m11(t)，得到新的函數h11(t)。

h11(t)=x(t)-m11(t)

(3)

用h11(t)除以包絡估計函數a11(t)，對h11(t)進行解調，得到解調函數sn(t)。

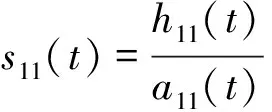
(4)

(3) 理想情況下，s11(t)是一個純調頻信號，但實際中并不是所有的s11(t)都滿足條件，為此將s11(t)進行迭代，迭代終止條件滿足a1n(t)=1，此時s1n(t)為一個純調頻信號。 當s1n(t)是純調頻信號時，得到第一個PF分量：

PF1(t)=a1(t)s1n(t)

(5)

式中:a1(t)為PF分量的包絡信號，s1n(t)為PF分量的純調頻信號。

(4)uk是PF(t)通過迭代分解k次分離得到的一個單調函數，此時x(t)可以由k個PF分量與uk之和構成

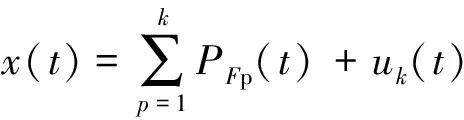
(6)

2 提取故障特征

2.1 PCA方法原理

主成分分析法(PCA)[16]利用降維的思想，幫助分類模型減少輸入向量，降低分類模型的復雜度。其分析步驟如下所述。

(1) 設P維隨機向量X=[x1,x2,x3,…,xn]共有n個樣本，則其轉置矩陣XT=[x1,x2,x3,…,xn]T。

(2) 對XT的每一行進行零均化處理，并求出X的協方差矩陣

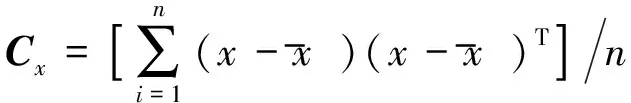
(7)

(3) 通過特征方程計算特征值與特征向量

|λIm-R|=0

(8)

式中：λ為特征值;R為相關系數矩陣。

經計算得到特征值λ1,λ2,…,λm與特征向量γ1，γ2，…，γm。

(4) 定義各特征值的貢獻率Cr和累計貢獻率Ct，計算公式為

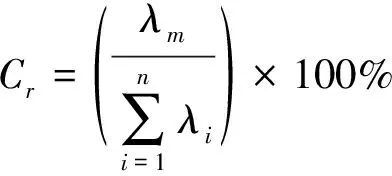
(9)

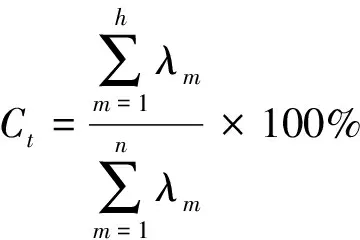
(10)

式中:m=1,2,…,h,…,n，其中h代表前h個特征值,當累計貢獻率Ct(h)≥85%時,將前h個特征向量γ1，γ2，…，γm構成的Rh(Rh=[γ1，γ2，…，γh])，作為降維后低維投影空間的矩陣。

2.2 樣本熵

對于由N個數據組成的時間序列x(n)={x(1),x(2),…,x(N)}，其樣本熵的計算步驟[17-18]如下。

(1) 按照序號組成一組維數為m的向量序列X(i)。

X(i)=[x(i),x(i+1),…,x(i+m-1)]

i=1,2,…,N-m+1

(11)

(2) 定義矢量x(i)與x(j)之間的距離d(i,j)。j=1,2,…,N-m(i≠j)

d(i,j)=|x(i+k)-x(j+k)|

(12)

式中:(k=0,1,…,m-1),求得(k=0,1,…,m-1)時d(i,j)的最大值。

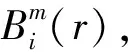
(13)

式中：i=1, 2, …,N-m+1,j≠i。

(14)

(5) 增加維數至m+1，重復步驟(1)～(4),可以得到Bm+1(r)。

(6) 若N取有限值，那么此序列長度為N時的樣本熵由以上理論可得:

(15)

3 現場試驗

3.1 瓷支柱絕緣子振動信號采集

以云南省某變電站110 kV在役瓷支柱絕緣子為研究對象。采用瓷支柱絕緣子帶電探傷儀(SCT)振動聲學檢測裝置，采集瓷支柱絕緣子的振動信號(見圖1)。該儀器以48 kHz的采樣頻率采集16 384點，并將采集到的振動信號以音頻格式儲存。經試驗研究表明，該儀器的兩個探頭抵在瓷支柱絕緣子的下法蘭上，能夠更好地獲取由激振器與法蘭面產生的振動信號。

圖1 瓷支柱絕緣子振動聲學檢測現場

瓷支柱絕緣子常出現裂紋的位置為其上法蘭和下法蘭處，其典型的振動信號如圖2所示。

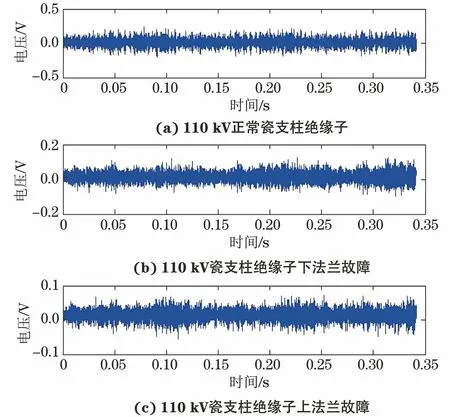
圖2 典型的瓷支柱絕緣子振動信號

從圖2原始信號時域內觀察瓷支柱絕緣子的3種狀態。振動信號雖然有一定的差異，但沒有明顯的規律，無法作為故障診斷的依據。瓷支柱絕緣子功率密度圖譜如圖3所示，通過查看瓷支柱絕緣子功率密度圖譜的范圍可以初步判斷絕緣子的故障狀態。

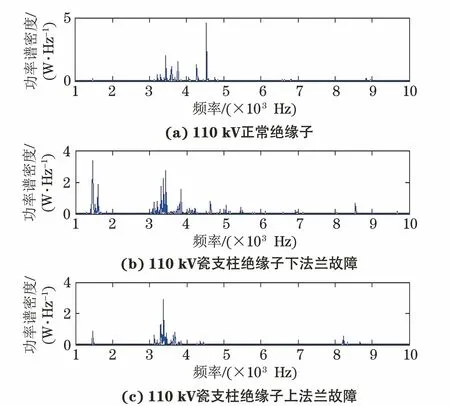
圖3 瓷支柱絕緣子功率密度圖譜

但此方法的缺點是需逐個檢測絕緣子小樣本，且頻率范圍的波動會影響對檢測結果的判斷，不適用于變電站眾多數量瓷支柱絕緣子的檢測。

從采集到的數據中選取20組正常狀態的瓷支柱絕緣子振動信號、20組上法蘭故障明顯的瓷支柱絕緣子振動信號、20組下法蘭故障明顯的瓷支柱絕緣子的振動信號，共得到60組數據，用以驗證文章提出的方法。

3.2 特征參數提取

受篇幅所限，以某一組下法蘭故障為例，對采集的信號進行LMD分解，其分解結果如圖4所示。

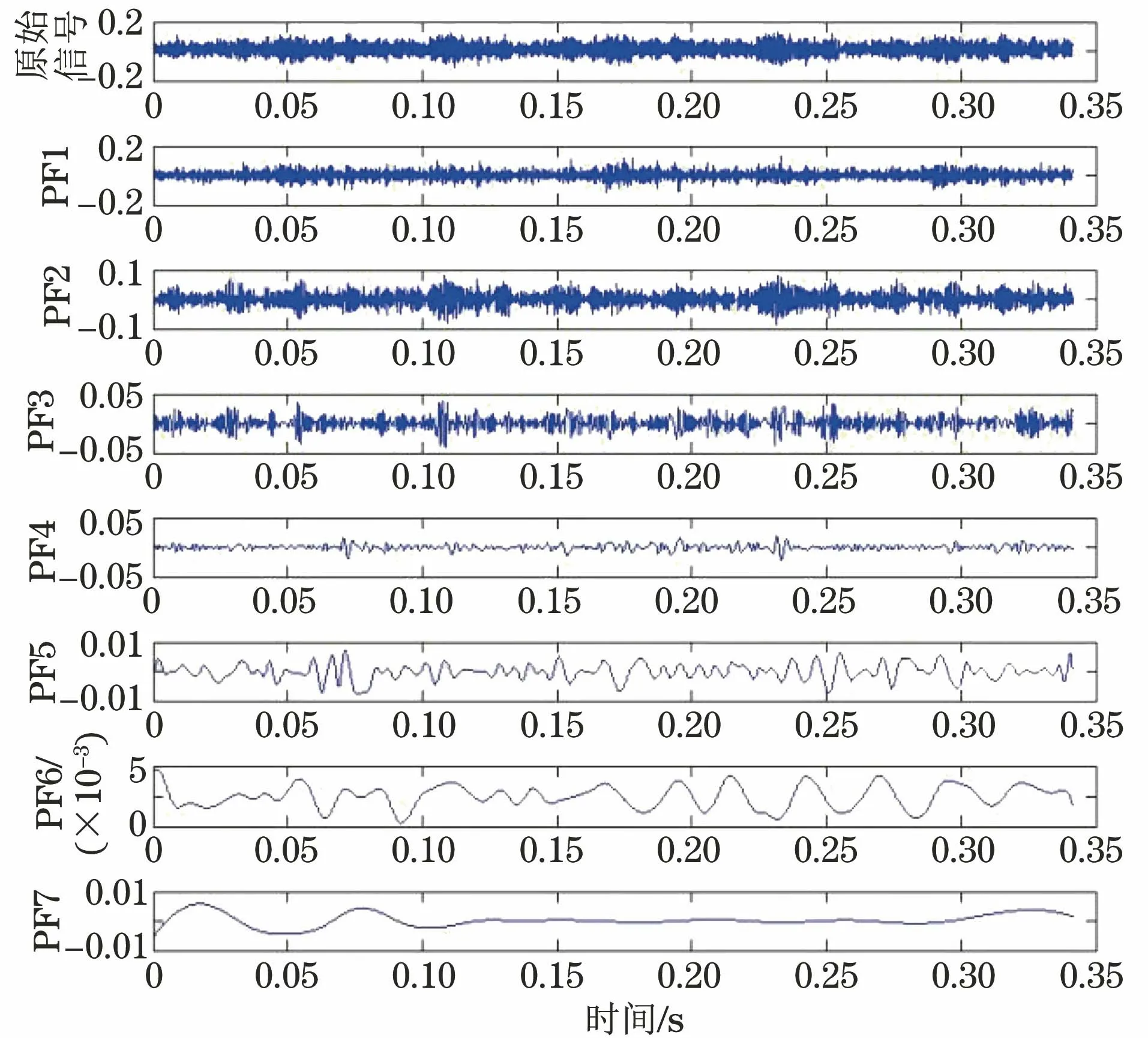
圖4 下法蘭故障信號LMD分解結果

由圖4可知，下法蘭故障信號經LMD分解得到7個PF分量。采集信號60組，共420個PF分量(見表1)。為了降低數據維度提高學習速度，且使信息損失減小，利用主成分分析獲取主PF分量，并求其樣本熵。

表1 采集信號LMD分解后的PF分量

由計算得特征值λ。λ=[2.978 7, 1.928 4, 0.929 7, 0.432 0， 0.387 5, 0.211 9,0.131 8]，再求各特征值的貢獻率及累計貢獻率，其結果如表2所示。

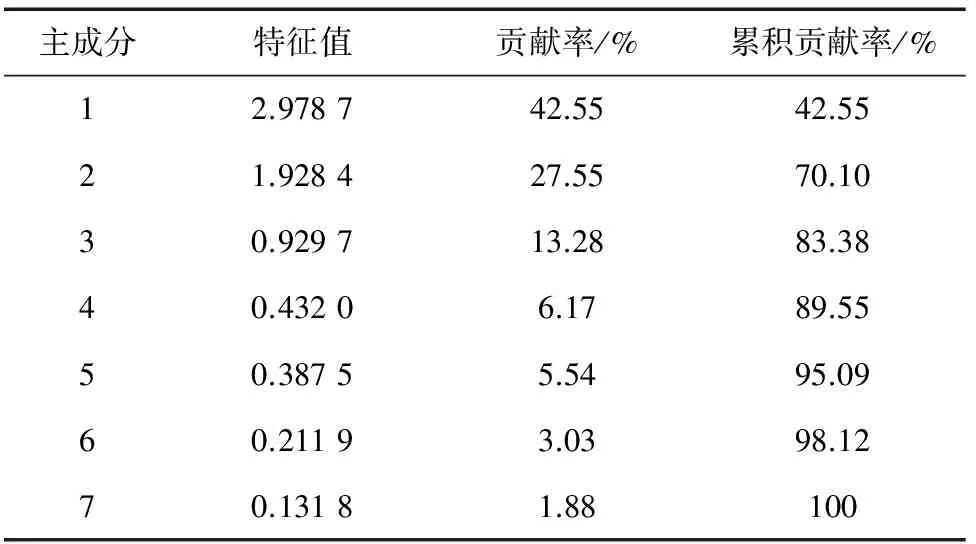
表2 各特征值貢獻率及累計貢獻率

本次分析選擇累計貢獻率不小于85%,故用作故障診斷的PF分量只保留前4個特征向量即可滿足要求。

分別計算不同狀態下PF分量的樣本熵，經過多次計算可得，當m=1,r=0.4(m為嵌入維數，r為相似容量)時前4個樣本熵的區分度較高。取PCA得到的前4個主PF分量求其樣本熵，結果如表3所示。

表3 瓷支柱絕緣子前4個主PF分量的樣本熵

對不同故障類型的樣本熵進行均值化處理得到的樣本熵均值如圖5所示，由于其樣本熵均值具有明顯的差異性，因此可以將樣本熵作為特征量用于后續的故障識別。

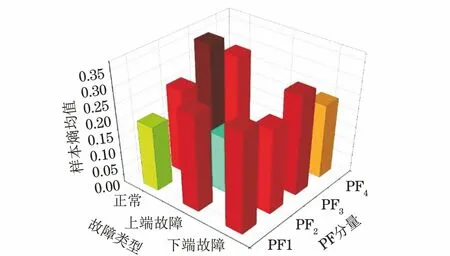
圖5 主PF分量的樣本熵均值柱狀圖

3.3 模式識別

瓷支柱絕緣子采集的信號樣本有限，屬于小樣本。支持向量機在解決小樣本時與其他模式識別方法相比更具有優勢[19-20]。從3種故障類型中，每種類型選15組數據，共45組數據作為訓練樣本；剩余15組數據作為測試樣本。支持向量機(SVM)是一個二分類器，其在3種狀態下，構造3個SVM，形成3組二分類器。此SVM選用的核函數為RBF(徑向基函數)，將測試數據導入樣本訓練得到的模型中進行計算，得到分類結果。類別標簽1，2，3分別代表瓷支柱絕緣子的3種狀態，測試集共15組，每種狀態5組，瓷支柱絕緣子分類結果如圖6所示。

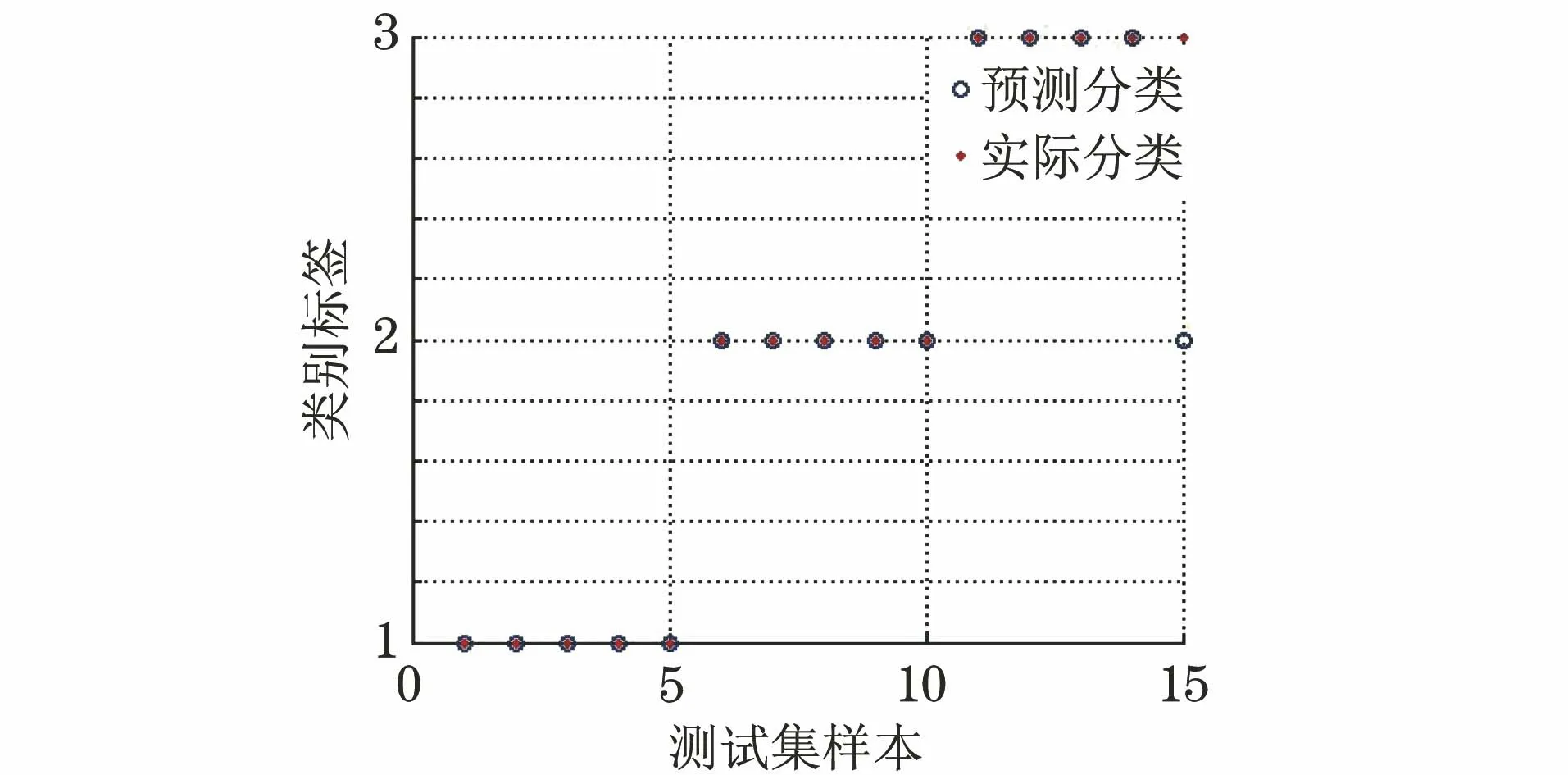
圖6 實際分類與預測分類對比

為驗證PCA方法提取主PF分量并求其樣本熵作為特征向量對識別結果的影響。分別在未用主PF分量且未用樣本熵(PF)；未用主PF量且使用樣本熵(PF-SampEn)；使用主PF分量且未用樣本熵(Main-PF)；使用主PF分量且使用樣本熵(Main-PF-SampEn)等4種狀態下，求其特征參數作為故障識別的特征向量，不同特征提取方法的識別率和分類時間如表4所示。

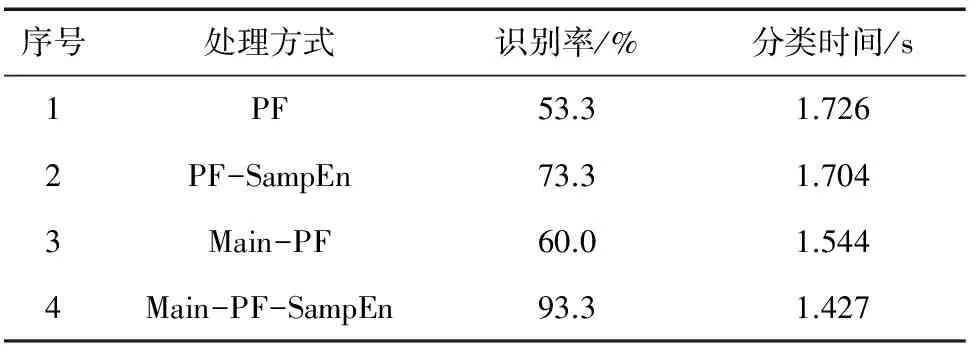
表4 不同特征提取方法的識別率和分類時間

由表4可知，在未使用PCA降維得到主PF分量的情況下，使用樣本熵處理的特征參數具有更高的正確識別率。這是因為樣本熵組成的特征參數差異性明顯，具有良好的特征提取性，故具備較高的狀態識別率；在都使用樣本熵處理特征參數的前提下，使用PCA降維得到的主PF分量作為特征參數，在識別率未降低的情況下具有更快的分類速度、識別精度和識別準確率。

4 結論

(1) 將LMD-PCA與樣本熵相結合的方法運用在瓷支柱絕緣子振動信號分析中，能夠有效提取瓷支柱絕緣子不同故障下的特征向量，通過SVM可以快速準確地識別絕緣子的故障類型。

(2) 對比不同的特征處理方法，發現在瓷支柱絕緣子振動信號分析中Main-PF-SampEn能夠為瓷支柱絕緣子故障分類識別提供低冗雜度的特征向量，提高了識別精度和識別效率。

(3) 使用PCA方法進行分析時，參數累計貢獻率的選擇很大程度上依賴于使用者的經驗以及信號的特點，因此，需要進一步研究參數選取的方法，增強該方法的適用性。