湍流槽道流并行直接求解方法

習令楚, 謝嘉斌, 包 蕓

(中山大學 航空航天學院， 廣州 510275)

在流體力學的湍流研究中，壁湍流是一個重要的問題，其在理論研究和工業應用方面都具有關鍵意義，引起了人們極大的興趣. 在壁湍流的問題當中，槽道流由于具有簡單的幾何模型和邊界條件，被視為一種非常有效的研究模型.

槽道湍流的實驗研究與數值模擬研究成果非常豐富. 直接數值模擬被認為是能夠得到最準確數據的數值模擬方法. 1987年，Kim等[1]通過直接數值模擬的方式計算了Reτ≈180的槽道流，并將計算的結果與早前Eckemlmann等[2]的結果進行了對比. 不過按照湍流研究的慣例，通常認為槽道流的內區為0.1個半槽道高度，而外區要大于50個壁面單位，Reτ必須足夠高才會在存在內區與外區的交錯段[3]. 同時Smits等[4]提出當Reτ達到103時湍流研究的結果接近工業上所需要的雷諾數，研究具有實際應用價值. Monty等[5]進行了最大Re=2 000的槽道湍流實驗, 為Hoyas等[6]計算的Reτ=2000和Alamo等[7]計算的Reτ=1 000的結果提供實驗驗證數據. Schultz等[8]進行了1 000≤Reτ≤6 000的槽道流實驗，主要的工作是測出不同雷諾數下的統計量，并且將新的數據與之前的DNS或者實驗的數據進行對比. 在數值模擬方面，Lozano等[9]計算了Reτ=4 200的槽道流，研究計算區域對數值模擬的影響，結論為計算區域(2πh×πh)在靠近壁面區域所得到的結果足夠準確. Lee等[10]計算了Reτ=5 200的湍流槽道流，并且對之前的DNS與實驗的結果進行了驗證與總結. 上面的計算均采用譜方法進行. Bernardini等[11]用二階有限差分法計算了Reτ=4 000的湍流槽道流，對他人的計算結果進行了驗證. 除了Bernadini等人采用二階有限差分法之外，Vela-Martin等[12]利用GPU對湍流槽道流開展計算，采用的方法為二階有限差分法，計算的雷諾數達到Reτ=5300；Yamamoto等人[13]采用高階精度的有限差分法，計算了Reτ=8 000的槽道流，但是由于計算的網格分辨率不夠高，在速度脈動的計算上面與目前所認可的規律相比相差較大，目前對這組數據仍然存疑. 目前最大雷諾數的槽道流算例是Hoyas等人[14]計算的雷諾數達到Reτ=10 000的槽道流，這組數據計算區域較小(2πh×πh)，目的是為了得到槽道流湍流的單點統計規律.

減阻控制是湍流槽道流的研究熱點和重點之一，實驗與數值模擬都進行了大量的研究. 湍流減阻具有代表性的工作包括Quadrio等[15]采用的壁面展向振動的方式、Luchini等[16]通過壁面溝槽限制了流向渦的展向流動以及Maden等[17]通過等離子體激勵器控制的方式減小了槽道湍流的阻力等研究.

隨著超級計算機性能與并行技術的提高，高Re數的槽道流DNS計算成為可能. 本文結合所在課題組基于湍流熱對流所建立的并行直接求解方法(PDM-DNS)，將較高效的并行求解方法引入湍流槽道流計算當中，實現較高效并行的湍流槽道流DNS模擬計算. 由于本文采用的計算方法是有限差分法，結合浸沒邊界法等計算技術，方便處理復雜的邊界條件，較容易將槽道流的計算研究擴展到湍流流動控制等計算研究領域.

1 槽道流的計算方法

由于計算規模巨大，高Re數湍流槽道流的DNS模擬往往需要使用高效并行計算技術并依托超級計算機進行. 湍流槽道流的計算結果數據可以為壁湍流理論研究以及湍流流動控制等研究提供基礎依據.

1.1 控制方程與其求解

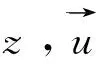
不可壓流動的控制方程為

(1)

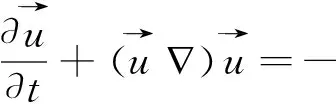
(2)

槽道流計算中，速度與壓力在流向與展向方向采用周期邊界條件, 上下壁面邊界條件為速度無滑移和零壓力梯度. 計算網格在流向與展向方向采用等距網格，垂直壁面方向采用壁面附近加密的非等距網格. 空間采用二階精度中心差分格式，時間采用二階精度的Runge-Kutta法進行計算. 本文采用的計算步驟為投影法.

實際的槽道流是由壓力驅動引起的流動. 本文采用定流量計算(CFR,Constant Flow Rate)，定流量指設定系統的流量恒定，系統的總流量不發生改變[18]. 控制流量的方法為在每個計算的單元內引入外加力Fx與Fy. 設初始的流量為Q0,計算n+1時刻的流量為Qn+1，所以有

(3)

對于流向與展向的速度u和v，通過引入外加力F修正以保證流量恒定.

1.2 直接并行求解方法與并行效率

對于槽道流的DNS計算來說，當Re數增大就需要提高計算網格精度，所以采用高效的并行計算在高Re數湍流槽道流的DNS模擬中是不可缺少的.

課題組在之前為解決極高Ra數湍流熱對流的DNS數值模擬，建立了直接并行求解方法PDM-DNS(Parallel Direct Method of Direct Numerical Simulation)[19]，Direct Method指的是直接求解法，在求解的過程對于壓力項的求解沒有采用迭代的方式而是直接求解壓力泊松方程得到壓力. 將這一計算方法引入到槽道流的計算中來，初步實現具有較高并行效率的湍流槽道流DNS模擬并行計算. PDM-DNS方法的計算特點是，采用OpenMP和MPI混編并行，可在“天河二號”超級計算機上運行. 其中關鍵技術是壓力泊松方程的高效并行求解，采用FFT解耦和PDD三對角方程并行求解技術.

表1給出了在“天河二號”超級計算機上進行槽道流DNS計算并行效率測試結果. 計算網格采用512×512×512，共1.34×109網格計算自由度. 采用PDM-DNS方法分別在超級計算機上應用1～8個計算節點，即32～256計算核進行計算，所有計算都能達到95%以上的并行效率，并且具有很好的并行效率的線性延展性. 因此，PDM-DNS方法可以給湍流槽道流DNS模擬提供較為高效的并行計算，使高Re數湍流槽道流的模擬得以實現并獲得大量有效的數據.

表1 在nx×ny×nz=512×512×512的網格下并行相關參數

1.3 湍流的生成方法

槽道流以層流泊肅葉流動作為初場，通過添加速度擾動使其發展成為湍流槽道流. 擾動大小幅值為初始速度大小的10%. 在外加擾動的作用之下，流動逐漸從層流向湍流進行轉變.

圖1給出了槽道流壁面摩擦系數隨時間的變化過程. 在不斷添加人為的擾動速度影響下，槽道壁面的摩擦系數隨著時間發生變化. 在無量綱時間T<20的時候，壁面摩擦系數幾乎是不變的；在20≤T≤35的階段，壁面的摩擦系數會出現一個突增的情況；在T>35之后，壁面摩擦系數發展到另一個較大的數值并趨于平穩，此時流動發展進入湍流狀態. 在流動發展到湍流狀態之后撤去人為的速度擾動，槽道流動不會回到層流流動而是穩定在湍流流動狀態，繼續計算最終得到充分發展的湍流槽道流，在此基礎上可得到湍流槽道流的研究數據.

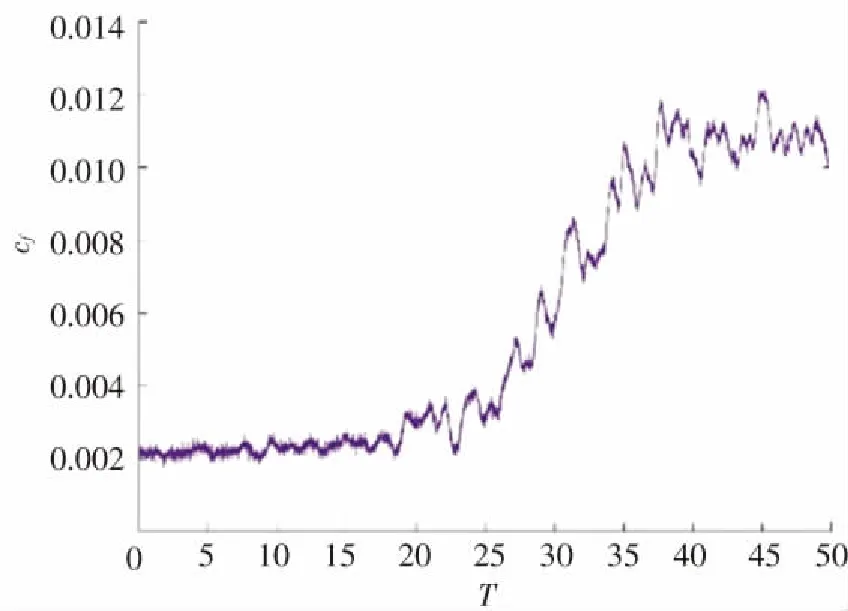
圖1 壁面摩擦系數隨著時間的變化

2 湍流槽道流DNS模擬結果與討論

設定半槽道的寬度為h，為了驗證程序的準確性，本文分別計算了Reτ≈180、550、1000、2 000時的4個算例，并且與相關的數值模擬進行對比. 計算算例的主要參數具體如表2所示.

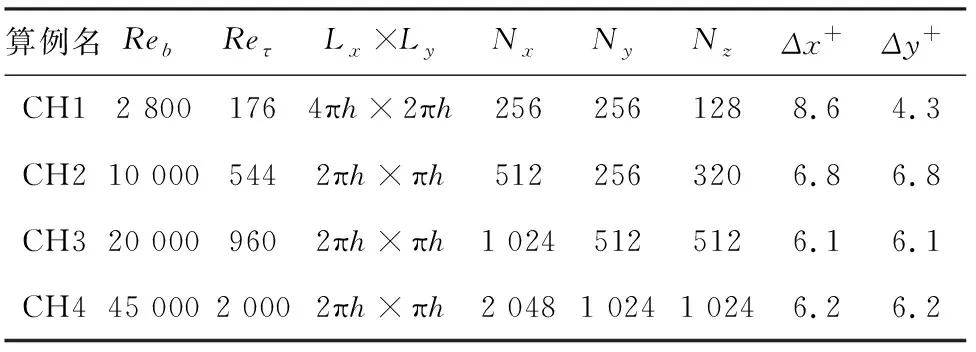
表2 槽道流算例的主要參數

對于網格精度，x方向控制在10個壁面單位以內，y方向控制7個壁面單位以內. 根據Jimenez等[9]的研究成果，計算區域取2πh×πh中等范圍，可以保證槽道流內區的計算具有足夠的準確性. 本文所采用的對比數據是Lee[10]的DNS計算結果，他們的結果可靠性得到世界的認可.

2.1 平均速度

在壁湍流的理論當中，一般認為在流動的內區到外區的平均流向速度是符合對數律的. 對數律的公式可以寫為

(4)

其中，κ指卡門系數. 在不同組的實驗當中所測出來的κ值也有些許差異，Osterlund[20]測出κ=0.38，Monty[5]測出κ=0.37，Nagib[21]測出κ=0.39. 由此可以認為κ在0.38附近，本文選取κ=0.38.

圖2給出了本文4個算例的平均速度剖面線，并給出相應的Lee[10]的DNS計算結果. 從圖2可以看出,CH1的結果在對數段相比其它的結果略高，原因是在Reτ≈180下，當z+≈50時，z/δ≈0.28，當z+≈30時，z/δ≈0.17，所以在槽道流當中并不存在交錯段(z+>50,z/δ<0.1)，但是存在對數段(z+>30,z/δ<0.3). 在Reτ≈550 時，在z+=50下，z/δ≈0.09，所以在槽道流當中既存在交錯段(z+>50,z/δ<0.1)，也存在對數段(z+>30,z/δ<0.3). 同樣現象在Lee的數據當中也有所體現. 在CH2～CH4的結果中都存在基本一致的對數段，且與Lee的結果相比較為接近，表明計算結果基本合理.

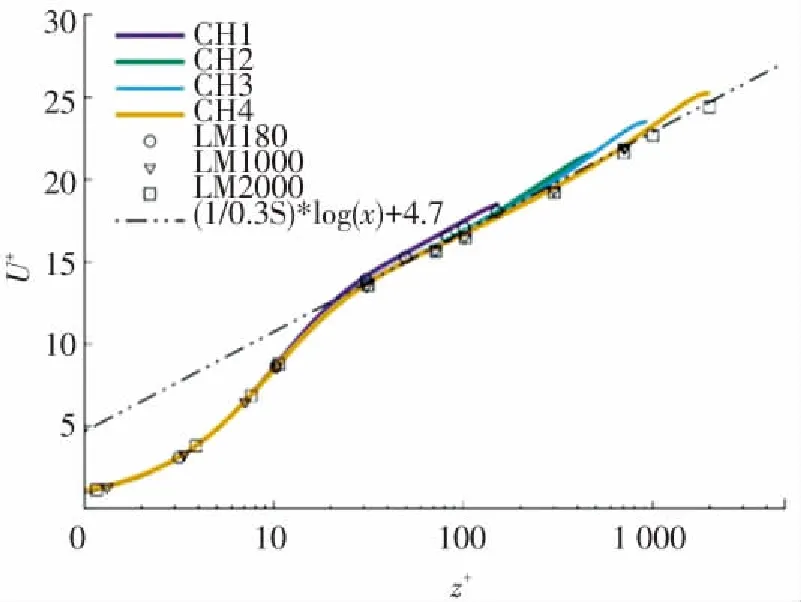
圖2 不同雷諾數下的平均速度曲線

2.2 雷諾應力張量

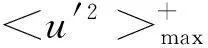
在比較+時同樣將所有算例的雷諾應力與Lee的結果進行了對比. 可以看出，雷諾正應力的最大值基本都出現在z+= 15的位置，而且隨著Re數的增大，雷諾應力也隨之增大. 本文的結果與Lee在2015年的DNS結果相近，可以證明本文結果的準確性.

Lozano等人[9]在文章中指出，流向方向的雷諾應力最大值與雷諾應力之間滿足以下關系：

(5)

由于CH1所計算的Reτ較小，規律與CH2～CH4的結果相比有所區別. 從圖3(b)上來看，本文CH2～CH4的結果同樣也滿足方程(5).

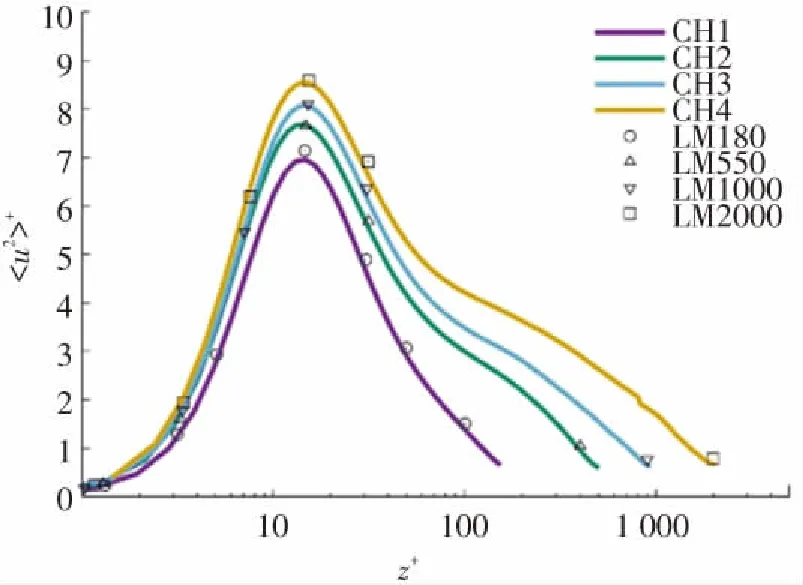
(a) 與Δx+的關系

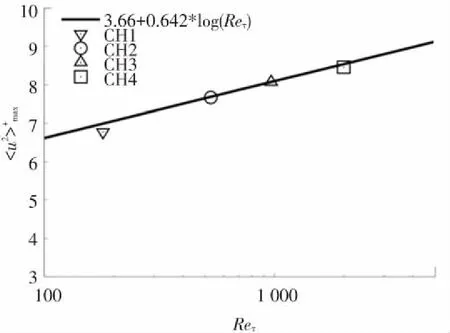
(b) 最大值隨著Reτ的變化

綜上所述，平均速度與雷諾正應力結果的對比情況表明，本文湍流槽道流的DNS計算結果是可信的.

3 局部特殊壁面邊界條件

湍流流動控制是目前最熱門的研究課題之一，壁面邊界是湍流流動控制的研究重點. 相較于常用的譜方法，速度壓力法壁面邊界條件易于處理是針對流動控制數值研究的一個優點，而計算精度問題則可以通過盡可能地提高計算規模來解決. 借助類似浸沒邊界法等計算技術，粗糙壁面、滑移壁面以及各種吹吸氣等壁面處技術都很容易實現.

為了探討壁面邊界條件變化對槽道湍流的影響，本文在CH1算例的基礎上進行初步嘗試. 在下壁面加入三排微小毛刺，采用浸沒邊界法實現，計算壁面局部變化對槽道湍流流動的影響. 本文采用離散力法計算浸沒邊界法中的力源項. 在N-S方程中加入虛擬力源項，在控制方程中加入體積力來替代邊界條件. 在計算過程中求解完投影法的速度壓力之后再加入虛擬力源項得到最終的速度.

如圖4所示，在周期邊界條件的槽道流中的1/4位置處，加入三排長寬約為0.044h(8個壁面單位)、高度約為0.022h(4個壁面單位)交錯排列的微小毛刺. 毛刺在整個展向具有微小間隔并均勻分布，在流向方向上對流動的影響只有局部作用.

圖4 槽道流加入粗糙毛刺示意圖

圖5給出的是在毛刺下游16個到320個壁面單位處的展向平均速度剖面，分別為毛刺高度4個壁面單位的4、10、20、40和80倍距離，同時給出了無毛刺時全場平均的速度分布. 在毛刺的作用下，鄰近位置的平均速度剖面線變化很大，平均速度曲線有所升高. 當遠離毛刺位置時，毛刺對湍流速度剖面的影響逐漸減小，到80倍毛刺高度距離位置處，湍流速度剖面已恢復到與無毛刺流動基本一致. 可見壁面條件的改變對湍流流動影響顯著.

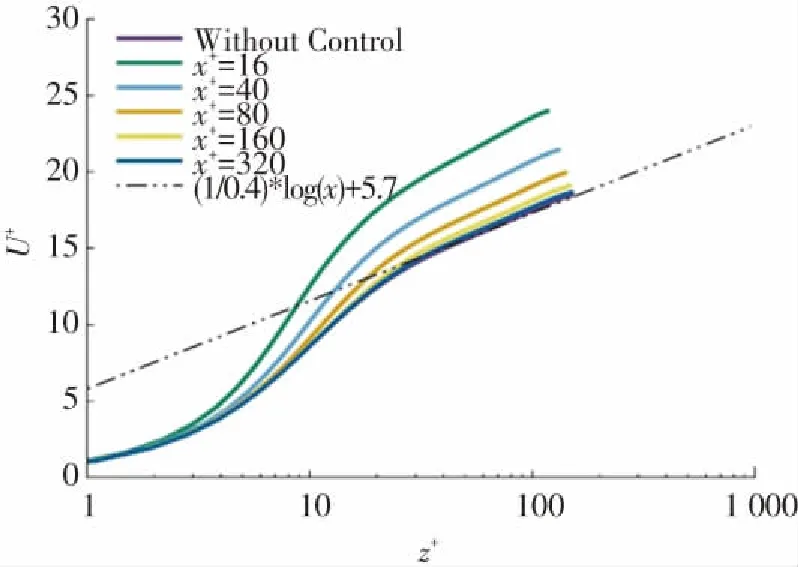
圖5 加入毛刺后不同位置的平均速度曲線

由此可見，本文的速度壓力法對湍流流動控制的研究，無論是加入展向的振動、壁面吹吸氣還是改變槽道流的壁面形狀都是易于實現的. 加上本文方法具有高效并行特點，可以開展規模巨大的高Re數湍流槽道流DNS模擬計算，為湍流流動控制研究提供有效的計算工具和有價值的數據.

4 結 論

建立了槽道流DNS計算的PDM-DNS方法，在“天河二號”超級計算機上使用256個CPU核進行計算，其規模超過109自由度，計算并行效率超過95%，并得到良好的線性加速比. 由此為開展高Re數湍流槽道流DNS模擬提供了有力的計算工具.

4個不同Re數的槽道流計算結果顯示，速度剖面都具有粘性底層和對數段分布，并與湍流速度對數段的理論預測值分布一致，雷諾正應力分布合理，所有計算結果與他人的DNS結果吻合. 本文提出的計算方法所得到的湍流槽道流計算結果和數據是合理可信的.

相較于譜方法，本文采用的速度壓力差分求解方法方便于復雜邊界條件的處理. 在下壁面加入局部毛刺的算例結果展示，結合浸沒邊界法等計算技術，本文方法可以擴展到復雜壁面條件的湍流流動控制等研究中.