顆粒驅動軟體驅動器設計及FEM-DEM運動分析

韓奉林, 李明輝, 田 亮, 劉 偉, 費 磊, 趙海鳴

(1. 中南大學 機電工程學院,長沙 410012；2. 中南大學 輕合金研究院,長沙 410012；3. 中南大學 高性能復雜制造國家重點實驗室,長沙 410012)

軟體機器人具有環境適應性好、人機交互安全、系統設計簡單等優點，因此獲得了廣泛的研究[1]. 現有軟體驅動器驅動模式主要包括：流體驅動[2]、介電彈性體[3]、形狀記憶合金[4]、化學過程驅動[5]、拉線驅動[6]等.

變剛度技術是軟體機器人走向應用的重要使能技術，有效調控剛度對于軟體機器人具有重要意義. 目前軟體機器人的變剛度實現機理包括拮抗原理[7-8]、電磁流變原理[9]、材料相變原理[10-11]及阻塞機制等，其中利用基于真空的顆粒阻塞機制由于結構簡單、剛度調節速度快的優點近年來得到廣泛的研究[12].

Cheng等[13]利用顆粒阻塞實現了微創手術柔性機械臂的局部剛度調控. Jiang 等[14]提出了一種柔性機械手，采用顆粒阻塞和氣動肌肉機構相結合的方法實現驅動和變剛度. Brown 等[15-16]利用顆粒阻塞設計了一種通用軟體抓手，能夠在沒有反饋的情況下抓取各種形狀的物體，此抓手操作容易、結構簡單，但是在抓取時，只能用力壓向被抓物，從而被動地順應被抓物形狀，所以當被抓物較軟或體積過大時，抓取效果不理想. Wei等[17]設計了一種包括氣動層和顆粒層的雙層結構軟體手指，氣動層實現驅動器的運動，而顆粒腔實現剛度調控. 為避免使用復雜的真空系統，Li 等[18]提出了一種被動顆粒阻塞的概念，在氣動腔內施加正壓，彎曲的驅動器會擠壓松散的顆粒使之阻塞，故可通過控制氣壓即可調節軟體驅動器的剛度.

在以上驅動器中，顆粒物質填充得比較松散，當發生阻塞轉換時，驅動器姿態會有所變化，保形能力下降. 為了解決這一問題，Li等[19]與韓奉林等[20]分別獨立地提出了顆粒驅動軟體驅動器，其中的顆粒物質始終充滿軟體型腔，顆粒的體積分數較高，所以在抽真空阻塞過程中，驅動器可以具有很好的形狀保持能力. 韓奉林等[20]發現通過調節腔內負壓，可使驅動器的剛度提升約2.75倍，但顆粒充入型腔時，會堵塞在型腔入口附近，從而在驅動器根部產生較大的徑向膨脹，導致驅動器彎角較小，需要通過結構優化進一步提升彎曲性能.

有限元法(Finite Element Method，FEM)是分析流體驅動軟體機器人運動的常用方法，但由于顆粒物質的離散性，直接采用有限元方法分析顆粒驅動軟體驅動器運動存在很大難度. 韓奉林等[20]采用Mohr-Coulomb(M-C)模型將顆粒物質描述為連續介質，繼而應用 FEM 方法成功分析了驅動器的變形過程，但由于M-C 模型過度簡化了顆粒物質，計算誤差較大. 在顆粒驅動軟體驅動器中顆粒物質的運動具有離散性，其流動需要采用離散元(Discrete Element Method, DEM)仿真方法分析；而彈性腔壁的變形具有連續性，其變形需要采用非線性FEM仿真方法分析，因此必須采用FEM-DEM耦合方法才能處理此類復雜非線性邊界問題. 目前FEM-DEM已用于分析金屬板材成型[21-22]、輪胎沙地接觸[23]、巖石開鑿[24]等問題，但是分析時更多的局限于單向耦合仿真，即DEM單向向FEM提供載荷，FEM不向DEM更新位移. 而在顆粒驅動軟體驅動器運動分析中，由于變形腔壁的大變形，必須使用FEM-DEM雙向耦合分析方法. 目前開展FEM-DEM雙向耦合計算的主流方法是通過第三方平臺為獨立的FEM和DEM分析軟件進行數據交換通道[25]，但這種方法實施難度大、效率低，精度損失也比較大.

本文有兩個目的：1)在單一ABAQUS平臺下，實現了顆粒驅動軟體機器人FEM-DEM的雙向耦合運動分析，通過與單純FEM分析和實驗結果對比，驗證這種方法的有益效果，并用這種方法研究了顆粒粒徑對機器人運動的影響規律；2)設計了一種具有徑向增強約束的軟體型腔，通過仿真和實驗，證明其可在不影響變剛度能力的前提下，增大機器人的運動范圍.

1 方法與材料

1.1 驅動器結構設計

文獻[20]中提出的顆粒驅動軟體驅動器腔體的原型結構如圖1(a)所示，在一定程度上驗證了顆粒驅動的可行性. 但如圖1(b)所示，在仿真和實驗中發現驅動器變形腔徑向膨脹效應顯著，造成彎曲角度較小. 如果能夠有效約束徑向膨脹，則有可能進一步增加彎曲角度，提升彎曲性能. 為此，本文設計了一種新型的結構如圖1(c)所示，在腔體外側增加6個硬度較高的加強筋，以限制腔體的徑向變形，增加顆粒對彎曲變形的作用效果.

(a)原型變形腔結構[20]

(b)原型結構仿真和實驗膨脹狀態

(c)設計的變形腔結構

圖2展示了包含顆粒輸送裝置的完整的驅動器并且標示出了驅動器的關鍵尺寸. 腔體與顆粒流道之間使用連接件進行連接. 步進電機通過絲杠螺母副帶動活塞在顆粒流道內往復移動.

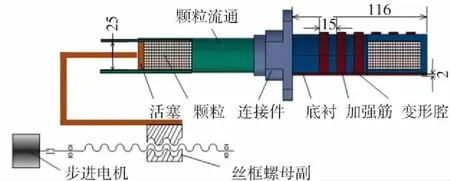
圖2 驅動器結構

驅動器工作循環分為驅動變形、承載和卸載3個階段. 驅動時活塞向右運動，將顆粒壓入變形腔，迫使驅動器開始驅動變形. 變形至預定位置后，通過抽氣孔將腔內抽成負壓，提高承載能力. 卸載時腔內與大氣連通，活塞向左運動，顆粒在變形腔彈性恢復力擠壓下流回顆粒流道.

1.2 驅動器材料選擇和樣機制備

驅動器使用的材料如圖3所示. 為了減小顆粒間的摩擦、提高顆粒的傳壓能力，選擇質地較硬且表面光滑的φ2.8 mm的亞克力球作為填充顆粒，如圖3(a)所示. 彈性變形腔體材料選擇雙組份硅膠Ecoflex 00-30(Smooth-on)材料(見圖3(b))，該材料邵氏硬度較低，可制造性及彈性好，在氣動變形腔設計中應用較為廣泛. 為了起到更好的限制變形的效果，本文底襯和加強筋均選取邵氏硬度較高的聚氨酯材料(PU),如圖3(c)所示.

(a)亞克力球 (b) 彈性硅膠材料 (c) 聚氨酯材料

驅動器制備過程見圖4. 首先在CAD中建立澆注模具的模型，采用光固化3D打印技術打印模具如圖4(a)所示. 分別量取等體積Ecoflex 00-30A、B組分硅膠均勻混合，隨后放入真空除氣裝置中進行第一次脫氣處理，將硅膠材料澆入模具內,如圖4(b)所示. 待澆注完成后，將模具放入真空除氣裝置內進行第二次除氣處理. 將模具靜置成型3～4 h，待硅膠成型后做脫模處理(見圖4(c))，加強筋和底襯是由圖4(d)中的材料使用裁刀直接裁剪而成，然后使用硅膠專用膠(E300，佛山一滴強膠粘劑有限公司)將其與型腔粘接固定，圖4(e)中的連接件通過3D打印而成，將驅動器整體和連接件使用綁帶固定，最后裝配得到的驅動器如圖4(f)所示.

(a)打印的摸具 (b) 硅膠澆注 (c) 脫模后的腔體 (d) 加強筋和底襯材料 (e) 連接件 (f) 裝配后的驅動器

如圖5所示，用于澆注制造變形腔體的模具主要由四部分組成：內模(由內左、右模組成)、外模(由外左、右模組成)、底模和模芯. 其中內模在澆注成型過程中形成腔體的外部形狀，模芯在澆注過程中形成腔體的內部流道，外模和底模上布有定位銷，起對內膜以及模芯的定位作用.

1.3 顆粒驅動軟體驅動器的 FEM-DEM 仿真

在ABAQUS中，提供了一種能夠描述剛性顆粒的PD3D單元，此單元可以用于模擬大量離散顆粒相互接觸運動，結合ABAQUS 強大的非線性有限元功能可以有效進行DEM-FEM耦合仿真，故可以很好地用于顆粒驅動軟體驅動器的顆粒充填型腔過程和驅動器變形過程的仿真研究.

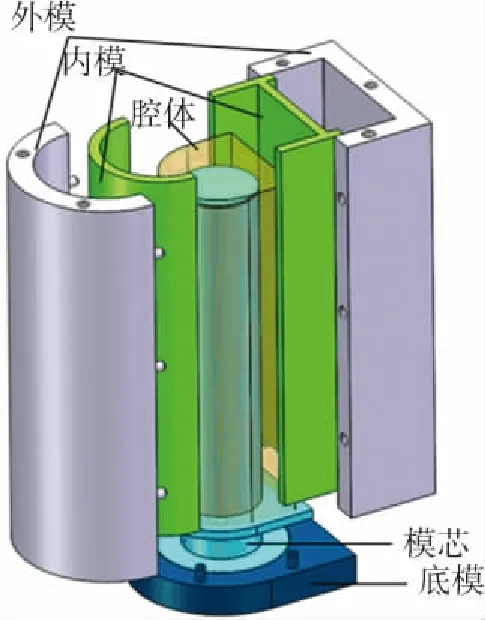
圖5 變形腔模具

為獲得準確的仿真結果，需要建立超彈性材料的本構模型. 超彈性材料本構模型參數值通過單軸拉伸試驗獲得，采用Ogden 模型擬合出最優的聚氨酯材料、Ecoflex 00-30本構模型. 參數見表 1.

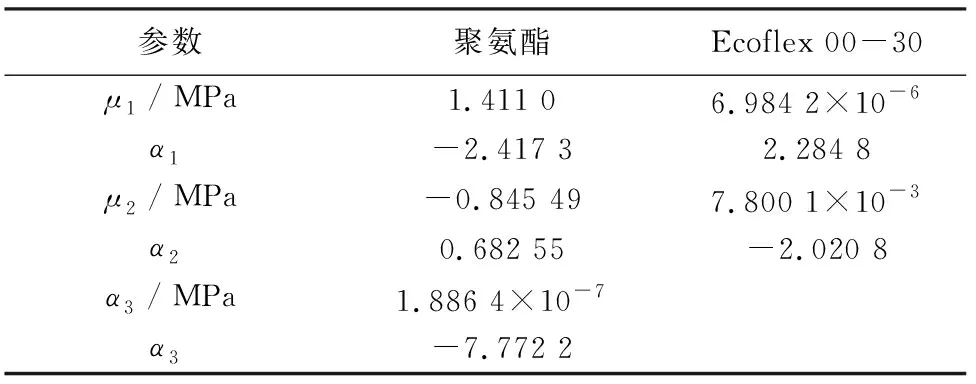
表1 超彈性模型參數

設置合理的接觸模型是準確進行DEM仿真的前提. 本文使用Hertz接觸模型來定義顆粒的接觸屬性. 對于同一種球型顆粒，由Hertz接觸理論得出法向接觸力與法向位移間的關系表達式為

(1)

顆粒接觸剛度為

(2)

由于ABAQUS CAE 可視化界面不支持PD3D單元的設置，故需要先在可視化界面中完成除顆粒外其余幾何體的建模、材料屬性的設置、網格的劃分等前處理工作. 在仿真中將活塞、顆粒流道、連接件設置為剛體. 將變形腔、筋、底襯均設置為C3D8R單元，網格數目分別為4206、96、468. 完成前處理設置后生成inp文件，然后需要對inp文件進行修改，以完成顆粒生成、顆粒屬性設置等工作. 修改inp文件主要流程見圖6，仿真采取顆粒生成器(Particle generator)的方法生成顆粒. 首先定義活塞端面為顆粒生成器，顆粒最大數目定義為20000，然后定義顆粒直徑、彈性模量、泊松比. 再定義顆粒Hertz接觸，最后定義顆粒生成速率、顆粒移動速率等. 生成顆粒前后的型腔模型如圖7所示.

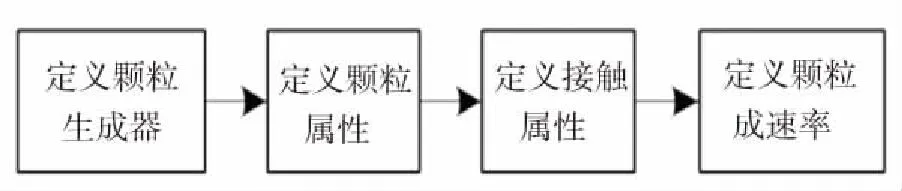
圖6 修改 inp 文件流程

(a)

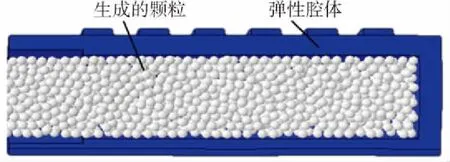
(b)

1.4 基于 M-C 彈塑性模型的FEM仿真方法

文獻[20]中將顆粒物質作為連續體，提出了一種針對顆粒驅動軟體驅動器的FEM仿真方法. 為了對比FEM和DEM-FEM兩種分析方法的準確性，采用FEM方法對設計的驅動器進行對比仿真分析. 顆粒材料的本構模型采用彈性模型與M-C塑性模型的聯合彈塑性模型. 其中彈性模型參數彈性模量、泊松比見 1.3節.

在塑性本構模型中，一般認為，顆粒材料的破壞符合粉體或土體的莫爾-庫倫(Mohr-Coulomb，M-C)破壞準則. M-C強度理論公式為

τ=c+σtanφ.

(3)

其中φ為法向應力，為τ剪應力. 亞克力球的內摩擦角φ和黏聚力c通過快剪試驗獲得，實驗中試樣剪切速率 0.64 mm/min，實驗停止條件為試樣軸向應變達到 20%，測得的φ=26.1°，c=0.

1.5 軟體驅動器性能測試實驗

1.5.1 實驗設計

為驗證所提出的仿真方法的有效性和設計方案的合理性，設計了兩組實驗研究顆粒驅動器的性能： 第一組實驗研究設計的驅動器結構的彎曲性能；第二組實驗研究軟體驅動器在不同真空負壓狀態下(阻塞)剛度變化情況. 實驗中使用顆粒的粒徑為φ2.8 mm.

本研究中設計制造的用于分析驅動器彎角和剛度的實驗裝置如圖8所示. 驅動器垂直放置，依靠連接件固定在臺架上，兩個直線模組分別沿水平和豎直方向安裝，其上都安裝有測力計. 豎直直線模組帶動測力計下移同時推動活塞移動，移動距離可通過計算機控制. 將水平模組和測力計用于剛度試驗. 配備真空泵和真空調壓閥，通過氣管與驅動器連接，為其提供負壓.

圖8 軟體驅動器性能測試裝置

1.5.2 彎曲角度的表征與測量

驅動器彎曲角θ的定義見圖9，其中狀態1為驅動器的初始狀態，狀態2為變形后狀態，彎曲角θ為驅動器端面與y軸的夾角. 在實驗中，由于實驗條件的限制，活塞移動的最大距離為90 mm，每次將活塞移動10 mm，實驗過程中使用相機采集驅動器圖像，使用 MATLAB 圖像處理功能測量彎曲角度并記錄，重復9次測量過程直到活塞位移至90 mm.

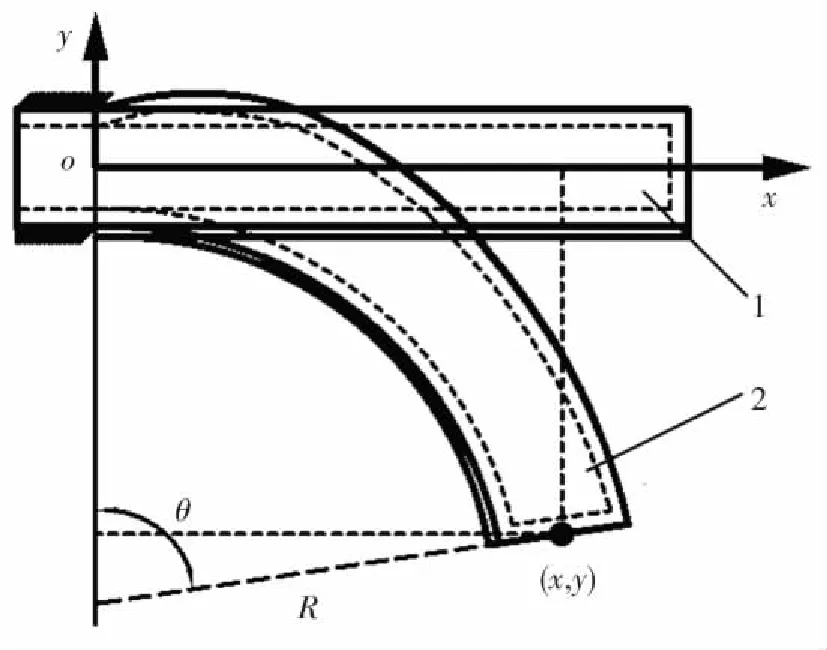
圖9 驅動器彎曲角定義

1.5.3 彎曲剛度的表征與測量

在文獻[19]中，采用如下方法表征驅動器的彎曲剛度：通過測力計推動驅動器末端產生位移δy，此間驅動器彎角為δβ(β=arctan(y/x)為文獻[19]中定義的彎曲角)，測力計最大輸出值為F，定義SR=Fδy/δβ表示驅動器的彎曲剛度. 當β和δy較小時，驅動器末端的x坐標近似為常數，且δβ≈(y+δy)/x-y/x=δy/x，因此，SR與F之間只差一個常系數. 在本文中，為簡單起見，直接以F作為彎曲剛度的表征參數.

實驗中，首先使控制豎直直線模組移動60 mm距離，使驅動器產生對應的彎曲，然后啟動真空泵使腔內產生負壓并使顆粒阻塞. 再控制水平直線模組移動，使測力計拉動驅動器勻速移動20 mm，重復3次并且記錄每次實驗的拉力的最大值，將3組最大拉力的平均值作為表征彎曲剛度的參數. 然后改變真空泵的負壓值，重復整個實驗過程. 本文選取負壓為0、-20、-40、-60、-75 kPa的情況進行測量.

2 結果與討論

2.1 彎曲性能仿真和實驗結果

為對比兩種仿真方法分析計算驅動器變形的準確性，在本研究中使用 FEM 和 FEM-DEM 兩種仿真方法分別對驅動器進行了分析并進行了實驗.

FEM仿真應力云圖如圖 10(a)所示，DEM-FEM 仿真應力云圖如圖 10(b)所示，圖 10 中還展示出了在活塞位移分別為0、20、40、60、100 mm時驅動器的變形狀態. 圖 11 是驅動器在不同活塞位移下的彎曲實驗結果，仿真和實驗結果對應的驅動器彎角與活塞位移關系曲線如圖12所示. 實驗中當活塞位移為90 mm 時，驅動器彎曲角度為72.7°，對比文獻[20]中原型驅動器結構角度48.9°，彎曲角度提升了48.7%.

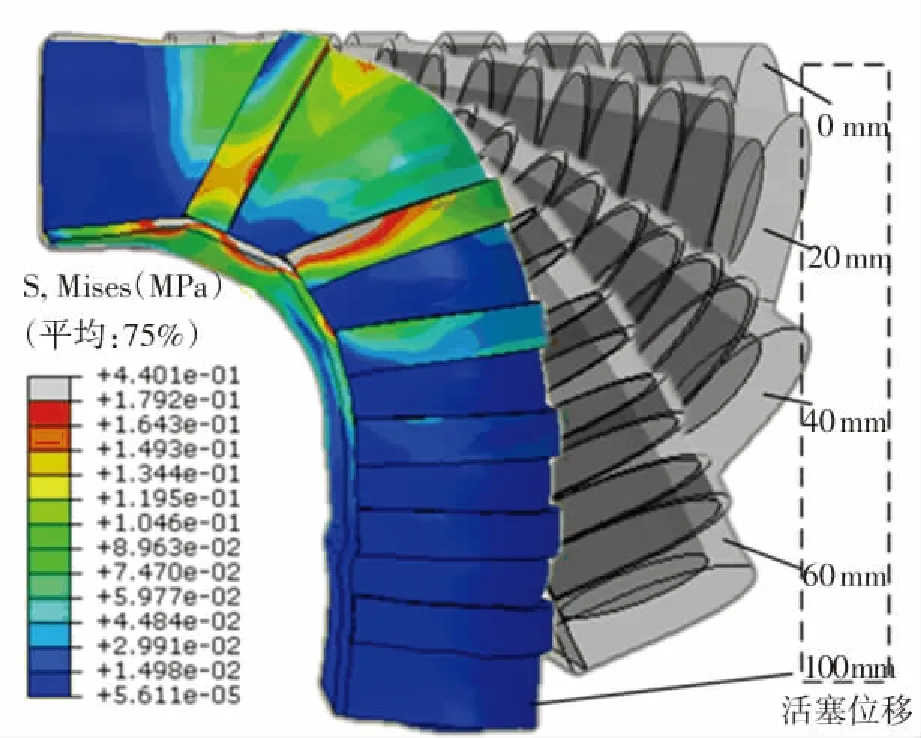
(a)FEM仿真結果

(b)FEM-DEM 仿真結果

圖11 驅動器彎曲實驗結果

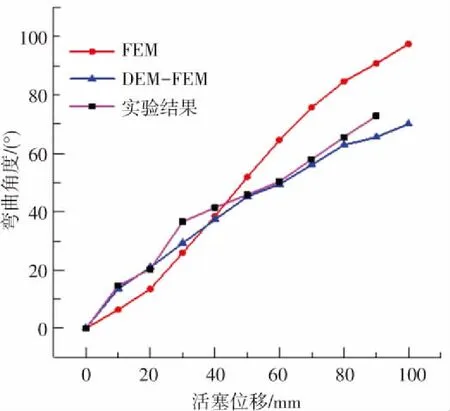
圖12 驅動器彎角與活塞位移關系的實驗和仿真結果

從圖12 中曲線整體可看出,FEM-DEM仿真結果相對于FEM仿真結果更加接近于實際情況. 除此之外，活塞位移90 mm時，驅動器的FEM仿真彎角為90.76，FEM-DEM仿真的彎曲角度為 65.1°，對于驅動器采取FEM-DEM方法計算的彎曲角度與實驗相比誤差為 10.5%. FEM仿真的誤差為 24.8%. FEM-DEM比FEM仿真結果驅動器彎曲角度更小，同時誤差減小了 14.3%. 這可能是因為基于M-C模型的FEM方法過度簡化了顆粒物質，造成計算誤差較大. 而FEM-DEM方法與實驗仍存在誤差的原因可能是仿真中設置的顆粒之間的摩擦特性、超彈材料的本構模型等條件與實際情況存在一定的差異.

從圖10(a)和(b)可以看出，FEM-DEM 仿真中的驅動器應力分布較為均勻且驅動器末端也有著明顯的應力，整體彎曲效果較為平滑，曲率變化較小. 而 FEM 仿真中驅動器局部應力較大，應力和彎曲都集中在靠近驅動器根部的第一個筋和第二個筋之間且在驅動器末端應力很小. 這可能是由于FEM-DEM仿真內部顆粒材料流動性較好，而FEM方法過高地估計了顆粒間的摩擦力導致腔體內部顆粒流動性較差. 顆粒在驅動器根部堆積，局部產生了較大的應變，造成了局部彎曲. 并且隨著活塞位移的增加，堆積的顆粒越多，局部彎曲越大.

與單純FEM方法相比，FEM-DEM方法的另一個優勢在于可以研究顆粒粒徑對驅動器變形的影響規律. 本研究中使用FEM-DEM方法對顆粒直徑為4、2.8、2 mm 的情況進行仿真，仿真計算獲得不同顆粒直徑對于驅動器彎曲角度的影響關系如圖13所示. 可以看出活塞位移超過10 mm后驅動器彎角呈現出近似線性的變化，這種現象可能是由于活塞移動一定的位移后驅動器內部顆粒變得更加緊湊造成的，當注入顆粒體積較小時，顆粒之間存在較大間隙，而當更多的顆粒被注入驅動器時,彎曲角度的變化線性度更好.

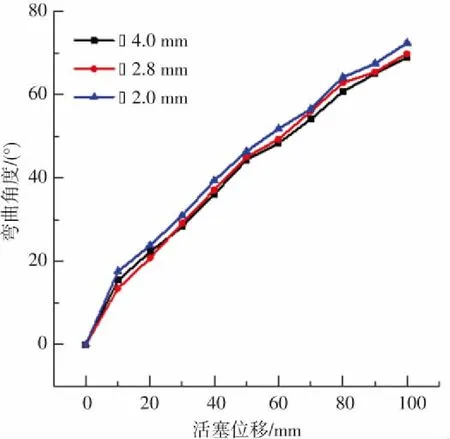
圖13 顆粒直徑對驅動器彎角-活塞位移關系的影響

此外，可以看出使用直徑為2 mm的顆粒的驅動器在活塞每一個位移狀態下的彎角均是最大的，并且在活塞位移超過30 mm時，顆粒直徑越小，驅動器彎曲角度越大. 這種現象可能是因為對于相同的腔壁面積，直徑較小的顆粒可以有更多的接觸點數，而較大的顆粒分布更加稀疏，造成了傳力效果的不均勻.

2.2 剛度變化實驗結果

圖14 是驅動器在不同負壓下，末端受拉產生20 mm位移過程中所施加的最大拉力，拉力越大則表明驅動器的剛性越強. 從中可以看出,隨著負壓力的增加驅動器所能夠承受的拉力增大，且變化是近似線性的. 除此之外，本研究中的驅動器在負壓為0時最大拉力約為3.1～3.5 N，在負壓為-75 kPa時最大拉力約為8.1～8.3 N，可知驅動器在阻塞前后承載力有著大約2.7倍的提升，即剛度變化也約2.7 倍. 相對于文獻[20]中原型驅動器結構，本設計中增加的徑向增強約束并沒有削弱驅動器的剛度調節能力.

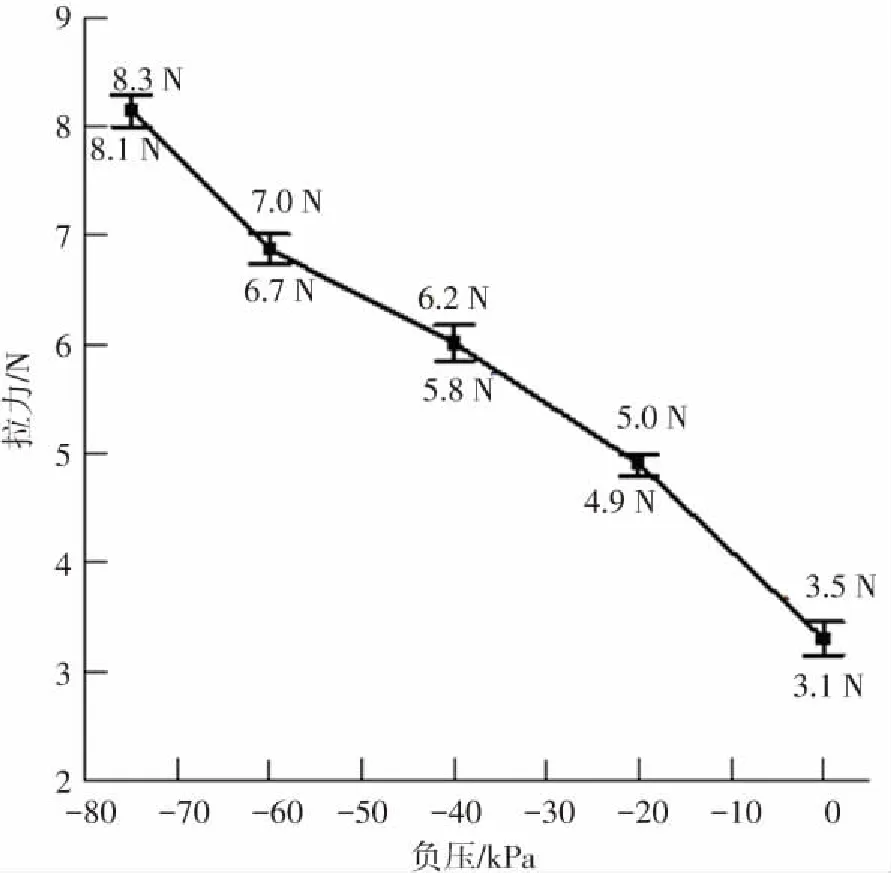
圖14 驅動器負壓-拉力關系的實驗結果

3 結 論

本文提出了一種以顆粒物質為介質驅動的軟體驅動器，為減弱局部徑向膨脹效應，其型腔設計有徑向增強約束. 為在設計階段能更準確地預測驅動器地變形規律，將FEM-DEM雙向耦合計算方法應用于驅動器的運動過程仿真，主要結論如下：

1)在ABAQUS單一平臺下，成功實現了顆粒驅動軟體驅動器變形過程的FEM-DEM雙向耦合仿真.

2)與基于M-C模型的單純FEM方法相比，DEM-FEM耦合計算所得的驅動器彎曲角度計算誤差降低了14.3%，說明FEM-DEM雙向耦合仿真能夠更為真實地刻畫顆粒物質流動與超彈型腔大變形之間的協同規律，是驗證顆粒驅動軟體機器人變形狀態的較優手段.

3)通過FEM-DEM雙向耦合仿真研究發現,較小的顆粒粒徑可以增強機器人的變形能力.

4)仿真和實驗結果表明,徑向增強約束可使驅動器最大彎曲角度提升約48.7%，且對變剛度能力無不良影響.

5)本文僅開展了顆粒驅動軟體機器人運動和變剛度規律的初步研究，這種機器人在多次往復運動中的重復定位精度、剛度演化等重要規律還有待進一步研究.