高超聲速環(huán)境D6AC鋼結(jié)構(gòu)多物理場耦合模擬

王文瑞，葉 偉，王 帥，溫曉東

(1. 北京科技大學 機械工程學院, 北京 100083；2. 北京科技大學 流體與物質(zhì)相互作用教育部重點實驗室, 北京 100083；3. 中國航天科工集團有限公司磁懸浮與電磁推進技術(shù)研究院, 北京 100143；4. 天津航天機電設(shè)備研究所，天津 300301)

高超聲速飛行器服役時，由于空氣壓縮，產(chǎn)生大量內(nèi)能，同時氣流與熱防護材料表面劇烈摩擦，產(chǎn)生大量摩擦熱，在材料表面形成一個高溫高壓的極端環(huán)境，導(dǎo)致飛行器結(jié)構(gòu)內(nèi)部產(chǎn)生大溫度梯度，進而引起飛行器結(jié)構(gòu)材料失效. 材料失效會降低飛行穩(wěn)定性，影響飛行器服役安全，因此研究熱防護材料在多物理場耦合作用下的失效問題具有重大意義. 為了深入分析材料失效，本文將開始實驗至D6AC鋼材料破壞的時長定義為安全飛行時間[1-3].

Ognjanovic等[4]利用ANSYS Workbench建立了導(dǎo)彈結(jié)構(gòu)的熱流固耦合分析模型，研究了在2.3和3.7馬赫數(shù)下氣動力和氣動熱對結(jié)構(gòu)變形的影響，并通過靜態(tài)結(jié)構(gòu)試驗對模擬結(jié)果進行了驗證，結(jié)果表明氣動熱對結(jié)構(gòu)變形的影響遠大于氣動力. 董維中等[5-7]建立了初步的表面溫度分布與氣動熱耦合計算方法，以C-C為表面材料，考慮熱化學非平衡和表面溫度分布的因素，研究了C-C燒蝕對再入體頭部區(qū)域的壁面溫度和熱流分布的影響，而后又采用多種氣體模型算法，并討論了它們對激波脫體距離、壁面熱流、溫度和密度分布等的影響. 李樺等[8]運用了Baldwin-Lomax湍流模型，計算了在攻角為5°時鈍錐體迎風面的壓力分布和橫向噴流干擾流場的數(shù)值解. 劉建霞等[9]分析了高超聲速滑翔飛行器表面流場特征，并對典型工況下的氣動性能開展數(shù)值模擬研究，發(fā)現(xiàn)飛行器表面受熱存在明顯的分區(qū)特征，應(yīng)進行不同的熱處理方法.

目前的研究主要針對較低馬赫數(shù)下的工況，且沒有試驗進行對比和佐證. 本文基于高超聲速氣動力學和結(jié)構(gòu)力學基本理論，建立高超聲速熱防護結(jié)構(gòu)的多物理場耦合理論模型，通過數(shù)值模擬得到D6AC鋼在不同飛行環(huán)境中的安全飛行時間，并對模擬結(jié)果進行風洞試驗驗證，形成高超聲速飛行器多物理場耦合分析方法，以降低飛行試驗和風洞試驗實施困難及高成本的問題，同時以此方法為基礎(chǔ)，深入探究在不同飛行速度、飛行迎角、飛行高度以及飛行器形狀下的安全飛行時間.

1 高超聲速環(huán)境下D6AC鋼多場耦合理論模型

將高超聲速熱防護材料結(jié)構(gòu)的計算域分成流體域和D6AC固體域，如圖1所示.

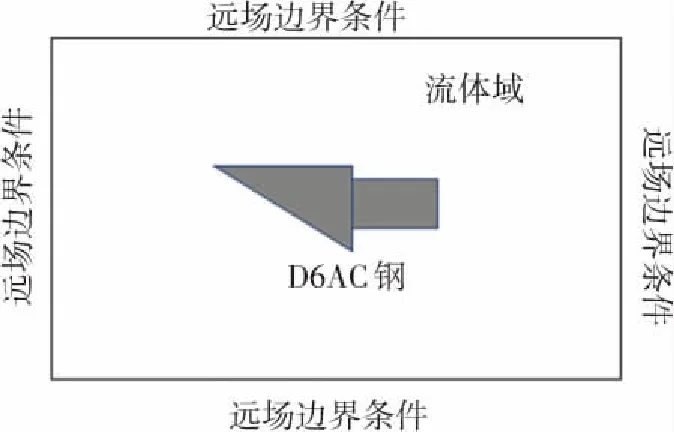
圖1 D6AC鋼結(jié)構(gòu)計算區(qū)域示意圖

在高馬赫數(shù)下，空氣屬于粘性可壓縮流體，因此流場的運動滿足納維-斯托克斯(Navier-Stokes)方程，包括質(zhì)量守恒方程、動量守恒方程和能量守恒方程. 質(zhì)量守恒方程的一般形式為[10]

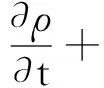
(1)

這里

(2)

式中:ρ為密度，單位kg·m-3；t為時間，單位s；·(ρV)為空氣動量的散度，是描述空氣從周圍匯合到某一處或從某一處流散開來程度的量；u,v,w為速度在3個坐標軸上的分量，單位m·s-1.

動量守恒方程的一般形式如式(3)所示:

(3)

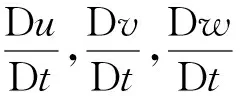
根據(jù)剪切應(yīng)力公式可以知道剪切應(yīng)力與速度隨距離的變化率成正比，如式(4)所示：

(4)

式中，μ為粘性系數(shù)，單位為N·s·m-2.

粘性應(yīng)力的表達式為

(5)

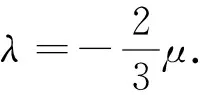
高馬赫數(shù)下的氣體是可壓縮、有粘度的，因此在守恒方程中有粘性力和壓力做功. 能量守恒方程如式(6)所示:

(6)

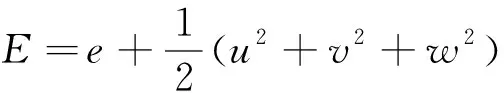
Q為3個方向的面積力做的功，如下:

(7)

q為3個方向的傳導(dǎo)熱功率，由傅里葉定律給出，如式(8)所示[11]：

(8)

式中:κ為熱傳導(dǎo)系數(shù)，單位為W/(m·K)；T為溫度，單位為K.

在高馬赫數(shù)下，溫度會逐漸升高，粘性系數(shù)和熱傳導(dǎo)系數(shù)都是關(guān)于溫度的單調(diào)遞增函數(shù)，溫度越高，空氣中分子運動越劇烈，粘性和熱傳導(dǎo)系數(shù)也隨之增大. 粘性系數(shù)由薩特蘭(Sutherland)公式確定，如式(9)所示:

(9)

式中:T0=288.15 K，C=110.4 K，μ0=1.8247×10-5kg/(m·s).由此可以確定在任意溫度下空氣的粘性系數(shù)值.

熱傳導(dǎo)系數(shù)由普朗特數(shù)Pr和粘性系數(shù)確定，如式(10)所示[12]:

(10)

式中:cp為定壓比熱，單位為J/(kg·K).

劇烈的氣動加熱使得結(jié)構(gòu)表面溫度急劇升高，同時熱傳導(dǎo)使得結(jié)構(gòu)內(nèi)部出現(xiàn)溫度梯度，由于熱膨脹及結(jié)構(gòu)約束的作用，結(jié)構(gòu)會產(chǎn)生熱應(yīng)力，進而發(fā)生變形. 結(jié)構(gòu)的響應(yīng)方程可表示為式(11):

[σ]=[D][B]δ=[S]δ.

(11)

式中:[D]為彈性矩陣，[B]為應(yīng)變矩陣，[S]為應(yīng)力矩陣，δ為位移矩陣. 在高超聲速結(jié)構(gòu)受到氣動力和氣動加熱的共同作用，結(jié)構(gòu)的總應(yīng)變量既包括氣動力引起的彈性應(yīng)變，也包括氣動熱引起的熱應(yīng)變.

2 D6AC鋼多場耦合模擬與驗證

D6AC鋼結(jié)構(gòu)工作時，氣動加熱過程是持續(xù)的、非穩(wěn)態(tài)以及非線性的，流場、溫度場和結(jié)構(gòu)場之間相互耦合作用. 以往的求解是將整個耦合作用過程分成三個部分來計算，但實際過程是連續(xù)的、反復(fù)循環(huán)的，使用拆分方法模擬出的結(jié)果有較大誤差. 所以本文采用流熱固耦合解法進行高超聲速結(jié)構(gòu)多場耦合問題模擬，同時建立流體模型和結(jié)構(gòu)模型，流體域和固體域在耦合面實時交換數(shù)據(jù)，實現(xiàn)流場和結(jié)構(gòu)場的同步計算. 耦合模擬過程如圖2(a)所示，給定初始的流體域溫度、壓強、來流速度及耦合面上的溫度分布，固體壁面為無滑移邊界條件，同時求解連續(xù)方程、動量和能量守恒方程，得到流體域的熱流分布和壓力分布；然后通過數(shù)據(jù)插值將流體域的熱流和壓力數(shù)據(jù)映射到結(jié)構(gòu)域網(wǎng)格上，作為結(jié)構(gòu)場求解的邊界條件，基于有限元仿真得到結(jié)構(gòu)溫度分布及結(jié)構(gòu)位移；再通過數(shù)據(jù)插值將結(jié)構(gòu)場的溫度分布和位移信息映射到流體域網(wǎng)格，作為邊界條件進行流體域的求解，直至達到所需的耦合計算時間. 流熱固耦合模擬模型如圖2(b)所示，高超聲速外流場求解采用基于有限體積法的Fluent求解器，結(jié)構(gòu)場求解采用Ansys Workbench中的Transient Structural求解器，流固耦合面的數(shù)據(jù)交換通過System Coupling模塊實現(xiàn). 仿真過程中，采用流體域和固體域一體化建模的方法，使得流體和固體區(qū)域在耦合面上的網(wǎng)格大小和節(jié)點位置均相同，避免了網(wǎng)格不匹配帶來的數(shù)據(jù)差值傳遞誤差，使計算結(jié)果更準確.

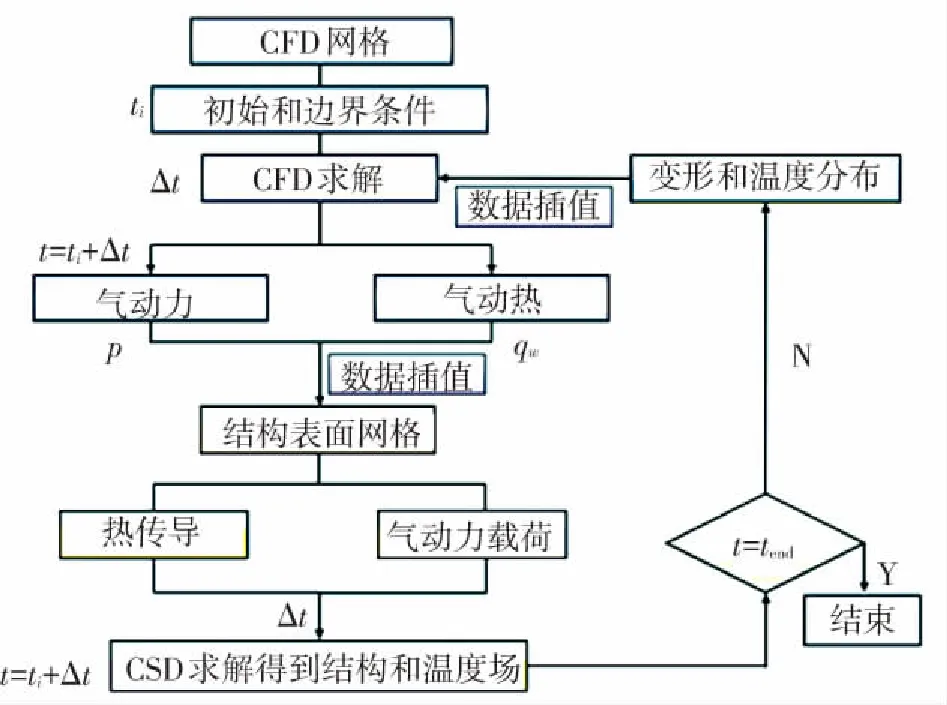
(a)流熱固耦合數(shù)據(jù)傳遞過程

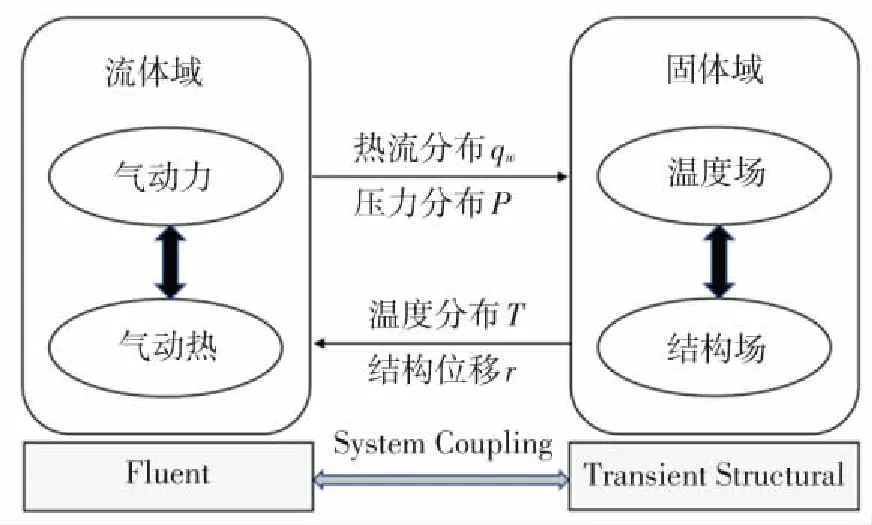
(b)流熱固耦合模型

2.1 風洞噴管流場模擬

為驗證本文D6AC鋼耦合分析方法的適用性和準確性，針對風洞進行空載模擬和試驗驗證，得到出口流場參數(shù)，并將其作為D6AC鋼結(jié)構(gòu)多物理場耦合計算的邊界條件，模擬流程如圖3所示. 對風洞噴管進行結(jié)構(gòu)化網(wǎng)格劃分，網(wǎng)格數(shù)量為31826，質(zhì)量均大于0.98. 噴管入口邊界條件為壓力入口(Pressure-Inlet)，出口邊界條件為壓力出口(Pressure-Outlet)；壁面為絕熱壁面邊界條件(Wall)；對稱面為對稱邊界條件(Symmetry). 通過數(shù)值模擬得到三組噴管出口參數(shù)，包括出口馬赫數(shù)、出口溫度和出口壓強，如表1所示. 以表1工況3為例，計算得到噴管出口處的馬赫數(shù)分布和溫度分布，如圖4所示.

圖3 D6AC鋼模擬流程

表1 噴管流場參數(shù)

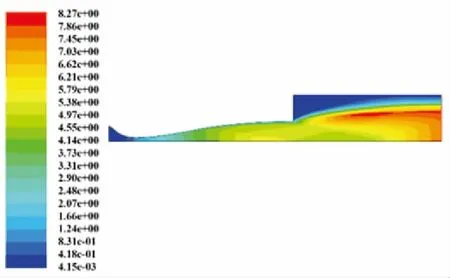
(a)噴管馬赫數(shù)分布

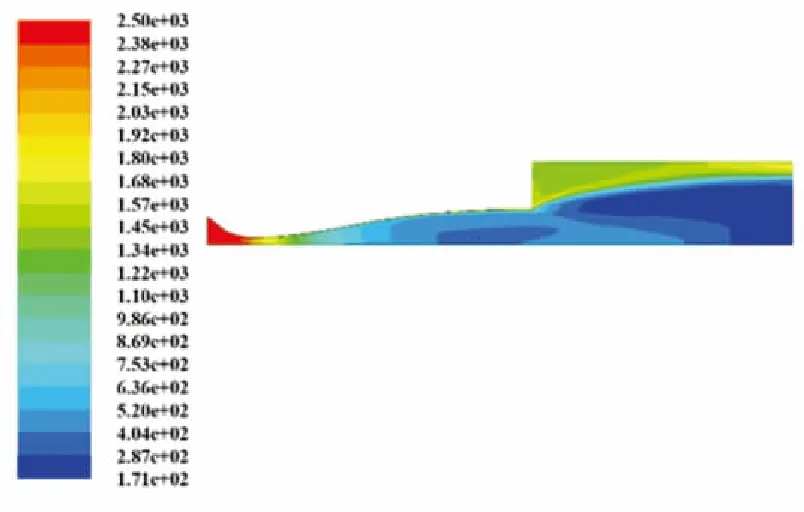
(b)噴管溫度分布

風洞噴管試驗如圖5所示. 由于皮托管本身對氣流有阻礙作用，所以它測量的總壓值是流場在產(chǎn)生激波后的流場總壓值，而非實際總壓值. 根據(jù)式(12)可得到流場實際的總壓值為

(12)

式中:PT為皮托管測量值，單位為MPa；P0為測點靜壓測量值，單位為Pa[13].

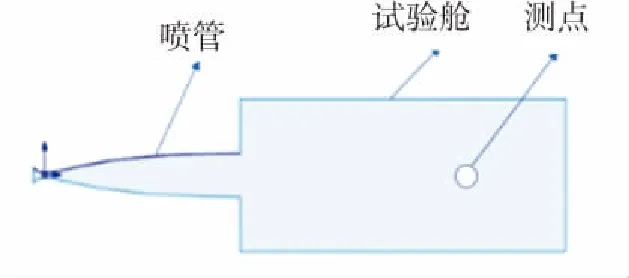
圖5 風洞噴管示意圖

表2 噴管模擬-試驗靜壓對比

三種工況下噴管測點換算的靜壓值與模擬得到的靜壓值進行對比，如表2所示. 可以看出，在噴管測點靜壓誤差分別為3.2%，3.5%，0.8%.

2.2 高超聲速環(huán)境D6AC鋼流場模擬

結(jié)構(gòu)材料為超高強度合金結(jié)構(gòu)鋼D6AC，密度為7 900 kg·m-3，楊氏模量為1.2×1013Pa，熱膨脹系數(shù)為1.68×10-5K-1，泊松比為0.3，其他材料參數(shù)如表3所示. 初始溫度設(shè)置為300 K，流體為理想氣體，具體參數(shù)如表1所示，將噴管出口流場參數(shù)設(shè)置為遠場壓力邊界條件，研究內(nèi)部響應(yīng)時，選擇尾端作為固定面，將初始溫度設(shè)置為300 K，流體為理想氣體. 幾何尺寸如圖6所示，采用ICEM軟件進行結(jié)構(gòu)化網(wǎng)格劃分，網(wǎng)格總數(shù)為831 246，其中D6AC鋼結(jié)構(gòu)網(wǎng)格數(shù)為94 826，流體域網(wǎng)格數(shù)為736 420.

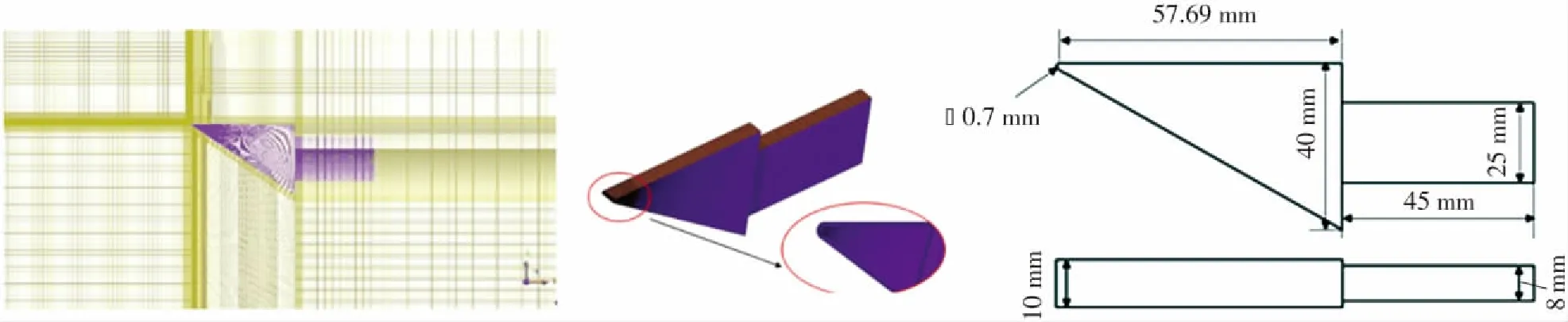
(a)計算域網(wǎng)格放大圖 (b)固體域網(wǎng)格放大圖 (c)D6AC鋼尺寸

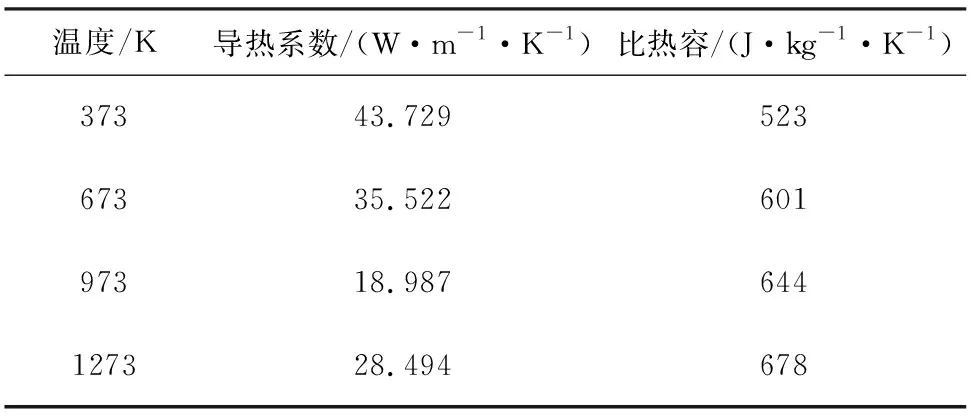
表3 D6AC鋼主要參數(shù)

根據(jù)建立的模型進行計算，總計算時間為40 s. 在不同工況下，D6AC鋼外流場溫度和壓力分布的趨勢相同，這里僅以表1工況2為例. 由于結(jié)構(gòu)前緣倒角為0.7 mm，對來流的阻滯作用較弱，所以在前緣形成了附體激波，且斜激波為主要形式，正激波的范圍較小，如圖7所示. 激波后氣流溫度和壓力發(fā)生急劇變化，在頭部形成一個局部高溫區(qū). 尾部下端不是平滑過渡，發(fā)生了激波與膨脹波的摻混和引射，并造成了附面層分離，貼近壁面的區(qū)域為低速流動，遠離壁面的區(qū)域為高速流動，形成渦流.

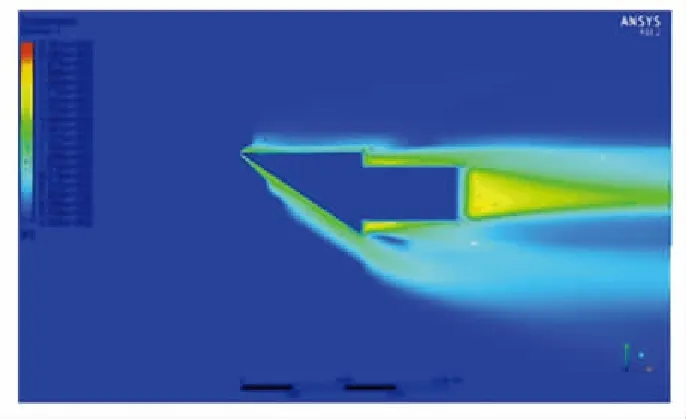
(a) 20 s時流場溫度分布

(c)20 s時流場壓力分布

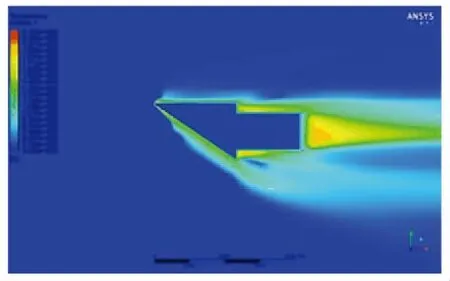
(b)40 s時流場溫度分布

(d)40 s時流場壓力分布

圖8為三種工況下結(jié)構(gòu)前緣駐點溫度隨時間變化的曲線，可以看出駐點溫度隨時間的推移逐漸升高，這是由于在外流場氣動加熱作用下，氣動加熱產(chǎn)生的熱量不斷向結(jié)構(gòu)內(nèi)部傳遞，導(dǎo)致結(jié)構(gòu)溫度不斷升高. 開始時駐點溫度升高地較快，之后逐漸降低，這是由于在氣動加熱初期，流體與結(jié)構(gòu)溫差較大，熱流密度也較大，隨著結(jié)構(gòu)溫度的升高，附面層內(nèi)的溫度梯度逐漸減小，使得壁面熱流密度逐漸下降，溫升速率也隨之減小，最終結(jié)構(gòu)的溫度場將達到穩(wěn)定狀態(tài). 此外，來流溫度越高，相應(yīng)的駐點溫度也越高.

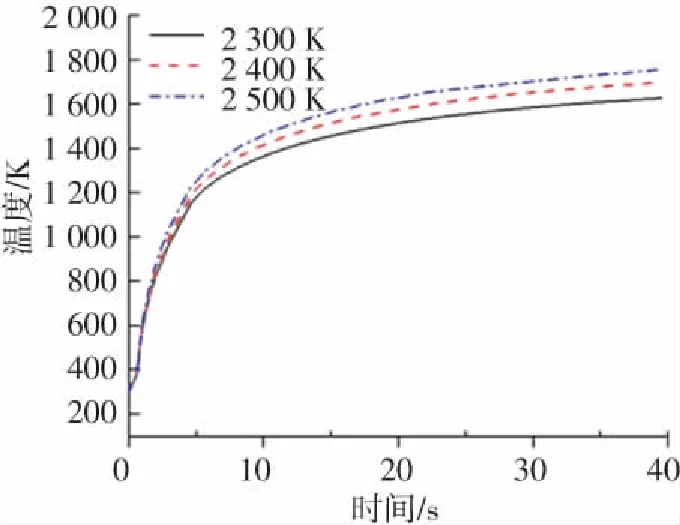
圖8 前緣駐點溫度隨時間變化曲線

2.3 D6AC鋼模擬結(jié)果驗證

風洞試驗采用北京科技大學“極端特殊環(huán)境下材料及構(gòu)件實驗評價科學裝置”，如圖9(a)和圖9(b)所示，風洞尺寸與模擬計算相同，通過調(diào)節(jié)燃燒組分來控制試驗溫度，試驗溫度和來流速度與表1三種工況下的入口溫度和出口馬赫數(shù)保持一致. 試驗中采用K型熱電偶進行試件背風處溫度測量[12]，熱電偶安裝位置與數(shù)值模擬中的溫度監(jiān)測位置相同，如圖9(c)所示. 結(jié)構(gòu)形貌變化監(jiān)測采用DY100A型高溫氧化燒蝕測量儀，如圖9(d)所示，其測量原理是，基于高頻率相機中形貌變化過程的圖像，利用圖像分析對比技術(shù)，對實測圖像進行分析計算.

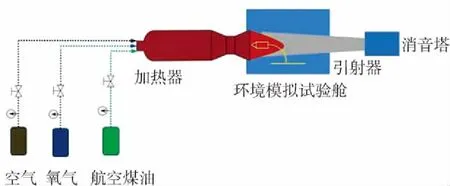
(a)風洞裝置原理圖

(b)風洞裝置實物圖

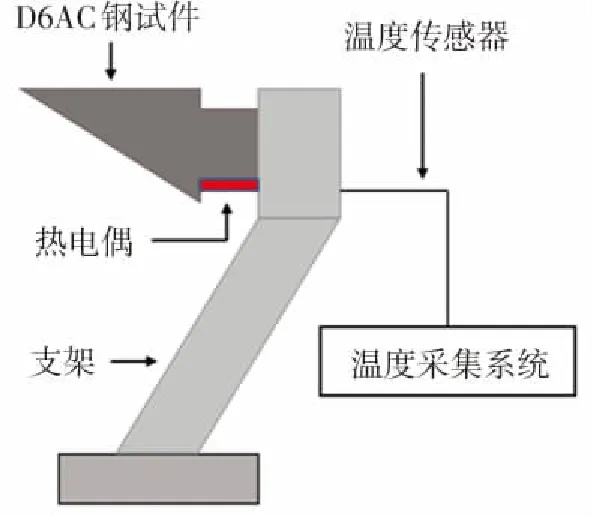
(c)熱電偶位置

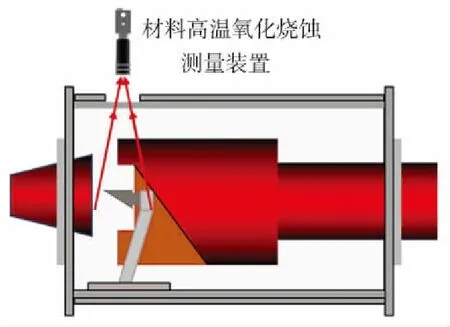
(d)材料燒蝕測量儀位置

圖10為工況1下結(jié)構(gòu)發(fā)生失效的形貌變化，可以看出，頭部兩側(cè)最先失效，因為在兩個端面產(chǎn)生的氣動熱數(shù)值最大，所以最先發(fā)生熔化，該過程與模擬結(jié)果一致.

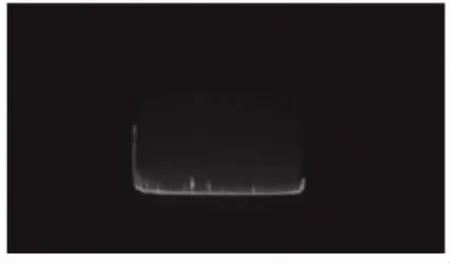
(a)燒蝕開始第0 s

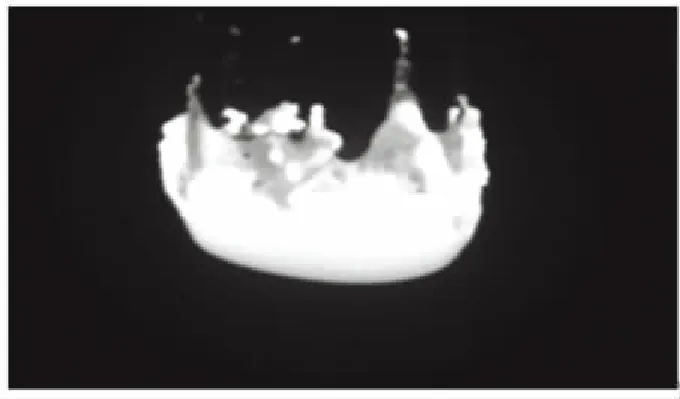
(b)燒蝕開始第2.2 s

(c)試驗前形貌

(d)試驗后形貌

風洞試驗主要模擬10 km高空的實際環(huán)境，氧氣含量極低，因此D6AC鋼失效的主要形式是相變，由資料可知，D6AC鋼熔點是1 625 K，根據(jù)熔點得到它的熔化時刻，如表4所示.

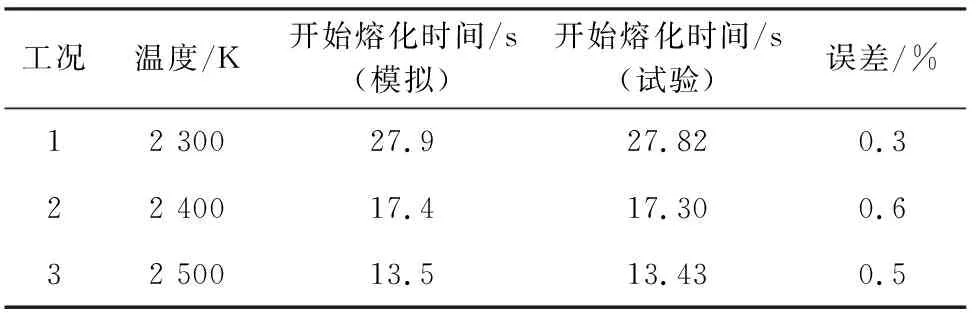
表4 D6AC鋼相變開始時間

圖11為三種來流條件下結(jié)構(gòu)燒蝕量隨時間變化的模擬結(jié)果，可以看出，來流溫度越高，開始燒蝕的時間越早. 隨著來流溫度的升高，熱流密度逐漸增大，單位時間內(nèi)熱量累積速率不斷增大，因此試件開始熔化的時間依次提前. 根據(jù)試驗數(shù)據(jù)和模擬結(jié)果可知，以D6AC鋼熔點為參考標準，達到熔點的時間與試驗時間之間的誤差分別為0.3%，0.6%，0.5%.

圖11 結(jié)構(gòu)燒蝕量隨時間的變化曲線

圖12為三種來流條件下風洞試驗與模擬的監(jiān)測點溫度對比，可以看出，二者是相匹配的，模擬的最終溫度(t=40 s)也與試驗結(jié)果吻合，三種工況下的模擬結(jié)果和試驗結(jié)果在時間歷程內(nèi)的最大誤差分別為3.13%、3.41%和2.14%. 因此，本文采用的數(shù)值模擬方法對于高超環(huán)境下熱防護材料氣動熱計算和疲勞破壞等相關(guān)試驗具有普適性和準確性.

3 熱防護材料失效影響因素分析

高超聲速環(huán)境非常復(fù)雜，導(dǎo)致材料失效的因素很多，其中飛行高度、飛行速度、飛行迎角和飛行器形狀的影響較為顯著. 運用之前證明過的耦合計算方法和D6AC鋼尺寸模型，可以探究出不同高度、速度、迎角以及不同飛行器形狀下氣動熱的數(shù)值大小.

3.1 飛行速度對熱防護材料的影響

由于不同飛行速度會使結(jié)構(gòu)頭部對其前緣的空氣產(chǎn)生不同的壓縮效果，導(dǎo)致區(qū)域溫度和熱流分布情況不同，進而影響到結(jié)構(gòu)內(nèi)部的傳熱及變形情況，所以有必要分析不同速度下熱防護材料的氣動加熱和結(jié)構(gòu)響應(yīng)過程. 結(jié)構(gòu)材料為D6AC鋼，根據(jù)實際環(huán)境，以飛行高度20 km，迎角0°為初始條件，分別研究4Ma、5Ma、6Ma下結(jié)構(gòu)溫度隨時間的變化，最大溫度值如表5所示，結(jié)構(gòu)前緣溫度隨時間變化曲線如圖13所示. 可以看出，隨著馬赫數(shù)的增大，結(jié)構(gòu)前緣駐點的溫度也逐漸增大，但不同速度下，結(jié)構(gòu)前緣的溫度趨勢是一致的，這將有利于預(yù)估更高馬赫數(shù)下的氣動加熱.

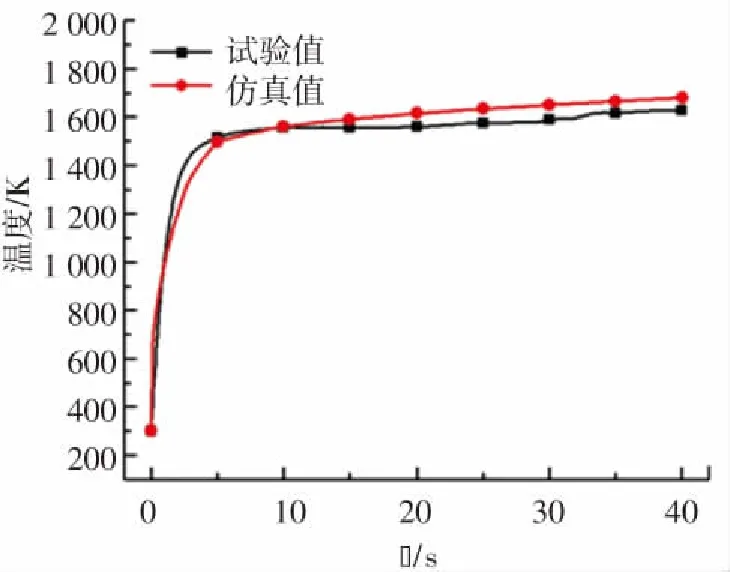
(a)工況1

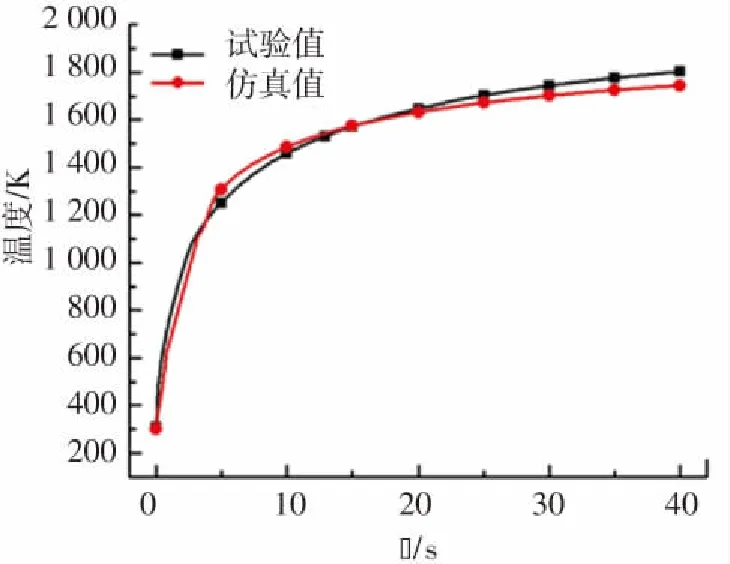
(b)工況2

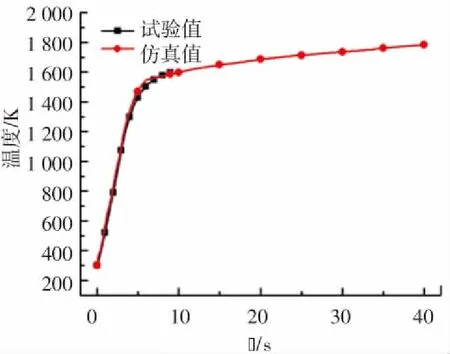
(c)工況3

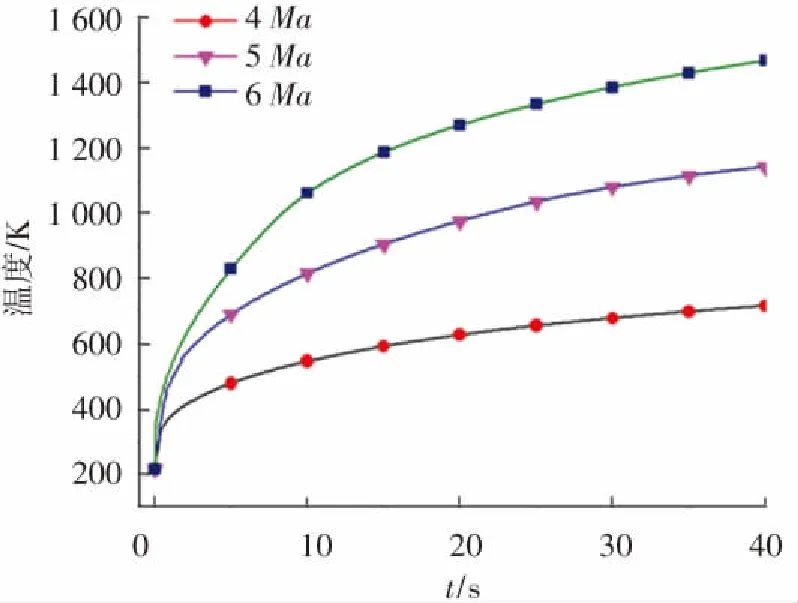
圖13 不同馬赫數(shù)下結(jié)構(gòu)前緣溫度變化曲線

表5 不同速度條件溫度最大值

3.2 飛行高度對熱防護材料的影響

由于飛行器與目標之間的距離會產(chǎn)生變化，飛行高度也會進行調(diào)整. 不同海拔高度下大氣密度、溫度等參數(shù)會有所不同，具體數(shù)據(jù)如表6所示. 以表6參數(shù)為邊界條件，飛行馬赫數(shù)為5，迎角為0°，最大溫度如表7所示，溫度隨時間變化曲線如圖14所示. 可以看出，在飛行速度，迎角一致的情況下，15～35 km海拔范圍內(nèi)，隨著高度的增加，結(jié)構(gòu)最大溫度逐漸降低. 主要原因是，隨著高度增加，大氣壓強和密度逐漸減小，氣流壓縮和摩擦作用減小，氣動加熱作用減小，熱量減小，致使結(jié)構(gòu)溫度和變形量都減小.

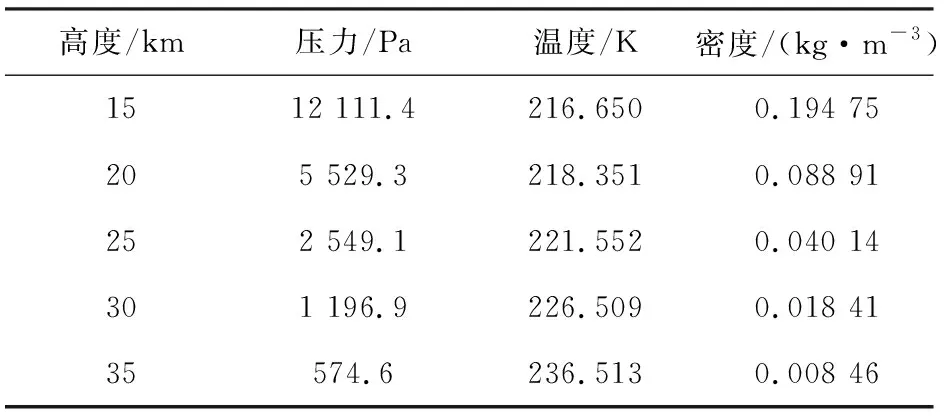
表6 不同海拔大氣屬性

表7 不同高度條件溫度最大值

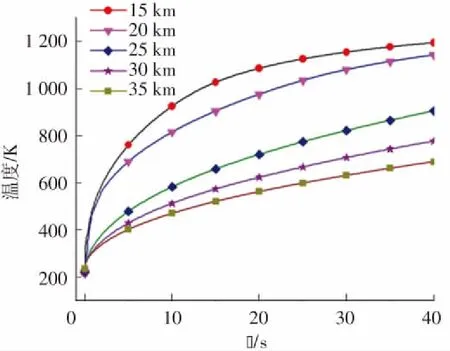
圖14 不同飛行高度前緣溫度變化曲線

3.3 飛行迎角對熱防護材料的影響

實際飛行中，飛行迎角會隨著飛行姿態(tài)的改變而產(chǎn)生變化. 迎角不同，將引起溫度、壓強等參數(shù)的改變，激波形狀和位置也會受到影響. 根據(jù)飛行特點，本文選擇-10°、-5°、0°、5°、10°五種狀態(tài)，分析飛行迎角對熱防護結(jié)構(gòu)影響，其中飛行高度20 km，飛行速度5Ma，以此得到最大溫度值如表8所示，結(jié)構(gòu)前緣溫度隨時間的變化曲線如圖15所示. 可以看出，隨耦合時間的增加，結(jié)構(gòu)前緣溫度逐漸增加，針對本文所研究的尺寸結(jié)構(gòu)，迎角為正時的結(jié)構(gòu)溫度要高于迎角為負時的結(jié)構(gòu)溫度，按照迎角由負到正的順序，隨著迎角的增大，結(jié)構(gòu)的溫度逐漸增加.

表8 不同迎角條件溫度最大值

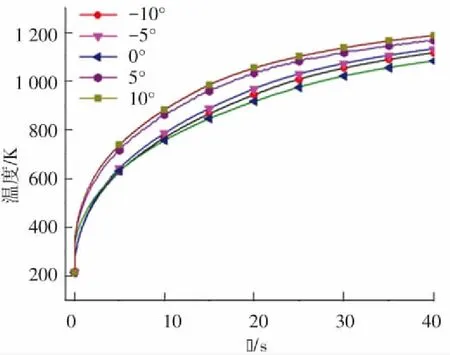
圖15 不同飛行迎角前緣溫度變化曲線

3.4 飛行器形狀對熱防護材料的影響

高馬赫數(shù)環(huán)境飛行時存在著薄激波層和熵層，而不同飛行器形狀會對激波層的形態(tài)和熵層產(chǎn)生影響，從而改變氣動熱數(shù)值大小. 為對比不同結(jié)構(gòu)形狀對氣動熱的影響，本文考慮球頭與平頭兩種形狀，保持流體域尺寸和邊界條件一致，分別采用長為37 mm，球頭半徑為7 mm的球頭模型和長為37 mm的平頭模型，飛行高度20 km，飛行速度5Ma，迎角為0°，得到最大溫度值如表9所示，結(jié)構(gòu)前緣溫度隨時間變化的曲線如圖16所示. 可以看出，在相同馬赫數(shù)下，結(jié)構(gòu)前緣溫度隨耦合時間的增加而增大，且平頭模型的最高溫度大于球頭模型. 主要原因在于，球頭模型激波與固體表面的距離大于平頭模型，導(dǎo)致激波傳熱的耗散率高，傳導(dǎo)至固體表面的熱量少，而平頭模型激波與固體表面距離小，氣動熱效果更劇烈.

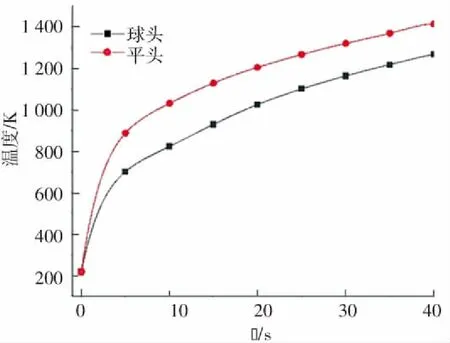
圖16 不同飛行器形狀前緣溫度變化曲線

4 結(jié) 論

1)通過多物理場耦合數(shù)值模擬，分析了來流溫度對D6AC鋼結(jié)構(gòu)氣動加熱和結(jié)構(gòu)響應(yīng)的影響，結(jié)果表明D6AC鋼在服役狀態(tài)下，前緣溫度最高，最易發(fā)生失效；來流總溫越高，服役時間越短.

2)進行了地面風洞試驗， D6AC鋼相變開始時間和監(jiān)測點溫度變化與數(shù)值模擬相吻合，證明了本文采用的多物理場研究方法在高超聲速環(huán)境下熱流固耦合方法的適用性與準確性.

3)根據(jù)多物理場研究方法對其他影響氣動熱的因素進行深入探究，模擬了不同飛行速度、飛行高度、飛行迎角以及飛行器形狀下氣動熱數(shù)值的大小. 研究發(fā)現(xiàn)，隨著馬赫數(shù)的升高，結(jié)構(gòu)前緣溫度逐漸升高；飛行海拔高度增加，空氣稀薄，氣動熱減少；根據(jù)本文采用的D6AC模型，迎角為負時結(jié)構(gòu)前緣表面的高溫區(qū)逐漸變小；相同馬赫數(shù)下，平頭模型較球頭模型的氣動熱效果更為顯著.