基于卷積神經網絡的電子音樂辨識模型

胡淑娟

(仙桃職業學院 教育學院, 湖北 仙桃 433000)

0 引言

網絡技術的快速發展令互聯網中產生大量視頻與音頻等多媒體數據[1]，電子音樂為網絡上最為普遍的多媒體音頻。電子音樂辨識作為音樂信號處理的核心問題之一，在歌曲識別、音頻匹配與推薦等方面均具有關鍵作用。針對網絡數據的海量性特性，研究一種可在海量音頻中準確快速地獲取感興趣的電子音樂是當前音頻識別領域中的熱點研究問題。

文獻[2]提出一種雙向卷積神經網絡的音樂識別模型。該模型構建雙向卷積神經網絡結構，提取音樂細節特征，將細節特征合并成一維特征向量。但該模型無法去除電子音樂內的噪聲含量。文獻[3]提出一種直接利用視音頻特征進行識別的算法，該算法融合BoW、GIST、顏色矩特征、顏色直方圖和音頻特征進行識別，但該方法無法分辨電子音樂類型，辨識精度較低。

針對當前普遍使用的音頻辨識變模型無法分辨電子音樂類型，辨識精度較低等難題，設計基于卷積神經網絡的電子音樂辨識模型，并通過實驗驗證該模型的實際應用性能。

1 基于卷積神經網絡的電子音樂辨識模型

1.1 電子音樂信號預處理

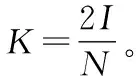
依照信號理論能夠得到[6]，電子音樂信號的諧波成分在諧波矩陣A上僅分布在分散的數個頻率成分上，同時在時間尺度上電子音樂存在顯著的重復性，由此得到矩陣A存在內在的低秩特征，也就是電子音樂和弦波信息分布在低維子空間內[7]。電子音樂非諧波成分E矩陣內聚集各種不同類型噪聲，由于不同類型造成變化的頻繁性存在一定稀疏特性[8]，基于此可利用秩函數構建諧波成分模型，利用零范數構建稀疏噪聲模型。由此可將灰度低秩矩陣定義為一個雙目標優化問題，描述為式(1)。

(1)

在式(1)內引入大于零的折中因子λ，由此以單目標優化問題替代式(1)所示的雙目標優化問題,如式(2)。

(2)

式中，多描述的優化問題實質上是1種多項式復雜程度的非確定性問題，基于此，需確定合適的可取代秩函數與零范數的函數。以確保優化問題整體具有全局最優解為目的[9]，要求確定取代函數為原函數凸包絡。而矩陣的核范數表示矩陣內全部奇異值相加的結果，可理解為是矩陣秩函數的凸包絡，矩陣內非零元素相加的結果可利用矩陣的1范數表示，一般情況下可經其作為矩陣的稀疏算子，即0范數的凸包。基于此可將式(2)所示的單目標優化問題轉化為式(3)所示的凸優化問題。

(3)

式(3)所示的凸優化問題可通過增廣拉格朗日乘子法解決，由此能夠獲取最優解電子音樂諧波信息矩陣A，其為電子音樂原始信號頻譜重建后的諧波頻譜。重建后的諧波頻譜內可分離稀疏噪聲，并重建了頻譜的低秩信息，由此可知，頻譜矩陣A內具有一定魯棒性。將去除噪聲后的電子音樂文件制作成波形圖，利用卷積神經網絡實現電子音樂辨識。

1.2 基于卷積神經網絡的辨識模型構建

1.2.1 典型卷積神經網絡

輸入層、卷積層、下采樣層、全連接層標和輸出層共同組成標準卷積神經網絡[10]。

卷積層與下采樣層結合是卷積神經網絡提取目標特征的主要結構[11]，將去除噪聲后的電子音樂頻譜波形圖作為輸入層輸入信息，可用T表示。以Xi表示卷積神經網絡第i層的特征(X0=T)。在Xi為卷積層的條件下，描述為式(4)。

Xi=f(Xi-1*Ki+bi)

(4)

式中，Ki和bi分別表示可訓練的卷積核和偏置量；*和f(x)分別表示卷積運算和激活函數。

使用較為普遍的激活函數有sigmoid函數、tanb函數以及ReLu函數等[12]。綜合考慮不同激活函數性能，選取ReLu函數作為卷積層激活函數，描述為式(5)。

f(x)=max(0,x)

(5)

ReLu函數的主要優勢主要體現在其可令卷積神經網絡部分神經元輸出為0，由此令卷積神經網絡產生稀疏選性，降低計算過程的復雜性；同時ReLu函數可顯著提升卷積神經網絡的分類能力，降低參數間的依賴性，在一定程度上改善卷積神經網絡過擬合問題；ReLu函數的導數僅為1或0，可改善卷積神經網絡誤差反向傳播過程中的梯度消失問題。

下采樣層對卷積層獲取的各特征圖內n×n區域的像素實施采樣處理，降低特征圖尺寸。普遍使用的采樣處理過程可分為上限值采樣與均值采樣[13]。在Xi表示下采樣層的條件下，上限值采樣與均值采樣表示為式(6)、式(7)。

Xi=f(WiPmax(Xi-1)+bi)

(6)

Xi=f(WiPmean(Xi-1)+bi)

(7)

式中，Pmax(x)和Pmean(x)分別表示上限值采樣操作和均值采樣操作;Wi和bi分別表示取值與偏置值。

下采樣層的主要功能是以保留原始特征信息為基礎，進行特征圖降維處理，防止出現維數災難，提升變形魯棒性；同時利用下采樣層還可壓縮特征圖，令計算過程難度下降。

通常情況下，全連接層處于卷積層、下采樣層同輸出層之間，可將其定義為一個同淺層神經網絡功能相似的多層感知機，其主要功能是將分布式特征表示映射至樣本標記空間內，并在卷積神經網絡模型表示能力遷移過程中發揮防火墻功能[14]。

輸出層為一個解決多分類問題的分類器，采用由Logistic回歸模型在多分類問題方面演化處的Soft Max分類器。考慮Logistic函數僅可實現二分類功能，因此Soft Max分類器在繼承Logistic函數回歸的基礎上，通過多項Logistic回歸完成多分類任務。用y表示Logistic回歸內的多分類標簽，其取值范圍為不小于2，訓練樣本集合為k個被標簽的樣本，描述為式(8)。

T={(x1,y1),(x2,y2),…,(xk,yk)}

(8)

式中，yi∈{1,2,…,k}和xi分別表示分類標簽與樣本集合。

j表示不同電子音樂類型，判斷j的概率值，表示單個電子音樂頻譜波形圖歸為第k類標簽概率的表達式為式(9)。

P(y=j|x)(j=1,2,…,k)

(9)

式中，能夠表示回歸樣本集合轉換為k維度的概率向量，概率向量的函數為式(10)。

(10)

(11)

式中，1{yi=j}表示若yi=j，則兩者均為1，相反兩者均為0。損失函數迭代次數的提升可優化Soft Max分類器參數[15-16]，提升參數準確定，實現不同電子音樂頻譜波形圖樣本的準確辨識。

1.2.2 卷積神經網絡優化

標準卷積神經網絡對圖像進行一層層的映射，直至最后只將輸出層作為特征提取結果[17-18]，這一過程中在中間層丟失大量關鍵圖像特征，降低辨識精度。針對這一問題，結合層間特征融合思想，在輸出層輸出特征提取結果過程中輸出輸入圖像在卷積神經網絡內每一層的映射結果，選取主成分分析法對提取的全體輸出特征實施降維處理，將其融合為多層深度特征。同時，在下采樣過程中將上限值采樣與均值采樣相結合，即利用混合采樣的方式充實采樣層的多樣性。利用混合采樣模式能夠同時得到上限值采樣與均值采樣獲取的特征值[19-20]，得到更為豐富的圖像，提升卷積神經網絡辨識的穩定性，混合采樣模式的表達式為式(12)、式(13)。

(12)

Xi=f(WiTi+bi)

(13)

基于特征提取方式的優化能夠改善標準卷積神經網絡中單一輸出層與采樣層特征提取不全面的問題，可充分提取電子音樂頻譜波形圖的特征并實現特征融合，提升卷積神經網絡辨識性能。

利用反向傳播算法進行卷積神經網絡訓練，卷積神經網絡經由正向計算與反向傳播過程，持續優化權值與閾值，令自身均方誤差函數持續下降，以滿足卷積神經網絡訓練需求。

2 實驗結果與分析

實驗為測試本文設計的基于卷積神經網絡的電子音樂辨識模型對于電子音樂辨識的性能，選取國際音頻檢測賽事中所有數據的音頻數據集為實驗對象，其中包含220首電子音樂(采樣率與比特率分別為10 080 Hz和16 bits)。將實驗對象內全部電子音樂手動標記的標簽文件作為實際標簽文件，將這些標簽文件作為測試數據的生成依據以及本文模型電子音樂辨識結果的對比依據。

2.1 電子音樂預處理效果測試

利用本文模型對實驗對象內的電子音樂進行預處理，研究對象中編號為22號的電子音樂預處理結果如圖1所示。

分析圖1得到，采用本文模型對研究對象進行預處理后，研究對象頻譜波動更為平滑，這是由于本文模型中重建研究對象信號頻譜內諧波信息，去除研究對象信號頻譜內的噪聲，對去噪后的研究對象進行辨識，可提升本文模型辨識結果。

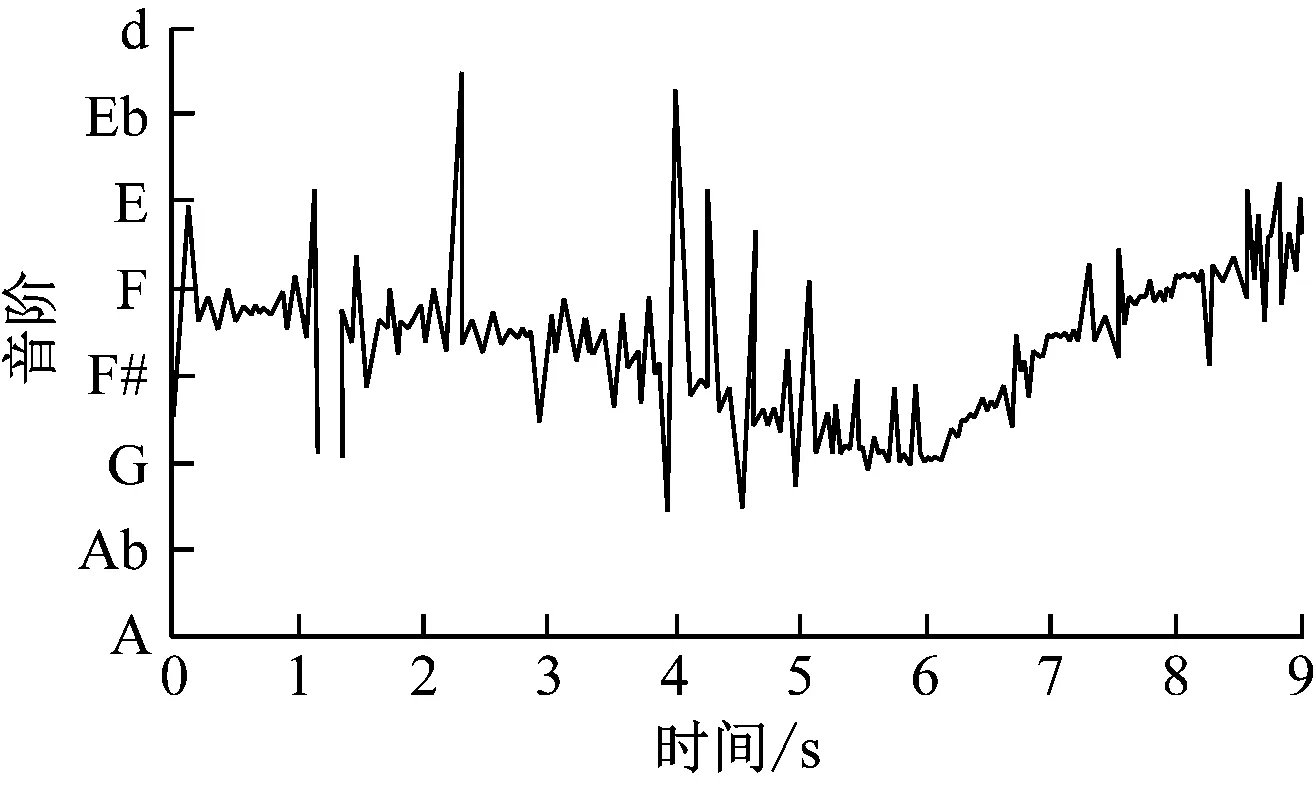
(a) 預處理前

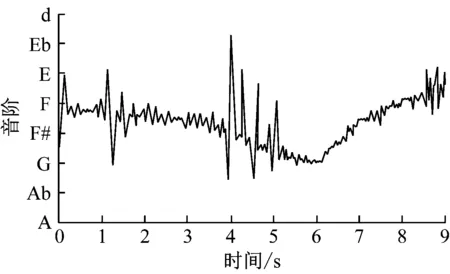
(b) 預處理后圖1 研究對象預處理結果

2.2 模型訓練過程測試

將研究對象內全部220首電子音樂分為兩部分，分別定義為訓練樣本集和測試樣本集，各樣本集內電子音樂數量分別為160首和60首。在本文模型中輸入訓練樣本集進行訓練，本文模型訓練過程如圖2所示。

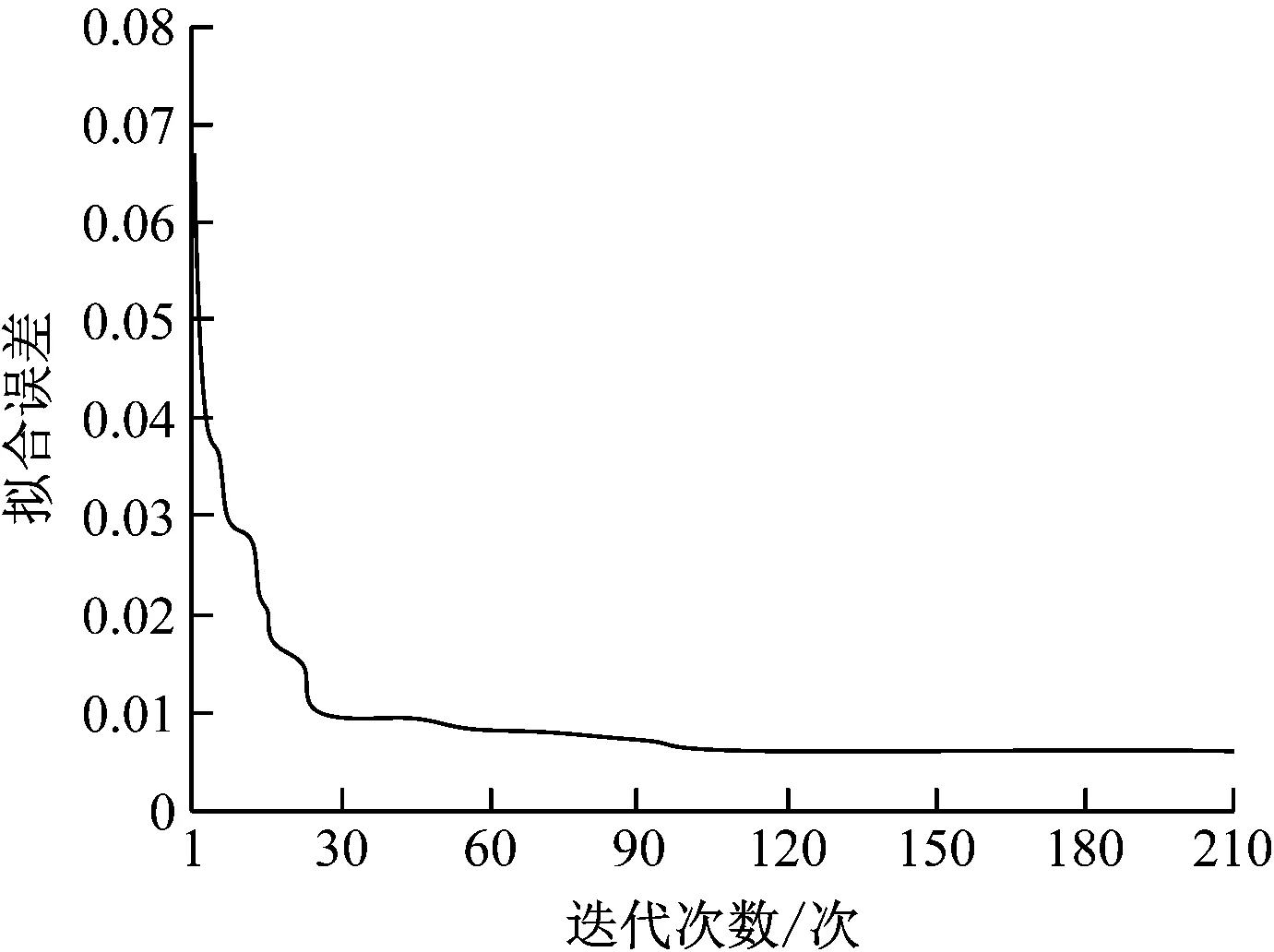
圖2 模型訓練過程

分析圖2得到采用本文模型辨識研究對像過程中，卷積神經網絡初次迭代時，本文模型擬合誤差為0.067。隨著本文模型迭代次數逐漸上升，本文模型的擬合誤差呈逐漸下降狀態。本文模型迭代次數提升至30次時，本文模型的擬合誤差下降至0.01。在本文模型迭代次數上升至100次時，本文模型的擬合誤差下降至0.008。隨著本文模型迭代次數持續上升，本文模型的擬合誤差保持在0.008，由此說明本文模型具有較快的訓練效率，即本文模型具有較快的辨識效率。同時由圖2可知，隨著本文模型迭代次數逐漸上升，本文模型的擬合誤差呈逐漸下降狀態，擬合誤差越小，表明擬合精度越高。這是因為利用Soft Max分類器優化迭代過程，使得損失函數迭代次數的提升可優化Soft Max分類器參數，進一步提升參數準確率。且ReLu函數可顯著提升卷積神經網絡的分類能力，降低參數間的依賴性，在一定程度上改善卷積神經網絡過擬合問題，迭代次數的提升可進一步提升擬合精度。

2.3 不同方法下識別結果

為驗證本文模型的有效性，將文獻[2]模型和文獻[3]模型作為對比對象，不同方法辨識結果如圖3所示。

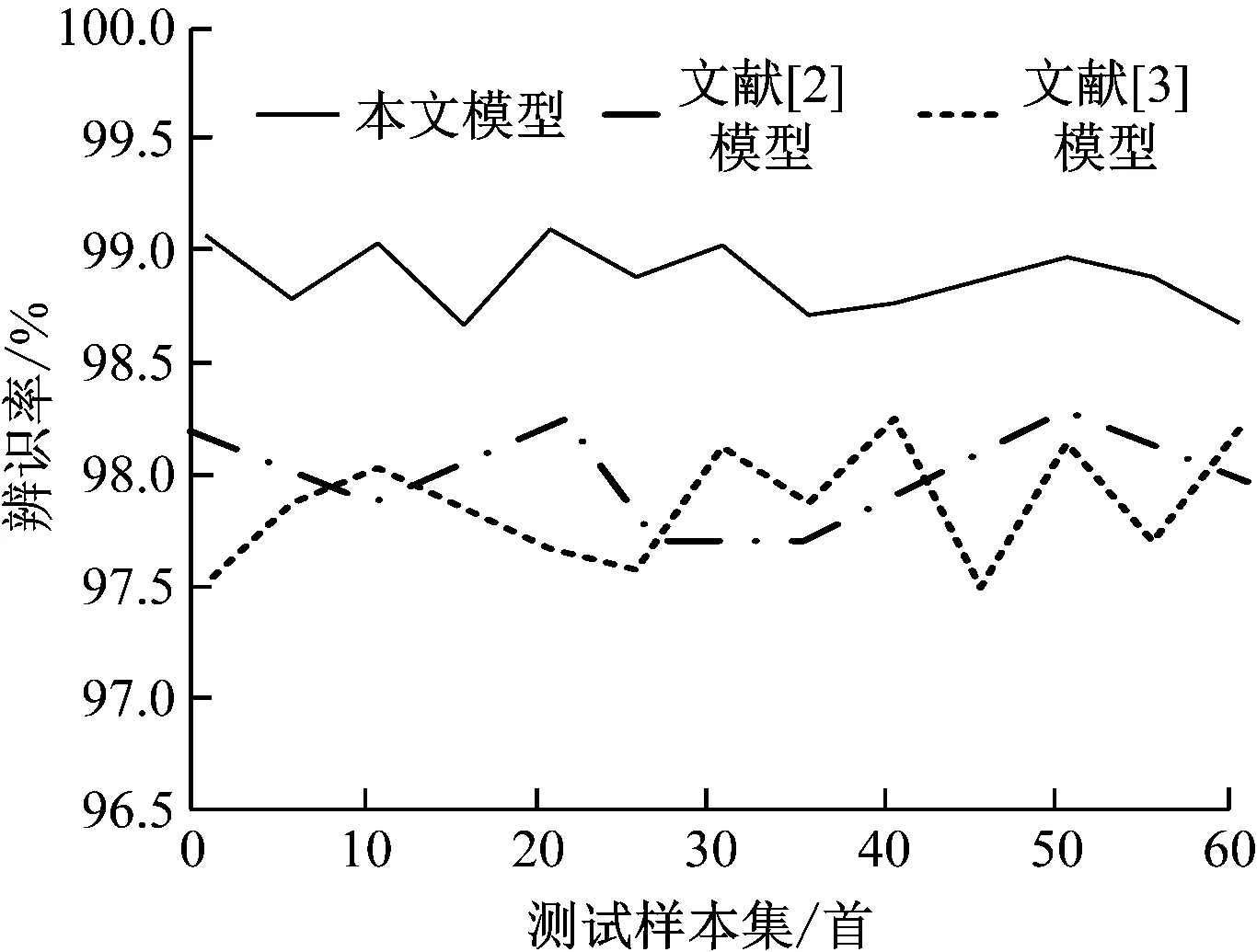
圖3 不同模型辨識結果

分析圖3得到，相比文獻[2]模型和文獻[3]模型，本文模型對測試樣本集內各測試樣本進行辨識，所得辨識率均高于98.5%，由此說明本文模型能夠準確辨識測試樣本，具有較高的辨識率。

2.4 模型采樣方式對辨識率的影響

為研究模型下采樣層不同采樣方式對模型辨識率的影響，在本文模型其他條件完全一致的條件下，對比下采樣層采用上限值采樣、均值采樣和混合采樣時本文模型的辨識率如圖4所示。

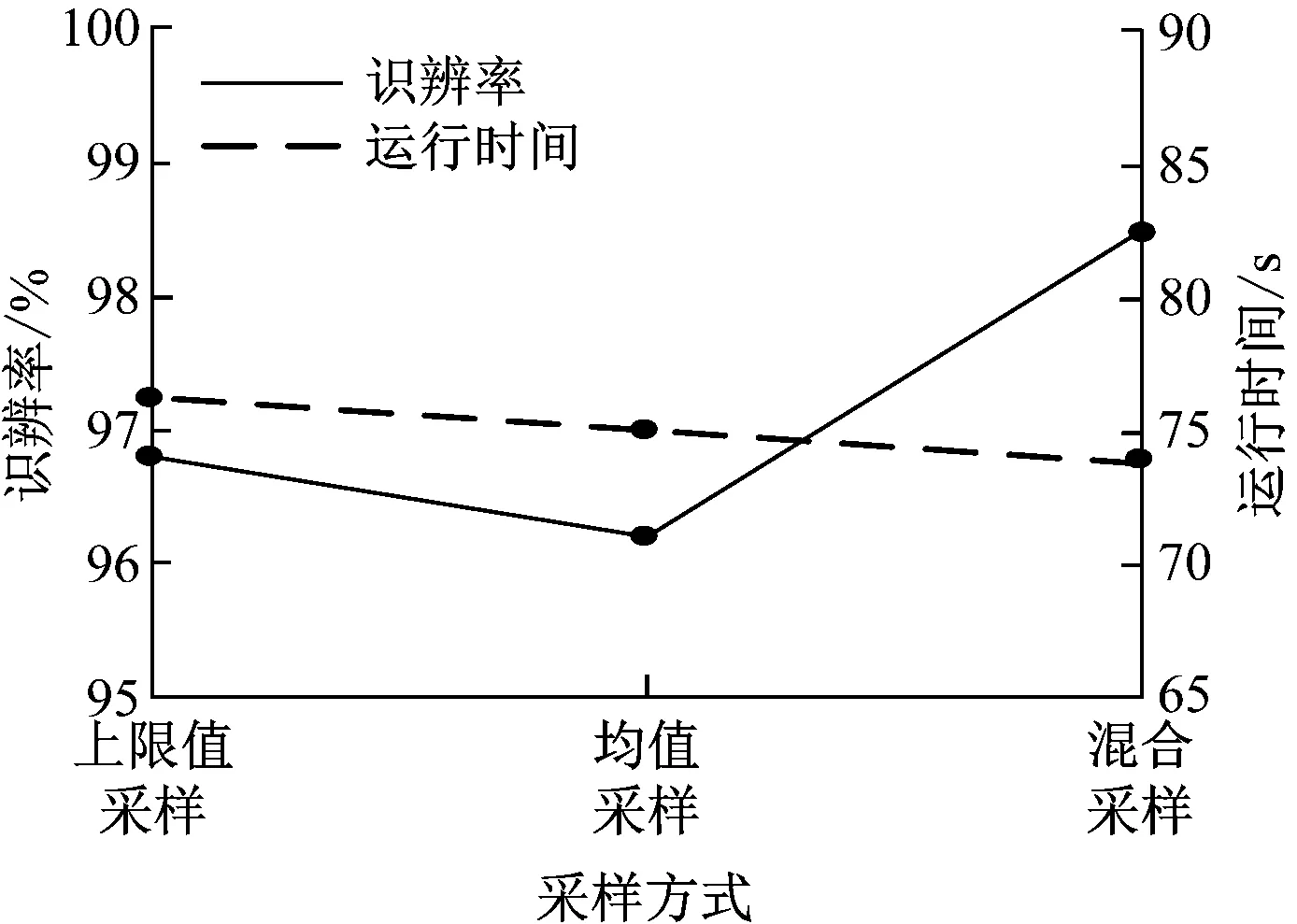
圖4 不同采樣方式下模型的辨識率

分析圖4，本文模型采用上限值采樣方法、均值采樣方式和混合采樣方式進行研究對象辨識的運行時間差距較小，低于2 s。說明不同采樣方式對本文模型的辨識效率的影響并不顯著。但本文模型采用混合采樣方式進行辨識的辨識率均值達到98.5%，顯著高于采用上限值采樣與均值采樣時的辨識率。由此說明混合采樣方式可提升本文模型辨識率。

3 總結

本文設計基于卷積神經網絡的電子音樂辨識模型，在電子音樂信息預處理后，利用優化后的卷積神經網絡辨識電子音樂。實驗結果顯示本文模型能夠準確辨識電子音樂，且具有較快的效率。在后續優化過程中主要針對如何利用多尺度池化的理念進一步優化卷積神經網絡，令本文模型在保障辨識精度與效率的基礎上，能夠接受任意尺寸的輸入圖像。