保險資產證券化及互助保險穩定性分析模型

葛聯迎

(西安歐亞學院 金融學院, 陜西 西安 710065)

0 引言

互助保險[1](Mutual Insurance，MI)自問世以來，因其靈活、民主等特點，在社會保障體系中占重要地位，發揮著社會保險和商業保險不可替代的作用。互助保險相對于商業保險具有獨特優勢[2-3]，如保留作為被保險人財產的資金、更廣泛的風險管理能力等。這種保險機制在一定程度上能夠減輕國家預算中與賠償人為和自然災害造成的損害、自然壟斷損失有關的財政負擔，并帶來積極的社會回報，如減少民事責任風險、加強社會保護、提高環境保護質量等。然而，初始階段的MI的穩定性損失風險較高，究其原因主要是由于積累的資金不足以支付不良事件造成的損失[4]。在經濟形勢不穩定的時期，這些風險顯著增加。

為改善這類情況，可以通過使用保險資產證券化[5-6]機制，確保可靠的風險覆蓋率，以不高于商業保險公司的價格平價，并在可能的情況下不使各方負擔過重，從而加強其活動初始階段的MI穩定性。此外，獨立且經濟上獨立的法律實體通常充當基金再保險人，即特殊目的機構[7](Special Purpose Vehicle，SPV)。為此，國內外眾多學者對此進行了研究，并取得了豐碩成果。范陽等[8]從市場發展、監管規則、法律、稅收與會計、操作實踐、投資者情況等方面對澳大利亞證券化市場的發展進行系統的介紹，并對照我國的具體情況，提出促進我國資產證券化市場發展的幾點建議。張祖榮[9]在對分析保險資金的負債性、返還性和社會性等特點決定了保險資金運用受安全性、流動性和收益性等條件約束的基礎上，研究了保險資金運用的策略選擇。

然而，互助保險的資產證券化對其金融穩定水平的影響在實踐中是很難評估的，因為這種業務產生的資金流與MI基金積累和支出的傳統過程(收到供款、將其資金投放金融市場的收入和保險費)。在這種情況下，分析方法可能無法產生預期的結果。為了解決這一問題，本文采用模擬方法，在其結構內模擬MI基金的積累和支出過程，同時考慮到保險支付隨機流動的時空分布。這些方法可以通過模擬建模過程中獲得的樣本，根據資產證券化參數來評估互助保險的穩定性特征。

1 方法

1.1 模型建立

MI基金在某個時期[0,T]積累資金的過程可以表示為一個時間序列{Ht}，t∈[0,T]，其值是在考慮資金流入和流出的情況下形成的。接下來引入以下假設來簡化模型。

(1) 參與者數量、MI保險組合以及收到的保險費金額隨著時間的推移保持不變；

(2) 每年年底所有付款后剩余的資金以固定收益率i0(%)投放金融市場，即為無風險利率；

(3) MI開展自身活動的費用可以忽略不計。

因此，第t年MI保險基金的數量變化ΔHt可以表示為式(1)。

ΔHt=Ht-Ht-1=i0Ht-1+r-Qt

(1)

其中，i0Ht-1等式右邊為上期累計投入MI基金取得的投資收益；r為MI當年收到的保險費總額；Qt為第t年的保險費總額。

進一步，令時間t=0時的保險資金量為H0，則第t年MI保險基金的資金量遞推公式為式(2)。

(2)

1.2 資產證券化對MI的影響

假設從t年內的時間點t=0開始，保險人對MI的部分義務分配到[0,T]期間，本文將這部分金額定義為未來保險費r。按照此模式不斷積累，第t年MI保險基金的數量變化ΔHt可以更新如式(3)。

ΔHt=Ht-Ht-1=i0Ht-1+(1-α)r-Qt

(3)

由于采用了證券化機制，在研究期初，MI基金的數量將隨著出售特殊目的機構債券所得收益S減去構建交易C的成本而增長，因此為式(4)。

H0=H0+S-C

(4)

顯然，S的值取決于α的值。這種依賴的程度可以確定如下。假設SPV發行的債券按票面利率i1(%)出售，票面利率在T年內每年支付一次，而名義回報率在上一年一次性支付。另外，假設SPV基金的剩余部分是以零風險利率i0存放，則第t年SPV資產量W的變化可表示為式(5)。

ΔWt=Wt-Wt-1=αr-i1S+i0Wt-1

(5)

其中，αr為本年度保險合同的付款流入金額；i1S為已發行債券的息票付款；i0Wt-1第三個總和為SPV賬戶余額的收益率。

在T年，息票的付款必須加上票面價值付款，考慮到這一點，式(5)可進一步更新為式(6)。

ΔWT=WT-WT-1=αr-i1S-S+i0WT-1

(6)

將債券發行成本歸因于MI的成本，本文將新成立的SPV的初始資金額設為W0=0。接著，根據遞推式(5)和式(6)，可以得到式(7)，描述在完成對保稅貸款的所有付款后形成的SPV余額。

(7)

在時間T時，SPV停止運行。因此，當假設保險費保持不變，式(7)可轉換為式(8)。

(8)

為簡化計算，引入符號k，則有式(9)。

(9)

進一步，在式(8)中求解S，則后續溢價和已發行債券的數量相關比率表示如式(10)。

(10)

接下來，假設證券化交易的成本由固定成本和可變成本組成，則其與證券化資產的數量成比例可表示如式(11)。

C=c0+c1αr

(11)

結合式(4)、式(10)和式(11)，進一步將得到MI基金的初始規模可以表示為式(12)。

(12)

結合初始條件式(12)與式(3)，進一步將得到考慮序列化的MI資金積累過程，如式(13)。

(13)

2 MI交易過程及其穩定性模型

2.1 MI交易過程

本節將詳細介紹保險資產證券化交易MI過程。

發行人將其出資的一部分出售給新成立的SPV，獲得的金額等于購買價格減去交易結構成本。SPV通過發行證券-保險債券為購買價格融資，由于SPV不擁有任何資產，而且擁有最低資本，該法人實體本身無法進入資本市場。因此，本交易建議其擔保人提供額外擔保。特別是公共機構可以作為其擔保人。投資者購買由特殊目的公司發行的債券，以證明對該公司債券的索賠權。與政府貸款風險相比，這些證券的風險微不足道，但盈利能力卻超過了它們，這一切都決定了金融市場對這些證券有相當高的需求水平。因此，資產證券化允許MI增加自己的資金，從而加強其財務穩定性，特別是在該交易實施后的第一個時期。

在這種情況下，未來支付利息和本金通常已經無法實質性地惡化MI的財務狀況，因為這些財務資源的外流在很大程度上是由MI成員每年的保險繳款財政收入和安置可得保險資產的可能收入來補償的金融市場MI的資金。

2.2 MI穩定性建模

本節的目的是建立依賴關系，即將MI基金的穩定指標水平與其資產價值α受序列化影響的份額聯系起來。將在T年的有限時間間隔內使用其違約概率P作為MI穩定性指標，如式(14)。

P=Pr{?t≤T:Ht<0}

(14)

同時，在該時間間隔的第t年內，基金違約的概率Pt定義如式(13)，且有t=1,2,…,T-1。

Pt=Pr{Ht<0|Ht-1≥0}

(15)

本文將計算每個過程實現樣本(式(13))的這些概率的估計值，從而作為樣本中存在不等式的實現數與它們的總數的比率。在這種情況下，各種實施樣本的參數值將有所不同，且會影響證券化的MI資產份額，并影響其資金H0的初始量(式(12))。α值從集合0≤α≤α*中選擇，其中α*是該指示符的上限，且不超過1。

為簡化計算，本文在接收到每個樣本后的假設如下。

1) 在[0,T]年時間間隔內MI運行模式的下列參數的值是恒定的：H0是由其成員形成的MI基金的數量；r為保險費水平；i0為無風險利率；c0和c1為構建證券化交易的固定和可變成本；i1為已發行債券的票面利率；T為其償還期。

2)t年的MI保險賠付服從復合泊松分布，即MI基金一年的賠付次數由泊松隨機變量N和參數λ確定，同時支付的數量qn是密度pq(x)和分布參數∧的指數分布隨機變量，如式(16)。

(16)

pq(x)=∧e-∧x

x≥0

MI向社會每個成員收取的年度供款(保險費)的規模估算式為式(17)。

r=(1+ξ)E[Q]

(17)

其中，系數ξ描述MI風險負荷。

3 實驗與分析

實驗的量級為106，且每個α值以0.01的增率在0到1的范圍內變化。實驗所用相關參數如表1所示。

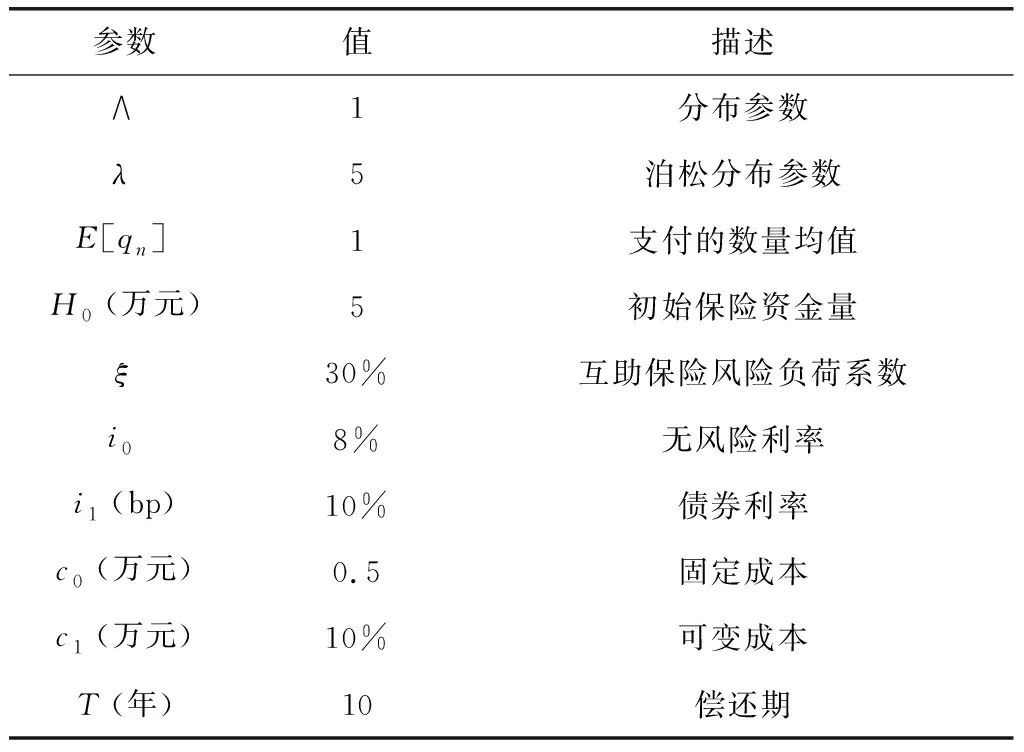
表1 實驗相關參數選取

初始容量H0=5，風險溢價為10%的MI基金違約率變化情況如圖1所示。

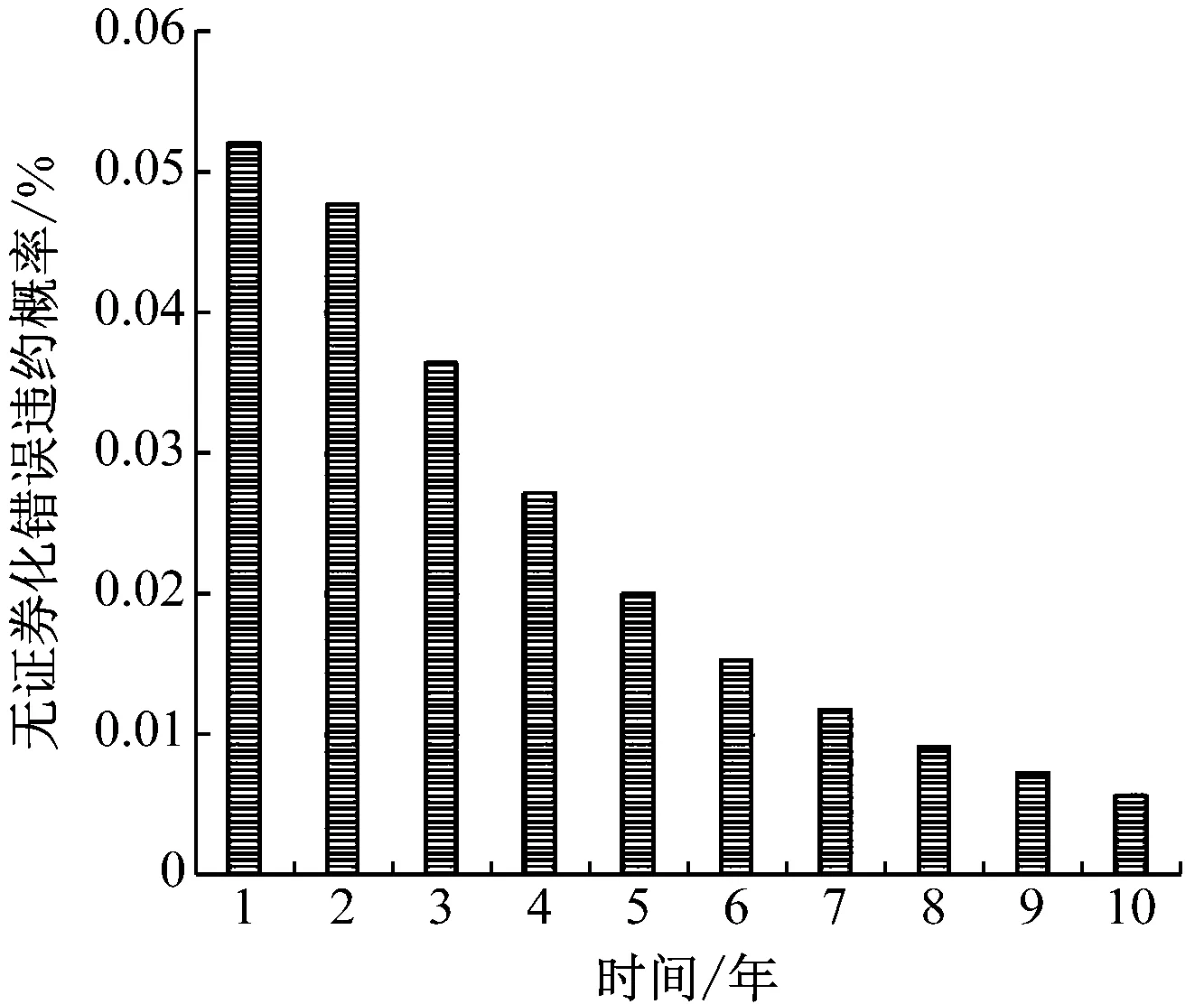
圖1 無證券化MI基金違約率變化情況

可以看出，隨著時間的推移，基金違約的年概率值迅速降低，但在誤操作的最初幾年，它們的水平相對顯著。

使用證券化機制可以使這種關系的性質發生重大變化，如圖2所示。

在第一年進行債券發行后，由于納入了從金融市場募集的資金，基金的穩定性顯著提高(年度違約概率降低)。同時，由于保險費不足，違約概率在隨后的幾年中先有所增加，然后開始下降。在這種情況下，這一指標的價值大約在第5年之前不會超過在沒有證券化的情況下獲得的相應水平，并且在隨后的一段時期(從5年到10年)已經超過這些水平。概率Pt變化的性質在很大程度上取決于參數水平α。這允許在一定程度上調整MI基金穩定性，可以用于制定其發展戰略，以滿足成員或監管機構設定的金融穩定的門檻要求。

4 總結

MI在社會保障體系中占重要地位，發揮著社會保險和商業保險不可替代的作用。在經濟形勢不穩定的時期，MI的穩定性損失風險較高。這種問題可通過保險資產證券化機制得到改善。

然而，由于業務產生的資金流與MI基金積累和支出的傳統過程存在的復雜特效，互助保險的資產證券化對其金融穩定水平的影響在實踐中是很難評估的。為此，本文模擬MI基金的積累和支出過程，并利用模擬過程產生的數據，分析證券化機制對MI基金穩定性的影響。