基于改進K-means的大數據清洗方法

林女貴， 吳元林

(1.國網福建省電力有限公司， 福建 福州 350001;2.國網信通億力科技有限責任公司， 福建 福州 350001)

0 引言

隨著智能化技術的發展，海量的網絡數據被采集到各個系統，有效地利用海量數據挖掘數據中存在的價值，最關鍵的一點是提高數據質量[1-2]。目前的大數據中存在的低質量數據主要包括冗余數據、缺失數據和異常數據[3]。一直以來的研究對于冗余數據和缺失數據的處理已經比較完善，而對于大數據中異常數據的處理還處于初級階段[4]。為了提高數據質量，達到數據清洗的目的。Hadoop平臺是有效處理大數據的軟件，利用其對數據進行清洗，可以得到高質量的數據。

由于數據挖掘的效果受數據質量影響較大，所以需要對大數據進行數據清洗以提高數據利用效率。目前數據的采集量越來越大，針對大數據清洗的研究也受到了人們的廣泛關注。文獻[5]對輸變電設備的異常數據進行了分類，采用一種基于時間序列分析的雙循環迭代檢驗法，對變壓器和線路的數據進行清洗，得到了較高質量的數據。文獻[6]針對并行數據的清洗問題進行了研究，提出了基于任務合并的優化技術，對冗余計算和同一文件進行合并，降低了系統的運行時間，提高了數據清洗的效率。文獻[7]采用條件合并方法把關聯數據放在一起，提出了一種自動清洗結構，對數據進行檢測和修復，并對關聯數據的一致性和時效性進行了判斷，經過實驗對比驗證了該方法的有效性。文獻[8]針對風電機組采集的風速功率數據，采用組內方差清洗方法，對風機的發電狀況進行判斷，該方法能夠準確識別風機功率曲線并檢測出異常工作狀態。文獻[9]分析了異常負荷數據的產生原因，采用基于密度的負荷數據流異常辨識方法和基于協同過濾推薦算法的負荷修復方法，將該方法在實際負荷數據上進行實驗，驗證了該方法能夠有效提高配電網數據質量。文獻[10]采用棧式自編碼器方法，對輸變電設備正常及異常的數據進行學習，建立起缺失數據和設備異常的模型，實驗結果證明，該方法能夠有效過濾干擾數據。文獻[11]在采用大數據方法評估變壓器狀態的時候，針對數據中存在數據缺失和異常的問題，建立數據之間的關聯規則模型，采用基于密度的聚類方法檢查數據的缺失值和異常點，采用小波神經網絡對異常數據進行修復，提高清洗數據的質量。

本文針對Hadoop平臺下的大數據進行異常數據清洗的研究，以保障數據清洗的有效性。采用基于損失函數的Logsf方法對高維數據進行降維處理，采用Canopy方法對K-means進行改進，并采用改進的K-means方法對異常數據進行清洗。

1 Hadoop平臺下數據清洗方法

在對數據分析之前，會對數據進行清洗，以查找數據中存在的“低質”數據[12]。清洗過后的數據需要數據質量評價，數據質量的評價主要包含2個元素：定量元素和非電量元素。定量元素主要是從如下方面對數據清洗結果進行評價：清洗數據的完整性;清洗數據的一致性;數據的唯一性;數據的準確性;數據的有效性;數據的時間性。非定量元素主要包括數據處理的目的，數據集的用途和數據集從采集到處理的過程描述。本文采用定量元素方法評價清洗過后的質量，并采用Hadoop平臺，對處理后的數據的查全率和可擴展性進行分析。

數據清洗的過程如圖1所示。

圖1 數據清洗流程圖

原始數據是指數據倉庫中存儲的數據信息；數據預處理指的是對原始數據進行簡單的約束處理；特征選擇指的是提取數據特征，剔除冗余信息；數據清洗指的是根據實際應用情況，清洗臟數據；清洗結果檢查指的是根據清洗標準檢驗數據質量。

由于Hadoop在處理大數據上的優越性，采用Hadoop的分布式數據清洗方法，可以有效提高大數據清洗的效率。采用Hadoop方法清洗數據的時候，將數據分為存儲層和清洗計算層。采用HDFS進行數據存儲，在HDFS上層采用Hive數據倉庫實現數據的轉存，然后將數據庫的數據按照指定格式進行處理，實現數據清洗前期的準備工作。本文采用MapReduce方法實現異常數據的分布式清洗，提高數據清洗的效率和準確性。Hadoop平臺的異常數據清洗流程如圖2所示。

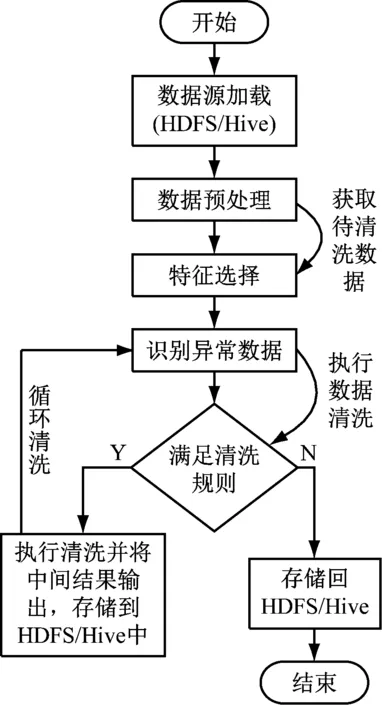
圖2 分布式異常數據清洗流程

具體的分布式數據清洗流程如下所述。

(1) 數據源加載。采用Sqoop和Hive對采集的數據進行加載和轉存。

(2) 數據預處理。根據數據需求進行綜合分析，以確保數據分析時數據的可用性。

(3) 特征選擇。選擇出影響數據質量的主要特征，剔除冗余特征，實現大數據的降維處理。

(4) 識別異常數據。采用改進的K-means算法，將距離相差越大異常性越強的數據，采用MapReduce方法實現并行化計算。

(5) 清洗結果檢驗。對清洗后的數據進行數據質量檢查，確保數據質量。

2 基于改進K-means的異常數據清洗方法

2.1 基于Logsf的特征選擇方法

Logsf可以描述為假設訓練樣本集R={M,N}={mi,ni}。其中，mi為第i個訓練樣本；ni為第i個樣本的標記[13]。每個樣本包含d維矢量，mi={mi1,mi2,mid}∈Rd。樣本mi的損失函數定義為式(1)。

L(β,mi)=log(1+exp(-βTFi))

(1)

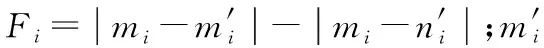
Logsf算法的評價函數可以表示為式(2)。

(2)

式中,K表示樣本特征數量；e(β)是所有特征樣本損失函數之和。如何確定最優的β′求取最小的損失函數，是需要研究的問題，本文采用梯度下降方法求取最優權重。

設步長為α，梯度下降法的迭代算式表示為式(3)。

(3)

將式(1)帶入式(3),則可得到式(4)。

(4)

簡化后可得到式(5)。

(5)

通過上述方法可以得到最優權重，但是在Logsf中存在著最鄰近思想，確定特征樣本相似度的方法為式(6)。

(6)

2.2 基于改進K-means算法的數據清洗方法

數據中存在著與主體數據不相符的數據，被稱為異常數據。K-means算法的步驟[14-15]如下所述。

從訓練樣本{x1,…,xm},xi∈Rn，隨機取k個中心點。

Step1：從{x1,…,xm}隨機取k個樣本，記作初始聚類中心μ1,μ2,…,μk∈Rn。

Step2：求取其他數據與該中心樣本的距離，數據樣本根據距離劃分類別,如式(7)。

(7)

Step3：對每個類j，求取平均值確定中心點,如式(8)。

(8)

式中，每個樣本含d個屬性，第j類共m個數據，其中樣本xi屬于第j類，屬于第j類的樣本xi的第D個特征求和，再求平均值，即為第D個特征的質心。

Step4：若目標函數收斂，終止程序；否則轉到Step2。

Canopy的思想：在數據集中隨機點A，計算其余樣本與A的距離，根據距離的大小劃分類別。例如，小于T1的作為一類，[T1,T2]之間的為另一類。

采用Canopy算法優化K-means算法的過程如下。

(1) 原始數據存入數據集D中。

(2) 隨機確定中心點，放入canopy centerlist，將該數據從D里刪除。

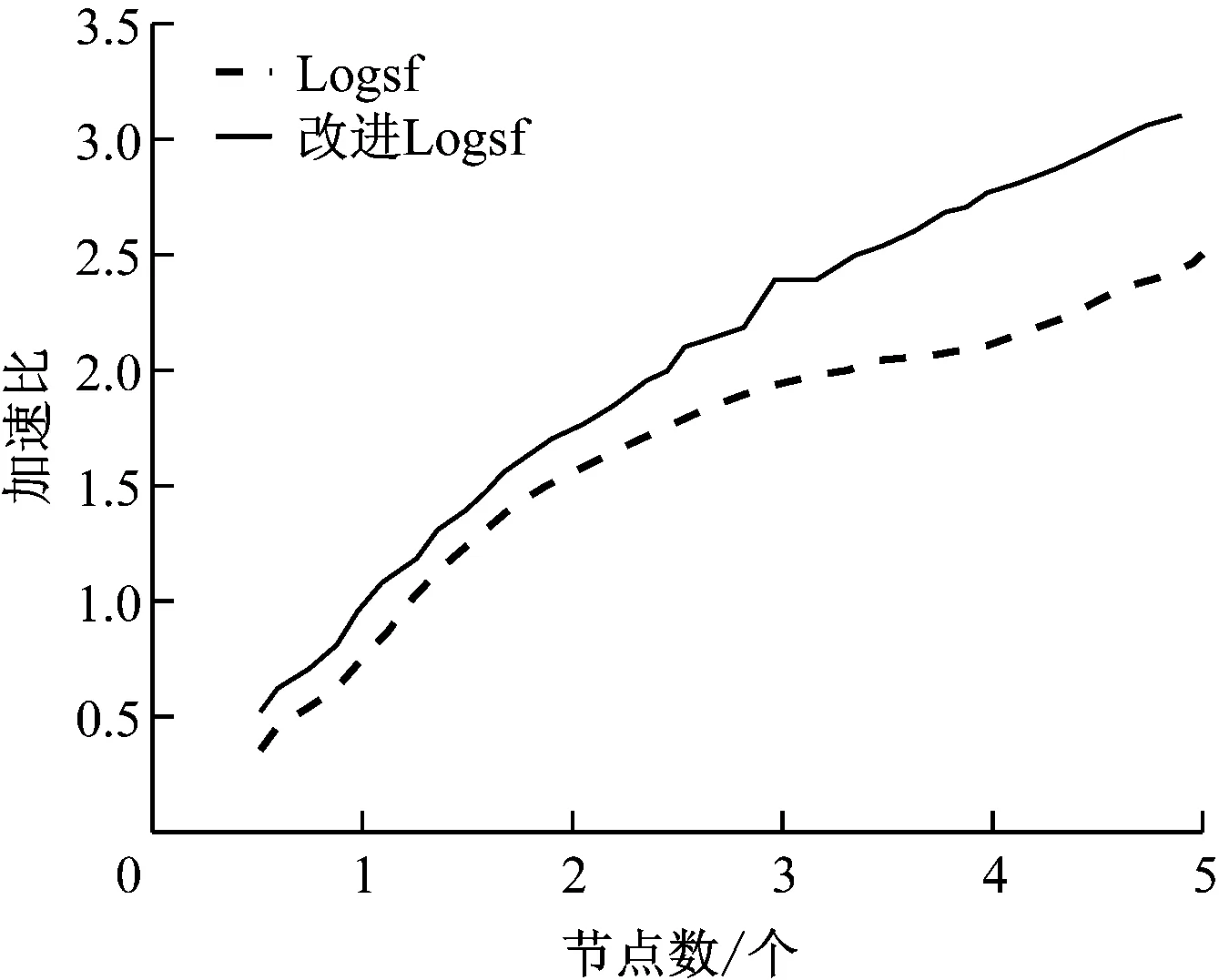
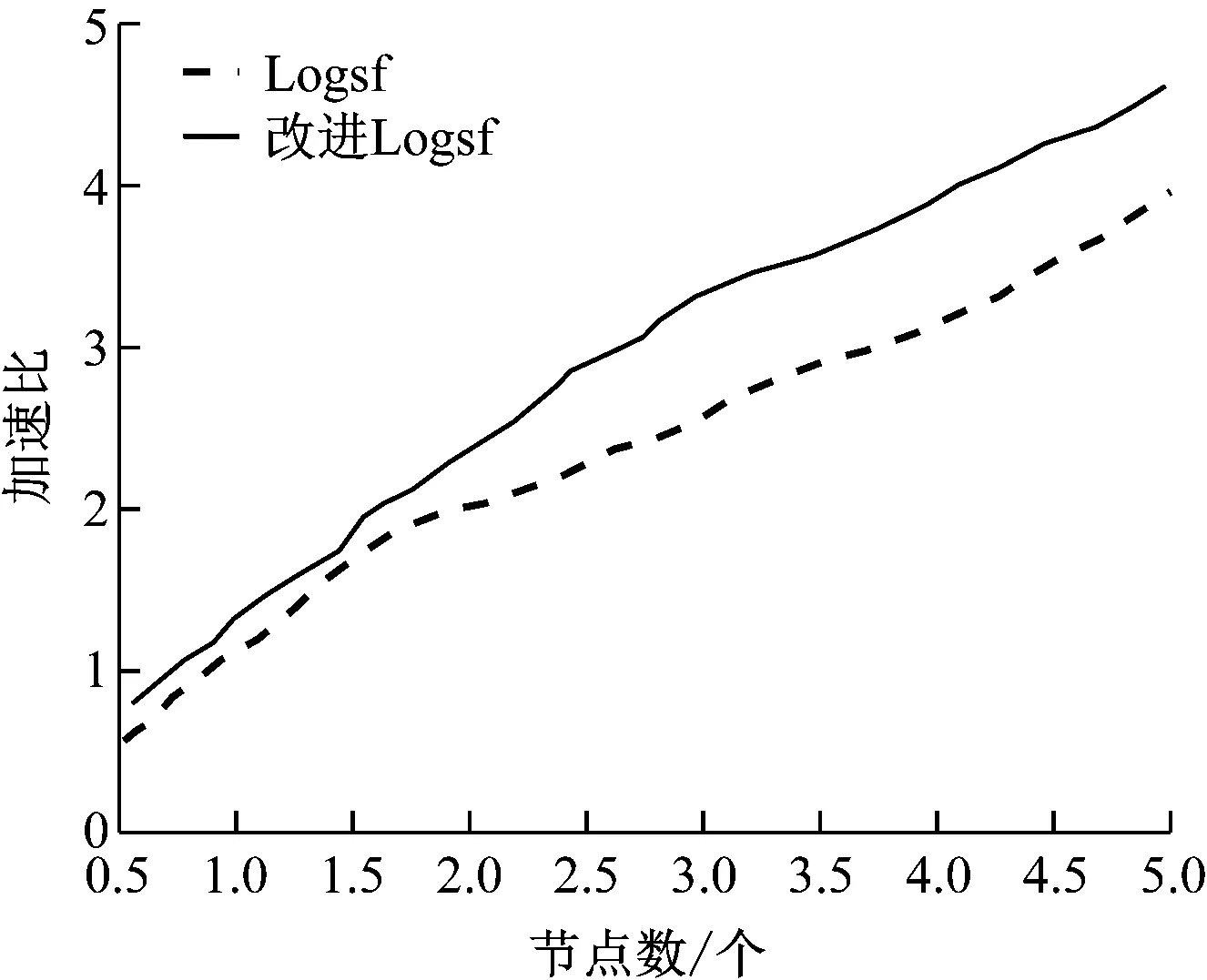
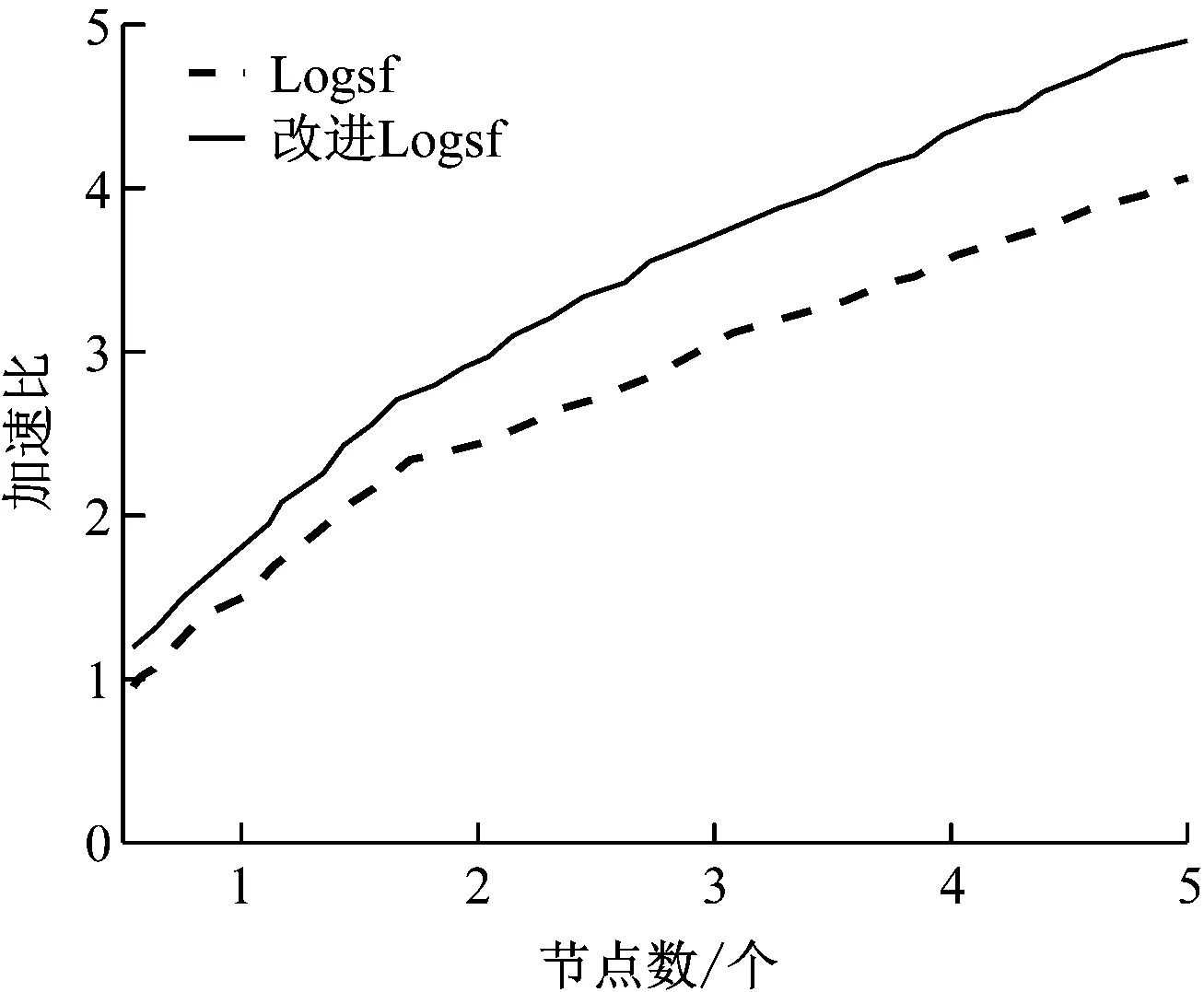
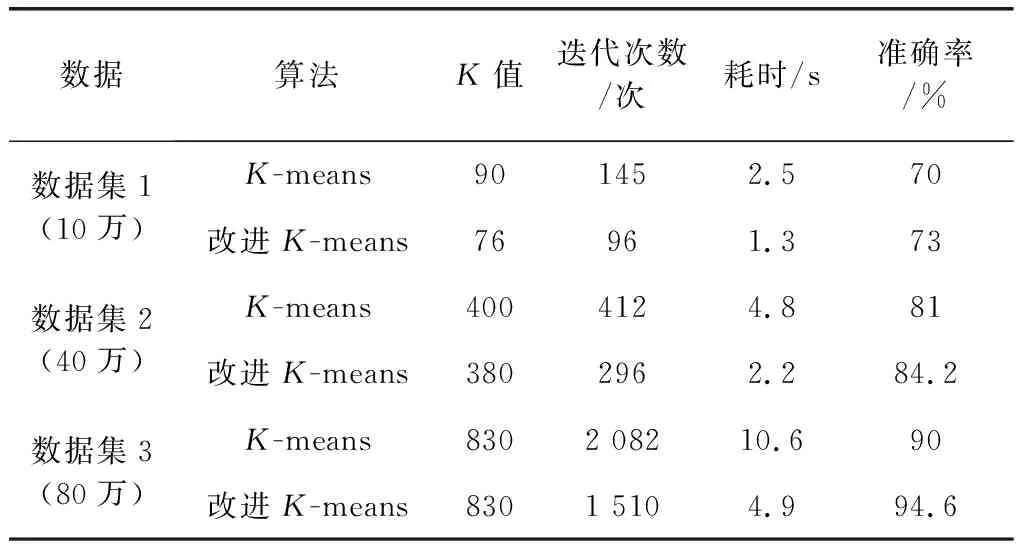
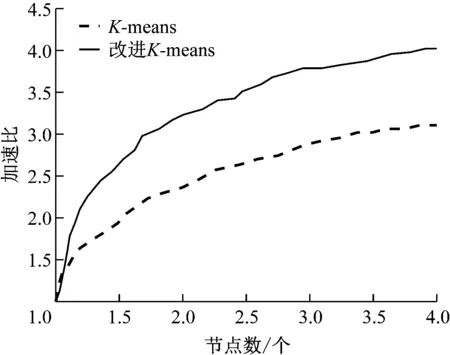
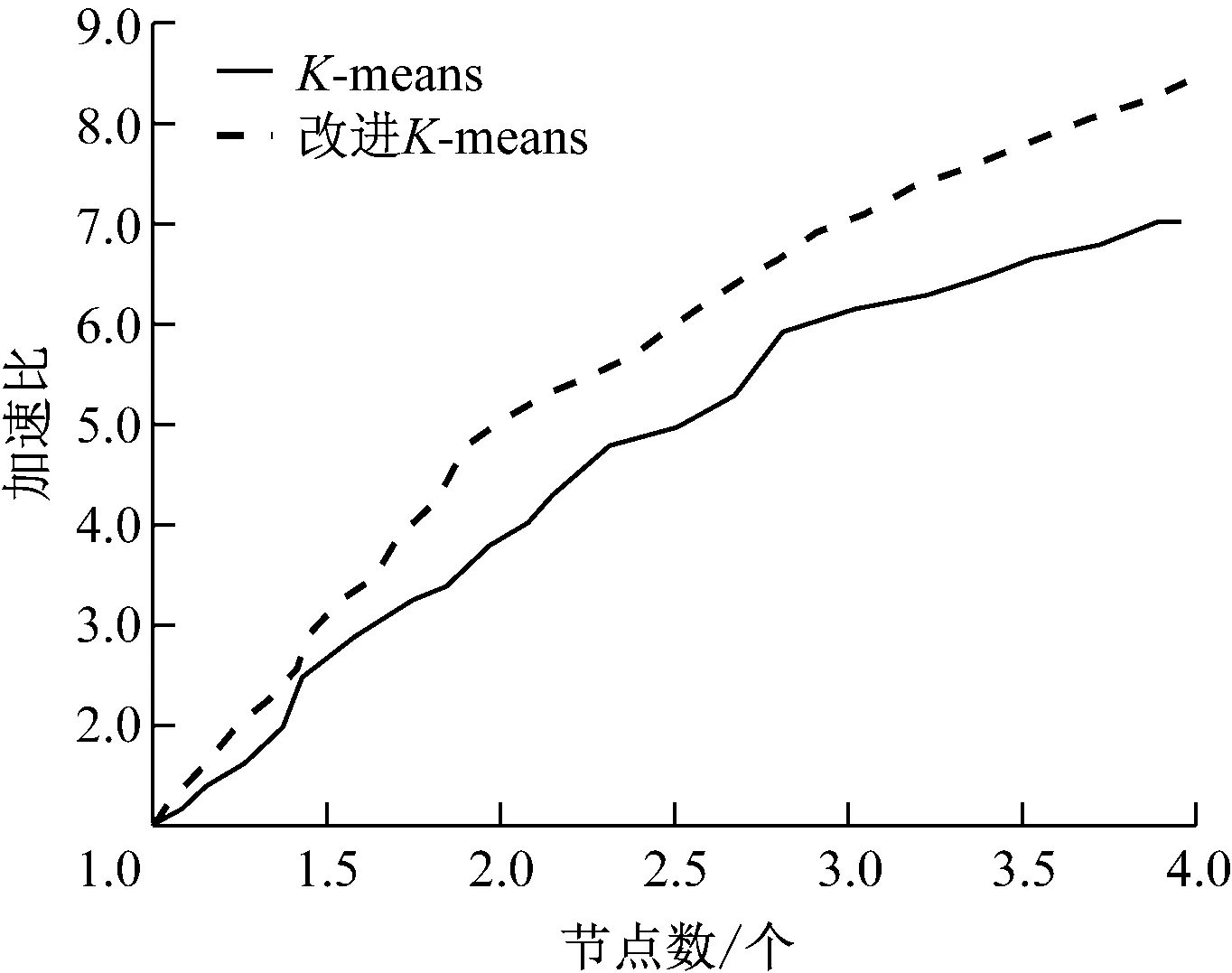
(3) 計算其他數據與canopy centerlist的距離。Dist[i]

(4) 通過歸類后得到了k個canopy。

(5) 計算k個聚類中心點。

(6) 計算每個數據與中心點的距離。將數據歸類為Dist[i]最小的類。

(7) 將各類的平均值作為新的中心點。

(8) 再計算新中心點與canopy中心點的距離，按照(3)分類。

(9) 若達到收斂條件，停止循環；否則繼續(6)—(8)。

具體流程圖如圖3所示。

圖3 Canopy-K-means算法流程圖

為了有效地對大數據進行降維和數據清洗，采用MapReduce方法，分別進行降維和數據清洗。在數據降維的時候，先采用梯度下降法求取最優權重值，采用Map函數根據權重大小將樣本按照〈key,value〉存儲。key為特征編號;value為數據編號。再采用Reduce函數將特征編號相同的樣本放在一起存儲到HDFS中。改進的K-means算法得到的異常數據，采用MapReduce方法處理也采用同樣的方法處理。

3 算例仿真

3.1 特征提取

為了驗證本文所提方法的有效性和可靠性，選取某企業的3種傳感器采集的信息進行仿真實驗。選擇其中10萬條數據(100MB)作為訓練集，另外分別選擇40萬條數據(200MB)和80萬條數據(800MB)作為測試集。采用改進的Logsf和Logsf方法進行實驗對比。各對比結果如圖4-圖7所示。

圖4 準確率對比曲線

圖5 訓練集的加速比曲線

圖6 測試集1的加速比曲線

圖7 測試集2加速比曲線

3.2 數據清洗

選取經過改進后的Logsf算法降維的數據，采用本文所提的改進K-means算法進行異常數據清洗。分別對其準確率、運行時間和加速比進行分析。準確率的對比結果如表1所示。

表1 兩種方法準確性對比

加速對比曲線如圖8-圖10所示。

圖8 10萬條數據加速比

圖9 40萬條數據加速比

圖10 80萬條數據加速比

3.3 結果分析

從圖4可以看出，隨著樣本數量的增加，改進的Logsf比傳統的Logsf方法準確性有了很大提升。雖然數據量較小的時候，改進的Logsf低于Logsf的準確性，但是本文處理的是大數據，所以圖4驗證了改進后的算法更適用于大數據的特征提取。從圖5-圖7的對比曲線可以看出改進的Logsf的加速明顯高于Logsf。以上實驗說明了改進后的Logsf算法的有效性。

從表1可以看出，在對異常數據進行清洗的時候，傳統的K-means算法準確率明顯低于改進的K-means算法，從圖8-圖10的加速對比曲線可以看出，在處理相同數量級的數據時，改進的K-means算法比K-means算法的加速比更快，驗證了本文所提方法的有效性。

4 總結

針對大數據中含有的異常數據清洗問題，本文提出了改進的Logsf方法，選擇特征，并進行數據降維處理，獲得約簡后的數據。采用Canopy方法對傳統的K-means算法進行改進。然后采用MapReduce方法實現算法并行化。實驗結果驗證了改進的Logsf方法比傳統的Logsf方法具有更高的特征提取準確度，改進的K-means算法比傳統的K-means算法清洗數據后，具有更高的準確度和更快的處理速度,驗證了本文所提方法的可靠性。