針對電費回收風險防控分析的用戶信用評分模型

田珂， 馬文棟， 王坤， 林偉， 李明亮

(1.國網河南省電力公司， 河南 鄭州 450000；2.國網河南省電力公司電力科學研究院 客戶服務中心， 河南 鄭州 450000；3.河南九域騰龍信息工程有限公司， 河南 鄭州 450000)

0 引言

收取電費是電力企業最重要的工作。按時計費不僅可以為稅收提供資金，以確保國家的財政收入，而且還可以為電力企業的可持續發展提供必要資金。隨著經濟社會的發展，供需形勢發生了很大變化，電費回收風險日益提高，如何評估該風險已經成為電力企業的重要問題。借鑒金融信貸機構的做法，對電力用戶進行信用評分，有助于電力企業識別高風險用戶群體，為降低電費回收風險提供數據支持。信用評分目標是區分優質用戶和不良用戶。為了提高電力用戶信用評分的效率，就需要電力企業利用大數據技術實施自動信用評分系統。

本研究的目的是描述使用人工神經網絡(ANN)模型和邏輯回歸(LR)模型作為預測電力用戶信用評分模型。已有研究比較了神經網絡對多元邏輯回歸的用戶信用預測能力。一些研究成果指出了監督學習的人工神經網絡相對于線性或邏輯回歸的優勢[1]。但是還沒有針對這2種方法的性能進行對比分析的研究。為此本研究介紹了神經網絡的概念性信息，并比較了神經網絡和邏輯回歸的性能，其中包括技術描述、參數變量選擇和模型評估。最后通過電力用戶信用評分試驗對比了2種方法在電力用戶信用數據分析方面的性能。

1 邏輯回歸模型

回歸模型通常用于研究多個自變量和因變量之間的關系，并確定與因變量相關的重要自變量。該模型還能夠描述自變量對因變量影響的大小和方向[2]。有兩種常見的回歸模型類別：線性回歸模型和邏輯回歸模型。選擇線性回歸還是邏輯回歸取決于因變量的度量范圍。如果因變量是二進制或二分類數據，則邏輯回歸可以提供更有意義的結果[3]。

與大多數其他預測建模方法一樣，邏輯回歸使用一組預測器特征來預測特定結果(目標)的可能性。 事件概率的對數變換的等式如式(1)。

Logit(pi)=β0+β1x1+β2x2+…+βkxk

(1)

其中,p為給定輸入的“事件”的后驗概率;x為輸入變量;β0為回歸線的截距;βk為系數。Logit變換是概率的對數，用于對后驗概率進行線性化并將模型中的估計概率結果限制在0到1之間。

1.1 變量選擇

通過變量選擇可以減少模型中獨立變量的數量，從而實現降低模型過度擬合的風險。通過檢查偽R平方和分類結果的準確性[4]來檢驗模型統計信息的擬合度。因此模型的評估指標需要滿足簡約的要求。簡約意味著如果將一些冗余變量排除在模型之外，現有的獨立變量將足以解釋結果變量。似然比卡方、Akaike信息準則(AIC)等擬合統計量都可用于變量選擇過程中模型擬合的測度[5]。

1.2 模型評估

如前所述，可以基于模型的統計數據和預測分類的準確性來評估順序邏輯模型的性能[6]。模型擬合統計量基于每次出現的預期和觀察頻率來測量模型擬合。另外，為了測量獨立變量和因變量之間的強度關聯，還可以使用取決于似然比的模型統計信息，例如偽R平方。在序數回歸模型中解釋偽R平方的方式與在線性回歸模型中解釋R平方的方式相似。偽R平方是模型在解釋數據變化或結果變量中自變量所占比例變化方面的性能指標。

2 人工神經網絡模型

神經網絡是適用于分析復雜的非線性關系的自適應模型。神經網絡由一組模擬神經元的處理單元(節點)組成。節點通過一組類似于突觸連接的權重互連到其他節點。這些連接允許信號并行和串行地通過網絡傳輸。突觸權重被解釋為跨節點的連接強度。節點是基于神經元模型的簡單計算元素，當達到一定的刺激水平時，神經元模型會產生動作電位。將到達節點的所有傳入信號的加權總和值與閾值進行比較。當超過閾值刺激時，節點將觸發；否則，節點保持為零。

通常神經網絡由三層組成：輸入層、輸出層和隱藏層，如圖1所示。

圖1的第一層加載了代表獨立(解釋性)變量的一個或多個神經元(節點)。而輸出層由一個或多個依存(結果)變量的神經元(節點)組成。輸出層表示模型的分類決策，其中每個決策類有一個節點。模型中的隱藏節點間接連接輸入層和輸出層。通常，一個或多個隱藏層位于輸入層和輸出層之間。

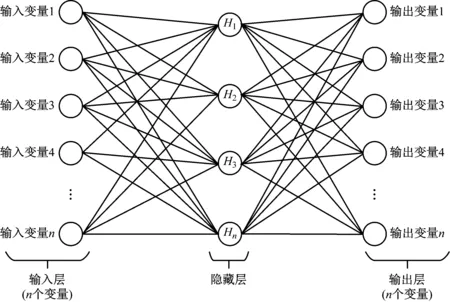
圖1 神經網絡結構

2.1 參數

人工神經網絡模型的核心元素是位于隱藏層中的神經元，在圖1中顯示為H1、H2、…、Hn。每個神經元通過網絡中設置的學習算法確定每個單獨輸入的最佳連接權重w=(w1、…、wn)。然后，神經元使用求和計算將來自每個輸入的加權值聚合為單個值。下一步是通過對總加權值應用激活函數來計算輸出[7]。在人工神經網絡模型中，特定的激活函數用于連接模型中的兩層。模型中使用的激活函數的類型取決于輸出層中的結果范圍。人工神經網絡模型中最常用的激活函數是S形激活函數，類似于Logistic回歸模型中使用的logit函數。S形激活函數如式(2)。

(2)

其中,η為閾值，x為加權值的總和。

分析神經網絡時要考慮的一個關鍵問題是過度訓練的可能性。過度訓練意味著網絡具有太多的迭代過程，可能會導致模型過度擬合。該模型產生的結果由于特定數據集中的數據存儲而無法推廣到整個用戶群體。本研究中防止模型過度擬合的一個方法是采用應用交叉驗證程序[8]。此過程將數據拆分為一定數量的子樣本。一些子樣本用作構建神經網絡模型的訓練數據集，而其他子樣本則用于驗證模型的性能。防止過度訓練中發揮重要作用的另一個因素是設置終止網絡訓練的條件。終止條件取決于為網絡選擇的體系結構和訓練算法。對于監督神經網絡模型，最廣泛的學習算法是反向傳播算法[9]。反向傳播算法中使用的參數包括動量、學習率和權重衰減系數[10]。

權重衰減系數用作權重降低因子以形成平滑的決策邊界，權重衰減通常在交叉驗證階段完成[11]。學習率決定了基于當前迭代的誤差在網絡中所占的百分比，而動量則決定了基于先前迭代的網絡中的誤差所占的百分比。動量、學習率和權重衰減系數較大幅度下降能夠加快網絡快速收斂，但是較大的下降幅度也會導致網絡無法收斂至全局最優[12]。

2.2 變量選擇

與其他統計模型構建過程一樣，人工神經網絡模型的性能可能會受到輸入層中使用的變量數量的影響。另外，可以將人工神經網絡模型與其他統計模型(例如回歸模型)結合使用，以減少輸入變量的數量。 減少輸入變量數量的另一種可能性是通過檢查由人工神經網絡模型得出的連接權重[13]。具有低連接權重的變量應該被去除。然后，人工神經網絡模型需要在迭代過程中逐步完成去除低權重變量和評估模型性能的計算操作。

2.3 模型評估

評估人工神經網絡模型質量的潛在標準之一是識別性能，這是衡量數據集中兩個類別的分離程度的一種度量。評估人工神經網絡模型中的識別性能的方法是敏感性、特異性、準確性和ROC曲線。模型的靈敏度指出預測模型的真實陽性，而1-特異性表示假陽性率。通過針對各種閾值概率繪制針對1-特異性的靈敏度，可以得出ROC來評估人工神經網絡模型的性能。

3 模型對比

盡管人工神經網絡模型和邏輯回歸模型的結構和表達方式迥異，但是這兩個模型背后的思想基本相同。例如人工神經網絡模型的“連接權重”和邏輯回歸模型“系數”的作用類似。此外，人工神經網絡模型根據嵌入到網絡中的激活函數來調整連接權重，而邏輯回歸模型則使用其鏈接函數來估計其系數。人工神經網絡模型中應用的學習和訓練過程類似于邏輯回歸模型中的參數估計過程。另一個相似之處與模型中使用的變量數量有關。邏輯回歸和人工神經網絡模型構造遵從簡約原則，即只要模型能夠充分說明自變量對結果變量的影響，則在模型中使用較少的自變量并排除不必要的變量[14]。

相對于邏輯回歸模型，人工神經網絡模型的不同之處在于可以在輸入變量之間存在復雜非線性關系的前提下表現出強大的學習能力。雖然邏輯回歸模型在函數中包含了指數項的前提下也具有類似的處理自變量和因變量之間的非線性關系的能力，但是該模型需要先驗已知的非線性關系形式。人工神經網絡模型不需要先驗模型規范，因為網絡具有基于數據模式學習層之間關系的能力。因此，人工神經網絡模型能夠提供更多的靈活性和更高的魯棒性。

相對于人工神經網絡模型，邏輯回歸模型具有更好地解釋輸出變量和輸入變量之間關系的性能。而人工神經網絡模型無法揭示輸出變量與輸入變量之間的變化關系。因此，邏輯回歸模型能夠更好支持對輸入變量的敏感性分析，能夠更直觀地確定模型中每個輸入變量對輸出變量的影響程度。

人工神經網絡模型是基于迭代過程構建的，因此該模型能夠學習輸入變量和輸出變量之間復雜的非線性關系。人工神經網絡模型中的連接權重比邏輯回歸模型中的系數更加抽象、更難解釋。人工神經網絡模型中隱藏層的數量越多，則神經節點之間連接權重和相互依賴性的關系越復雜。由此可見，人工神經網絡模型更適合作為預測分類的統計性模型，而不是解釋性的模型。而邏輯回歸模型中的模型參數可以較容易地對應某個預測變量的權重，從而可以對該參數進行統計測試以檢查每個參數對模型的重要性。因此邏輯回歸模型的優點在于模型參數的可解釋性和易用性，而人工神經網絡的優點在于強大的變量之間非線性關系的處理能力。

人工神經網絡還存在一個問題是設計和優化網絡拓撲需要一個非常復雜的實驗過程。這是因為隱藏層中層數和神經元數量、不同的激活函數和初始權重值可能會影響最終分類結果。此外，人工神經網絡還需要大量的訓練樣本和較長的學習時間。

4 實驗驗證

本研究使用了2017年1月至2018年12月來自鄭州電力公司的697個低壓電力用戶群體的真實數據。實驗數據集包含客戶信息，例如個人特征、可支配收入、職業、就業時間、房屋所有權、與宏觀經濟背景有關的變量以及是否存在以往延遲繳納電費行為。實驗的目的是預測3個月內遲交電費的可能性。

邏輯回歸模型和人工神經網絡模型用于分析數據。兩種模型都使用SAS Enterprise Miner 6.2進行了分析。實驗將數據分為訓練數據集(60%)和驗證數據集(40%)。本實驗使用錯誤分類率來衡量所構建的兩個模型的性能。錯誤分類率是所有類別的總錯誤分類與特定分類問題中樣本總數的比率。較低的誤分類率表示較好的分類性能。SAS Enterprise Miner 6.2中構建的模型流程如圖2所示。

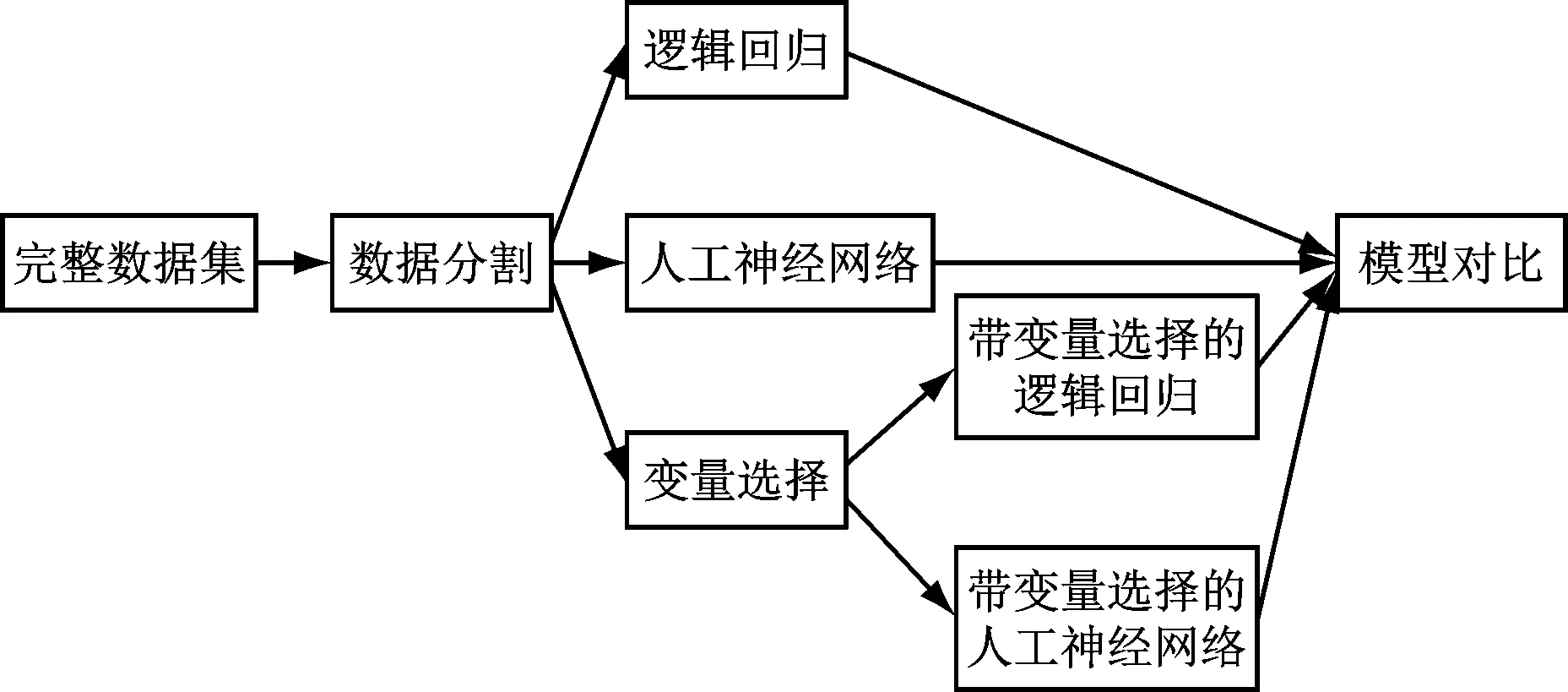
圖2 模型流程

使用logit函數構建邏輯回歸模型，并使用逐步聚合方法構建2個邏輯回歸模型。一個模型前面有變量選擇以減少模型中輸入變量的數量，而另一個模型則沒有。本實驗應用了基于R平方準則的變量選擇。將要包含在模型中的輸入變量的最小R平方設置為0.15。根據變量選擇結果，14個項目中只有9個被用作模型中的輸入變量。

本實驗建立的人工神經網絡模型將多層感知器體系結構與一個隱藏層和反向傳播學習算法結合使用。權重衰減系數設定為0.01，學習速度和動量設定為0.1和0.01。建立了兩個神經網絡模型。一種是變量選擇，另一種則不是。變量選擇也基于R平方準則。每種模型的誤分類率如表1所示。

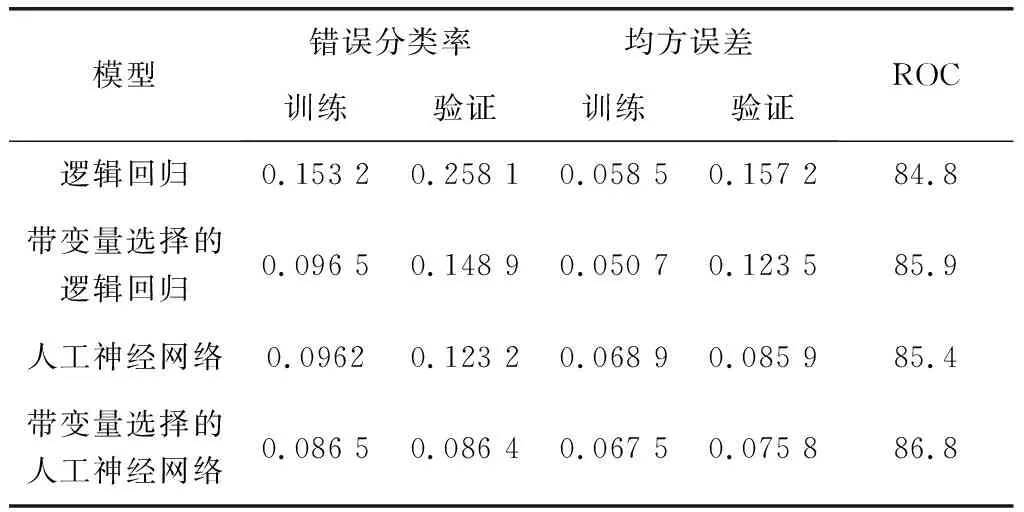
表1 每個模型的分類錯誤率

表1中顯示的結果表明，有和沒有變量選擇的2種人工神經網絡模型都比驗證數據集中的邏輯回歸模型具有更低的誤分類率。另一方面，在訓練數據集中，這2種邏輯回歸模型的誤分類率均低于人工神經網絡模型。此外，表1還顯示了人工神經網絡模型的ROC指數較高。一個好的模型是具有相對穩定的錯誤分類率(較高的錯誤分類率會導致更多訓練和驗證的迭代次數)以及較高的ROC指數的模型。因此，在評價指標下，人工神經網絡模型是一個更好的模型。結果還表明變量選擇降低了錯誤分類率，邏輯模型的降低率比人工神經網絡模型中的降低率更高。具有變量選擇的邏輯回歸模型的輸出和具有變量選擇的人工神經網絡模型所產生的前4個輸入變量的權重,如表2、表3所示。

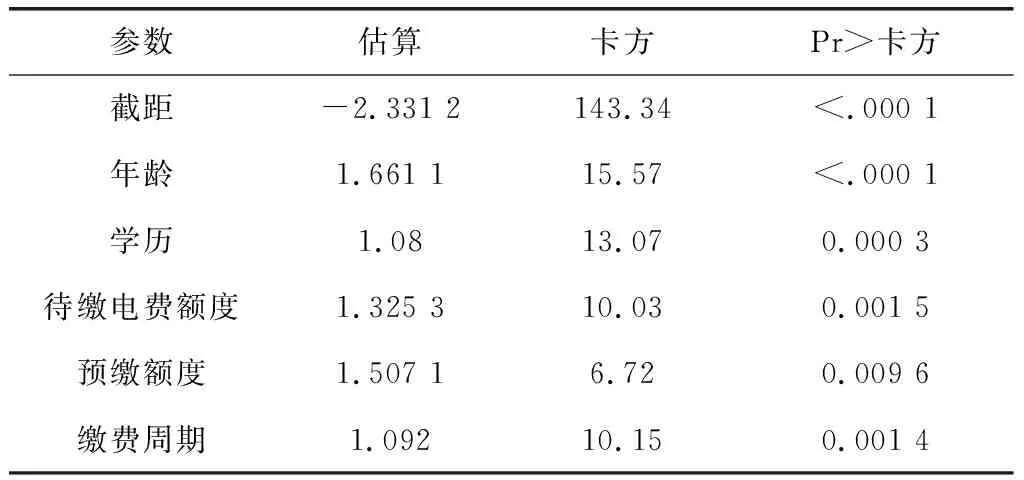
表2 邏輯回歸模型的權重估計

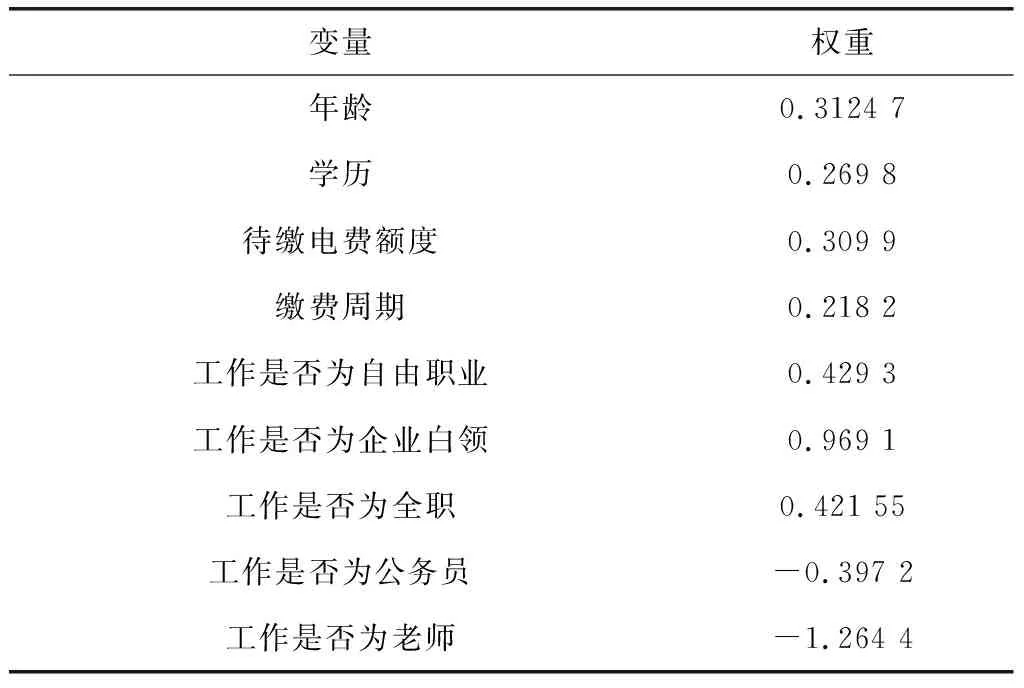
表3 人工神經網絡模型的權重估計

表2和表3指出邏輯回歸和人工神經網絡模型之間沒有主要差異。根據這2種模型，年齡是預測違約概率最重要的變量。邏輯回歸模型的下一個重要變量是學歷，而人工神經網絡模型的第二重要的變量是待繳電費金額。

人工神經網絡、具有變量選擇的人工神經網絡和邏輯回歸的ROC曲線的比較如圖3所示。

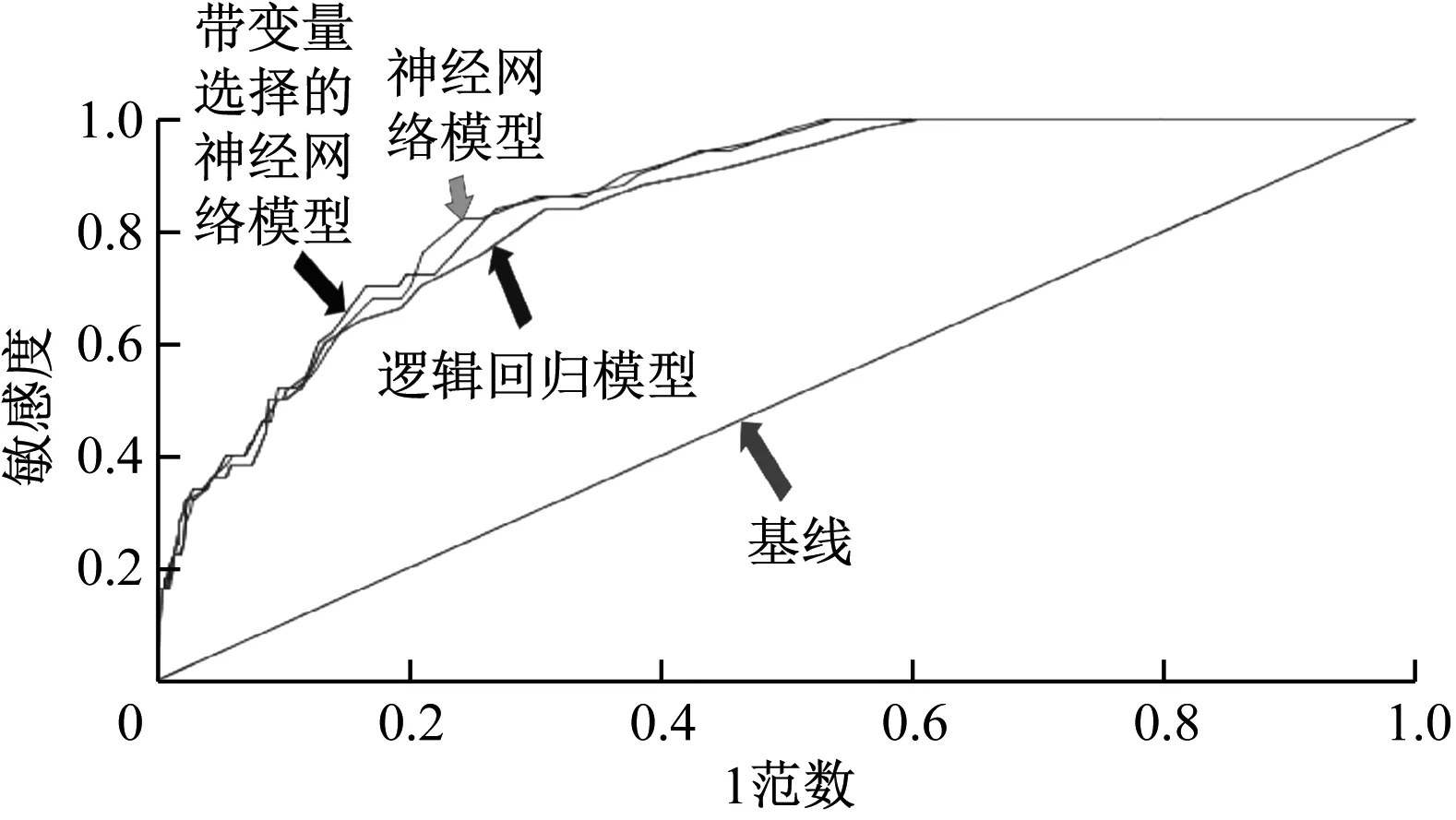
圖3 ROC曲線

通過查看ROC曲線，無法準確預測哪個模型是好的，因為三條ROC曲線下的面積都只有微小的變化。由表1可知，具有變量選擇的人工神經網絡具有較高的ROC指數。因此，通過使用誤分類率和ROC評價指標，可以確定具有變量選擇的人工神經網絡模型是更好的選擇。

5 總結

在本研究所述的研究工作中對邏輯回歸和人工神經網絡(ANN)在電力用戶信用評分預測中的應用進行了闡述，概述了這2種模型的共同原理及其區別，展示了邏輯回歸和ANN模型的構建方法以及構建過程中應考慮的細節以及如何對其進行評估。

本研究表明，神經網絡模型或邏輯回歸模型的構建，沒有特定的參數和規則可以遵循，并且每個模型都有其優點和缺點，因此在使用這2種模型對電力用戶信用進行評估時需要反復實驗以確定模型的變量和參數，以取得靈活性和過度擬合之間的平衡。