一種提高舵機系統動態特性的插值方法

張少應, 陳明哲

(1. 西安航空學院計算機學院， 陜西 西安 710077； 2. 西安電子工程研究所， 陜西 西安 710100)

0 引言

在對舵機系統施加正弦激勵信號，進行頻率特性測試過程中，舵機指令的密度往往對測試結果起到了至關重要的作用。指令越密集，舵機位置反饋測試曲線越平滑，跟隨指令的實時性越好。反之，指令越稀疏，低頻時舵機系統的相位延遲越大，高頻時舵機位置反饋測試曲線的失真度越高。

為了適應不同密度的舵機指令，保持舵機系統頻率特性測試數據的一致性，可以利用插值的方法對指令進行插值計算[1]。插值法種類較多，包括拉格朗日多項式插值、分段線性插值及三次樣條插值[2]。在實際應用中，往往要綜合考慮插值的精度、效率、運算量等因素來選擇合適的插值方法。

本文采用拉格朗日(Lagrange)外插法估算舵機的位置指令，替代接收到的位置指令，通過增加指令點數，注入更加平滑的位置參考輸入，從而改善系統的動態響應性能[3]。

1 插值原理

根據給定的函數表構造一個既能反映函數f(x)的特性，又便于計算的簡單函數p(x)來近似f(x)，并使得p(xi)=f(xi)，(i= 0,1,2,…,n)，這就是插值法[4]。

Lagrange插值是n次多項式插值方法，可以給出一個恰好穿過二維平面上若干個已知點的多項式函數。

對某個多項式函數，已知有給定的n+1個取值點為式(1)。

(x0,y0), (x1,y1),…, (xi,yi),…,(xn,yn)

(1)

其中，xi對應著自變量的位置，而yi對應著函數在這個位置的取值。

假設任意兩個不同的xi都互不相同，那么應用Lagrange插值公式所得到的Lagrange插值多項式為式(2)。

(2)

其中，每個li(x)(i=0,1,2,…,n)為Lagrange基本多項式(或稱插值基函數)，其表達式為式(3)。

(3)

1.1 線性插值

當n=1時，Lagrange多項式插值為線性插值，表示為式(4)。

L1(x)=y0l0(x)+y1l1(x)

(4)

用通過兩點(x0,y0)、(x1,y1)的直線y=L1(x)來近似代替曲線y=f(x)，其中插值基函數為式(5)、式(6)。

(5)

(6)

1.2 拋物線插值

當n=2時，Lagrange項式插值為拋物線插值，表示為式(7)。

L2(x)=y0l0(x)+y1l1(x)+y2l2(x)

(7)

用通過三點(x0,y0)、(x1,y1)、(x2,y2)的拋物線y=L2(x)來近似代替曲線y=f(x)，其中插值基函數為式(8)—式(10)。

(8)

(9)

(10)

1.3 外推算法

插值包括內插(Interpolate)和外推(Extrapolate)兩種算法。內插算法：通過已知點的數據推求同一曲線上未知點數據。外推算法：通過已知曲線上的數據，推求曲線之外區域的數據[5]。Lagrange插值公式內插算法和外推算法都適用。

頻率特性測試時，舵機系統指令的幅度為1°的離散正弦指令，即式(11)。

y=f(t)=1°sin(ωt)

(11)

其中，ω為角頻率，單位rad/s；指令間隔時間ΔT為5 ms。為提高指令密度，在每2個5 ms指令之間插入4個指令，將指令間隔時間ΔT縮小到1 ms。

為提高舵機指令的實時性，可采用外推算法對指令進行預測，預測算法可以有效減小延遲影響[6]。根據已知的前幾個時刻的指令及當前時刻的指令，分別用線性外推法和拋物線外推法來預測下一個5 ms內的正弦指令變化趨勢。

1.4 外推公式推導

(1) 線性外推

線性外推法是最簡單的預測法，根據已知兩點確定的直線來推斷事物未來的變化。設(x0,y0)、(x1,y1)分別為-5 ms、0 ms時刻的指令坐標，根據式(5)、式(6)計算直線的插值基函數，為式(12)、式(13)。

(12)

(13)

根據式(4)得線性外推的指令計算式為式(14)。

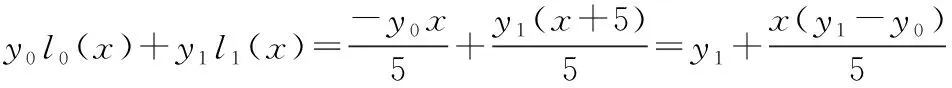
(14)

(2) 拋物線外推

拋物線外推法根據已知3點確定的拋物線來推斷事物未來的變化。設(x0,y0)、(x1,y1)、(x2,y2)分別為-10 ms、-5 ms、0 ms時刻的指令坐標，根據式(8)—式(10)計算拋物線的插值基函數，為式(15)—式(17)。

(15)

(16)

(17)

根據式(7)得拋物線外推的指令計算式為式(18)。

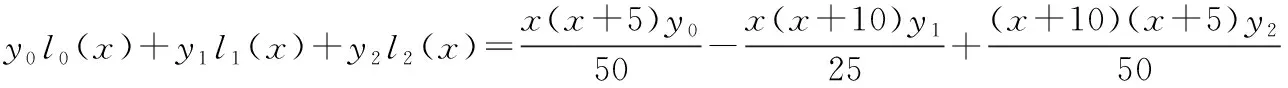
(18)

在式(14)、式(18)中，x為時間變量，單位ms，取值為0，1，2，3，4。

1.5 外推算法實現

軟件中設置1 ms中斷定時器，用于插值計算。實現方法如下。

(1) 當接收到新的舵機位置指令時，將插值計數值清零，即x=0；并將當前的新指令(0m時刻)作為掃頻指令；同時進行指令迭代，更新并保存最近2次(線性外推法)或3次(拋物線外推法)的指令；

(2) 當定時器中斷發生時，插值計數值x加1，即當x等于1，2，3或4時，根據式(14)或式(18)計算插值后的指令，并將該指令作為本次的掃頻指令；

(3) 當插值計數值x等于5時，將計數值x清零，即x=0；

(4) 重復前面的步驟1—3，可實現指令插值。

2 仿真驗證

在MATLAB/Simulink下，編寫用戶自定義的線性外推和拋物線外推函數，對5 ms正弦掃頻指令進行1 ms插值。1°，3 Hz離散正弦指令的插值仿真圖如圖1所示。1°，10 Hz離散正弦指令的插值仿真圖如圖2所示。

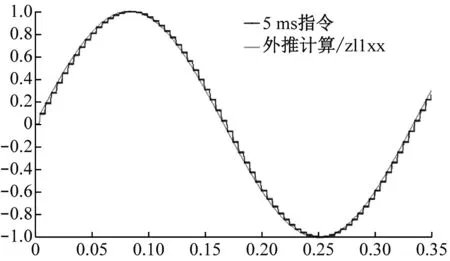
(a) 3 Hz線性插值

從圖1、圖2中可以看出，指令經過插值曲線更加平滑；指令插值后正弦曲線的相位整體前移；指令頻率較低(3 Hz)時，線性插值和拋物線插值效果一致，當指令頻率較高(10 Hz)時，拋物線插值的效果明顯優于線性插值，因此高頻時優選拋物線插值。

在Simulink下，保持某舵機系統所有控制參數不變的條件下，將拋物線插值后的指令作為正弦激勵信號，對舵機系統的頻率特性進行仿真。1°，3 Hz正弦指令插值前后舵機系統的動態響應情況，如圖3所示。

從圖3中可以看出，指令插值后，舵反饋信號跟隨指令信號的實時性更好；當指令過零點時，舵反饋信號過零點的時間在插值前是0.352 s，而在插值后是0.344 s，滯后時間減小了8 ms。

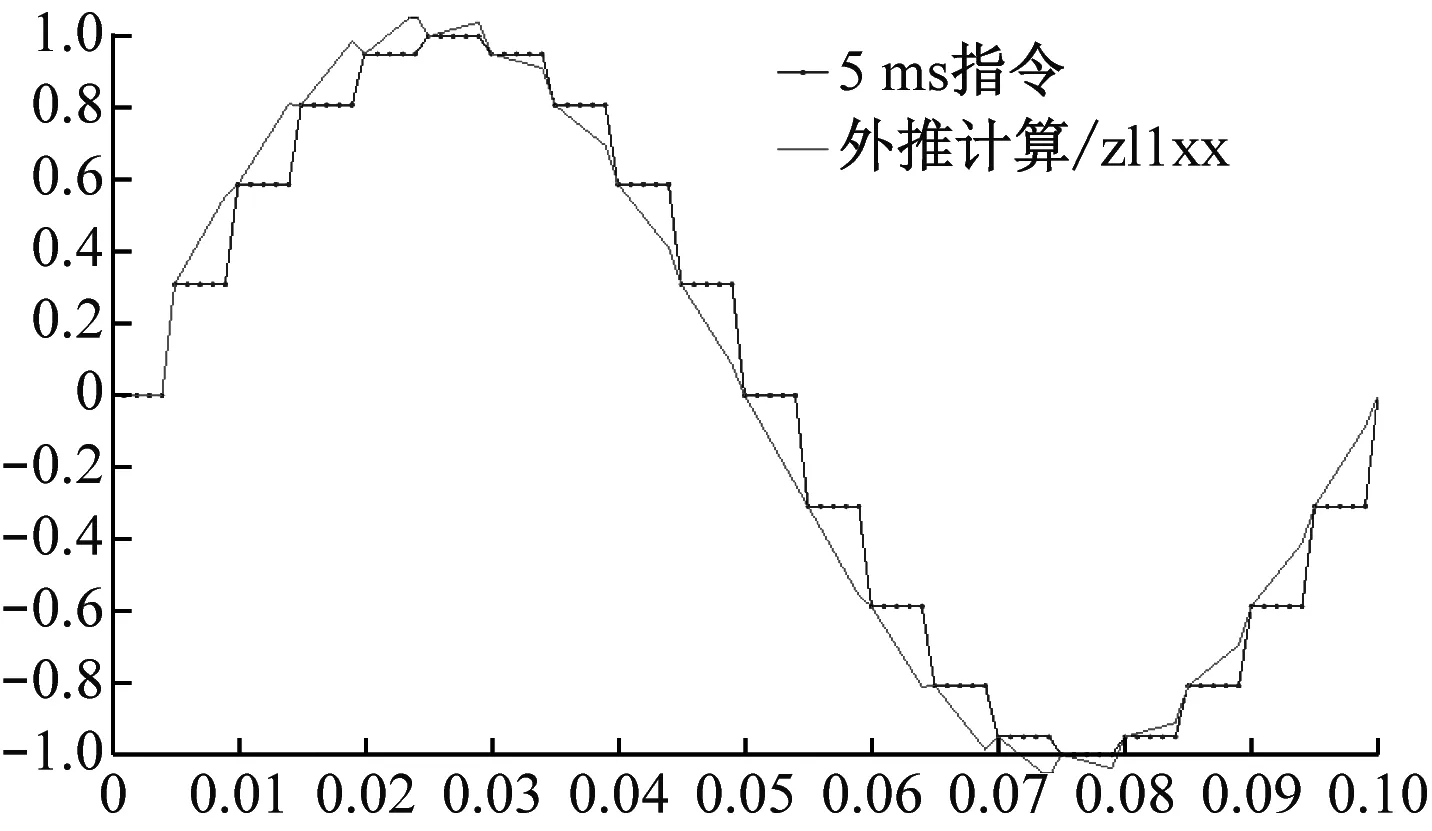
(a) 10 Hz線性插值

(a) 插值前頻率特性

3 測試驗證

針對某舵機系統頻率特性測試時，低頻相位超差問題，在不改變系統物理特性的條件下，僅更改了控制軟件，對5 ms測試指令采取了1 ms拋物線插值處理。經測試，舵機系統相位延遲明顯改善，測試結果如表1所示。

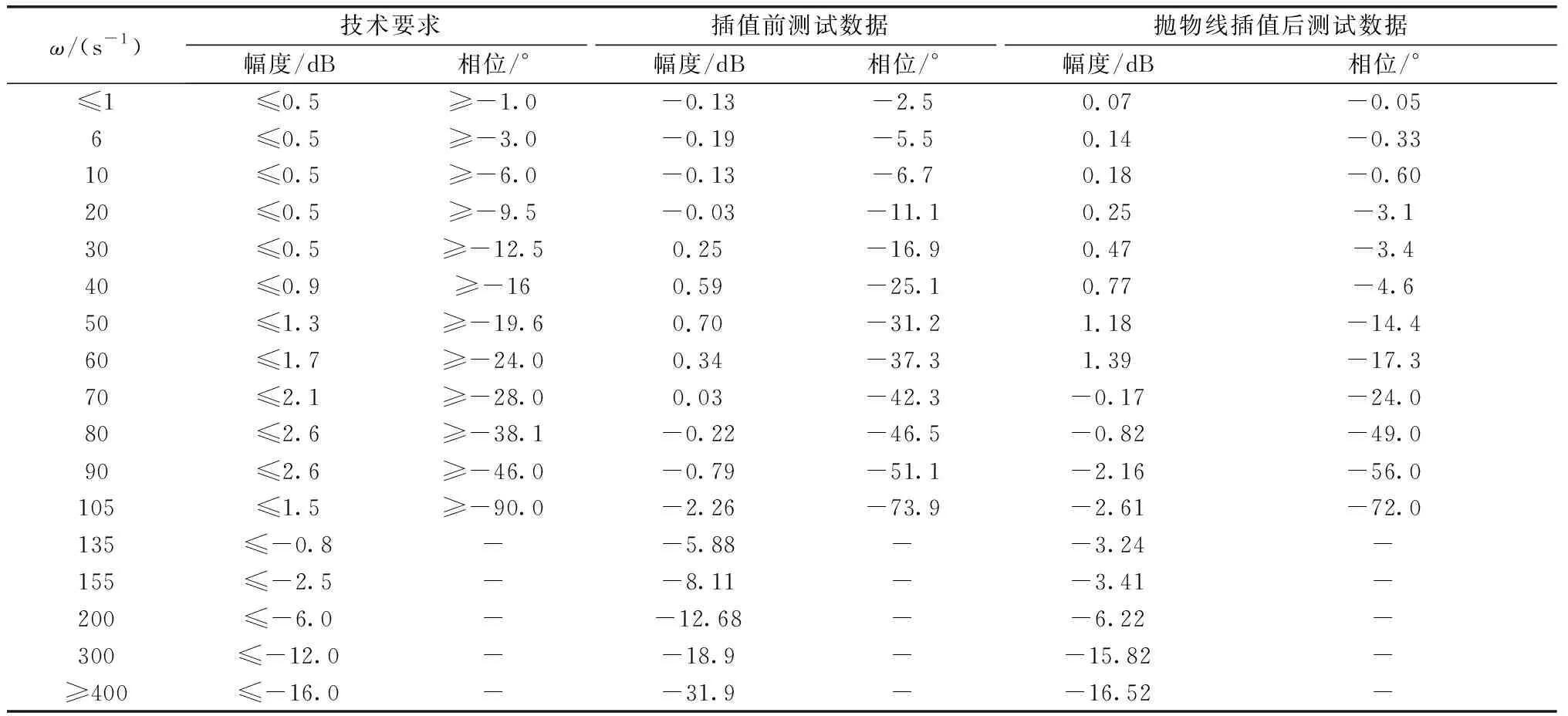
表1 頻率特性測試比對表

控制軟件增加插值后，對軟件進行回歸測試，分別施加正弦、方波及三角波指令對舵機系統的功能及性能進行測試。測試發現：當正弦指令的頻率大于10 Hz時，指令插值對系統相移指標沒有影響。因此，增加了指令插值的限定條件，僅當指令變化不大于0.3°時進行插值，這樣有效降低了高頻正弦指令在波峰和波谷處的失真度。

4 總結

對舵機系統位置指令進行外推插值細分，獲得在時間上更加密集的指令數據，是減小舵機系統低頻相位延遲行之有效的方法。它不需要更改舵機系統的硬件，只需對軟件進行局部更改，就能顯著提高系統的頻率特性。該方法具有計算簡單、易于工程實現的特點，既可以有效消除系統的延遲，又不會因為算法本身的復雜性而產生新的系統延時。