借助思維可視導引 優化高三復習效果*

陸 麗

(江蘇省太倉高級中學 215411)

數學是理性的，而學生的數學思維是隱性的、不可視的.因此，教師要在充分了解學生的思維情況的基礎上組織教學.思維可視導引教學，就是以圖示或圖示組合的方式，將抽象的數學研究對象變得可視，讓學生在基本活動經驗聚集的過程中打開思維的大門，讓內隱的數學思維展露出來.它有利于教師有效引導，可促進課堂教學的高效開展，實現數學知識、方法、思想的主動建構，優化學生的思維品質.它不僅是一種教學策略與方法，更是一種教學思想與觀念.本文以高三微專題復習課“與三角函數有關的導數問題”為例說明如何借助思維可視導引，優化高三復習的效果.

1 導圖探路，明晰思維方向

在高三教學中，教師要認真研讀課標，研究高考評價體系，使學生深刻領悟“為什么學”(高考要求)、精準聚焦“學什么”(要解決的問題)、具體實現“怎么學”(需要經歷怎樣的歷程，如何達到).如果能將教學目標、教學重點及難點有效融入到思維導圖中，借助思維導圖讓學生明晰思維方向，這將大大促進學生提升學習意識和思維能力.

教學片段1呈現表1，指出與三角函數有關的導數綜合問題是近幾年高考命題的一個重要方向.觀察這些考題，從函數解析式的形式看，它們是三角函數與多項式函數、分式函數、指數函數與對數函數疊加的復雜函數；從研究問題的類型看，它們涉及到考查函數的單調性、最值、極值、零點及不等式恒成立等問題，其本質就是研究這些復雜函數的性質.最終教師給出思維導圖(圖1)，指出本節課的教學目標：如何研究這些與三角函數有關的復雜函數的性質，有哪些方法.

表1

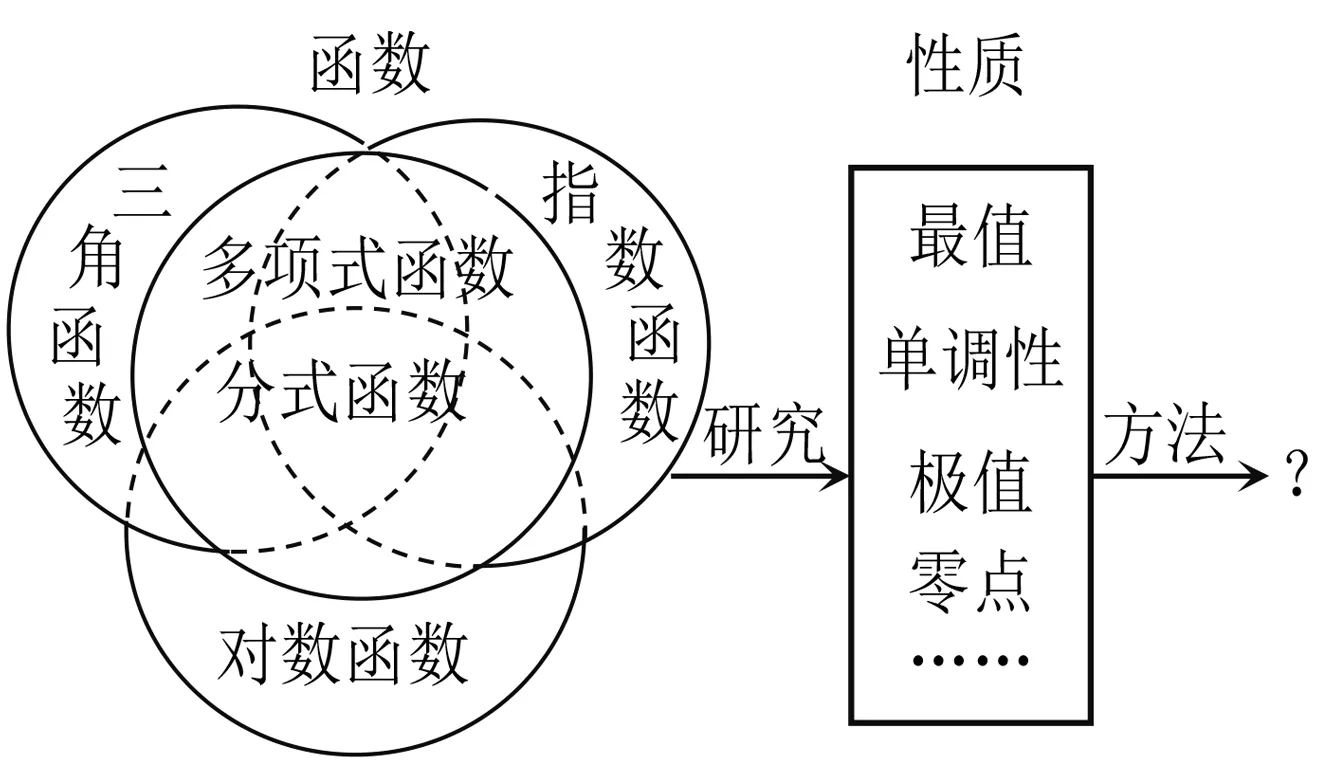
圖1

本片段看似簡單，實則起到了對本節課核心問題的定位作用，能激發學生應用所學知識、方法解決相關問題.同時，借助思維導圖，讓課堂目標清晰可視，為學生提供了可視化的思維路徑，便于學生有序開展研究.

2 探究留痕，呈現思維軌跡

課堂上學生的參與不僅是行為上的參與，更是思維上的參與.教師要嘗試通過各種方式激活學生的思維，培養學生的思維品質.在高三教學中，數學思維伴隨數學解題探究的全過程，這些內容如果僅憑有限的記憶是不夠的，更需要我們將題目的條件、目標、解題思路、各解題方法的適用條件及可能遇到的困難，甚至一些轉瞬即逝的想法清晰地記錄下來，留下思維軌跡，便于學生認識數學知識的本質，更能認識數學方法之間的關聯，從而優化解題策略.

教學片段2教師給出以下四個熱身練習題：

1．(2018全國卷I理第16題)已知函數f(x)=2sinx+sin 2x，則f(x)的最小值是．

2．函數f(x)=x2-4xsinx-4cosx在 (-π,π)上的零點個數是( ).

A.1 B.2 C.3 D.4

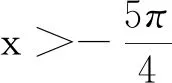
3．若關于x的不等式ex+cosx≥a+2在 [0,+∞)上恒成立，則實數a的最大值是( ).

A.0 B.1 C.2 D.3

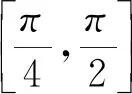
在高三復習中，很多學生喜歡總結出一定的解題模式，然后機械地套用固定模式解題，這樣學生的思維容易固化，形成一定的思維定勢，不利于發展創新思維．很多學生在遇到與三角函數有關的導數問題時，都不假思索地進行求導研究，一次求導不行，再二次求導，甚至三次求導．針對這樣的固化思維，教師設計了熱身練習1和2，旨在讓學生能夠借助函數式的特征分析，如函數的性質(奇偶性、周期性)簡化研究對象，從而將整體問題轉化為局部問題，再借助導數工具研究局部問題．

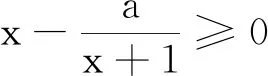
在每個熱身練習探究的過程中，教師及時將問題、思路、方法、技巧等一點點地記錄下來，思維的路徑抽絲剝繭般地在圖示上一步步呈現出來，形成了下面的思維軌跡圖，這就使學生學習有跡可循，使其中蘊含的數學規律自然地“浮出水面”，形成方法體系．

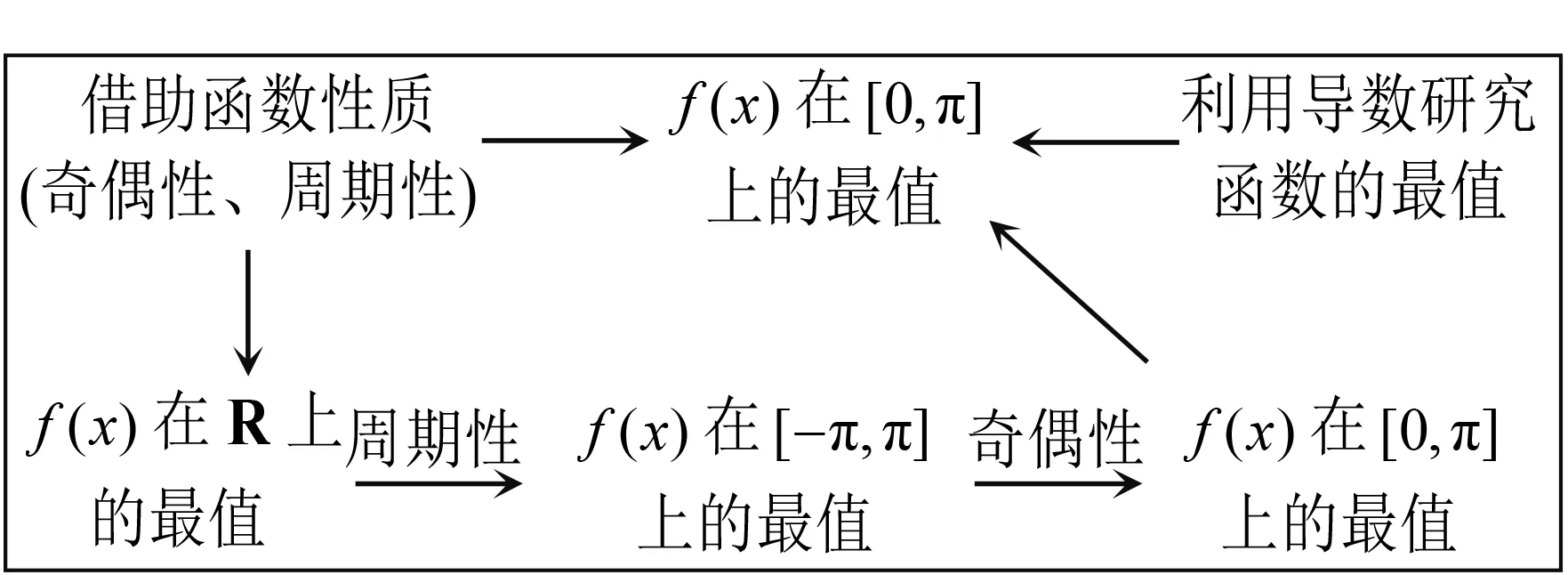
圖2 熱身練習1思維軌跡

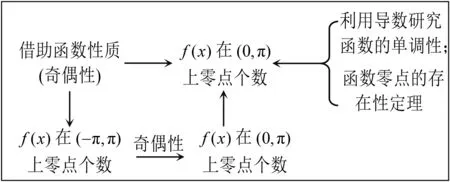
圖3 熱身練習2思維軌跡

圖4 熱身練習3思維軌跡

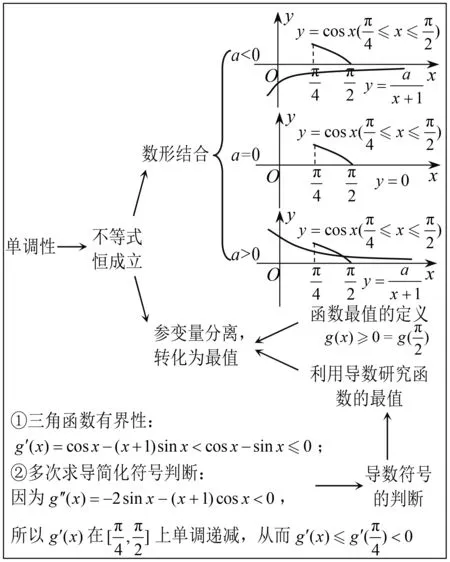
圖5 熱身練習4思維軌跡

3 多維表達，物化思維成果

讓思維可視，需要調動學生的多種器官參與課堂活動，將課堂中的探究發現運用數、形、結構等多種數學表征方式表達出來，物化思維成果．

教學片段3教師給出以下例題：

方法1：從數的角度表征

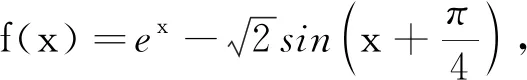
方法2：從形的角度表征

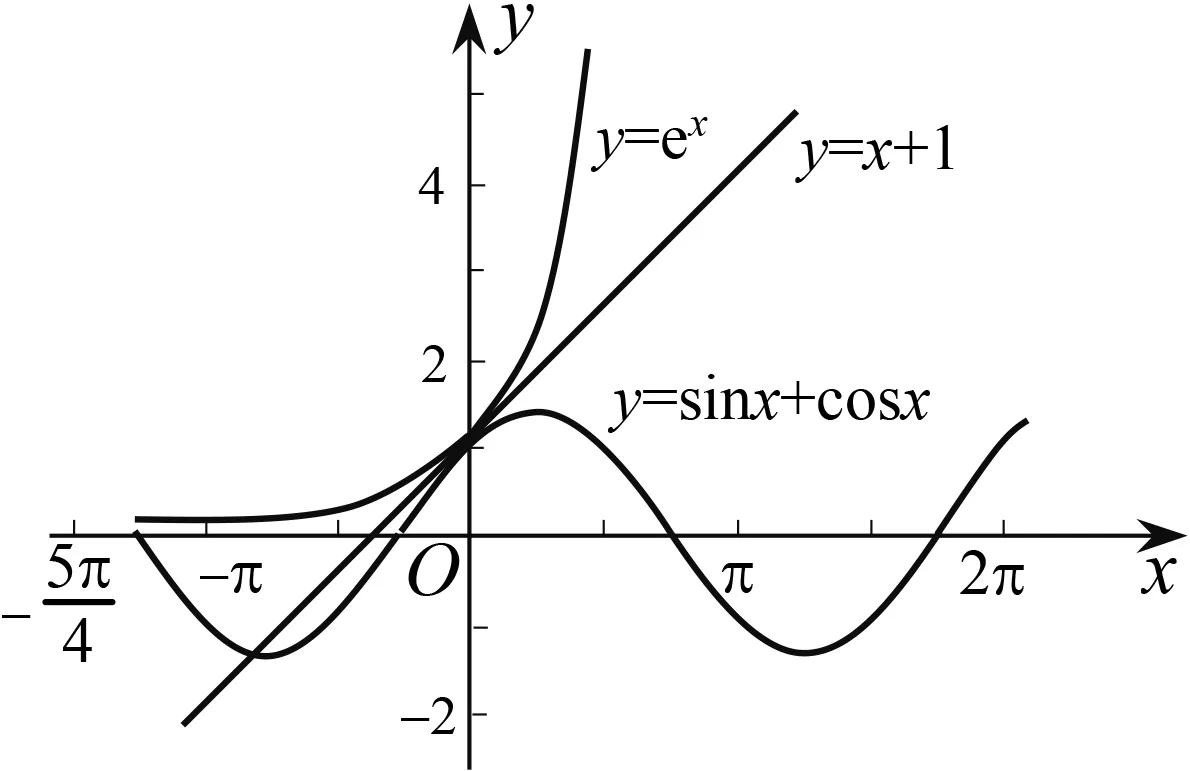
圖6

方法3：從結構角度表征

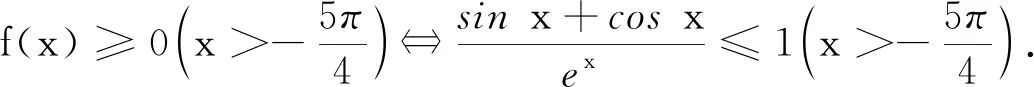
4 整體感悟，形成思維結構

研究表明，學生的思維都是從點狀階段逐步向線狀、網狀、結構狀階段發展．因此，在高三教學中，教師要想盡辦法拓寬思維空間，對學生孤立的、碎片的、零散的思維經驗進行整體的梳理、完善、建構，使知識、方法、思想不再是雜亂無章的堆積，而是有秩序、有層次、有系統的“串聯”，使學生形成結構化的思維，切實提高高三復習效果．

教學片段4問題：本節課你收獲了哪些基本知識？哪些基本技能？哪些基本思想？哪些基本活動經驗？

學生暢所欲言，教師逐層顯現思維結構圖(圖7)，使學生在大腦中建立起函數導數章節的體系，明確如何研究與三角函數有關的復雜函數的性質、在什么條件下直接研究函數的特征、在什么條件下用導數研究函數性質、如何用、有哪些主要的解題技巧、又蘊含著哪些思想，等等.通過學生基本活動經驗的匯集、思維結構圖的梳理，使學生能夠把“四基”內化于心，能夠做一題會一類通一片，逐步形成一種意識、觀念和素養，運用到后續的學習中去．

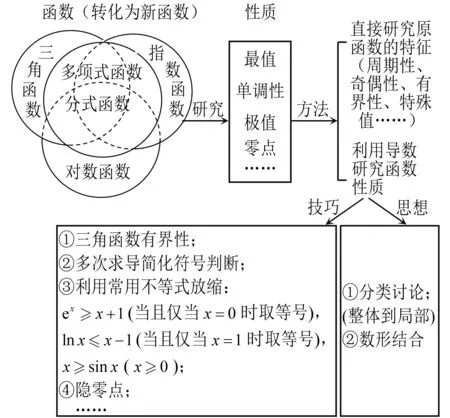
圖7

美國圖論專家哈里說：“千言萬語不及一張圖.”借助思維可視導引教學，可以讓隱性的思維變外化顯現、抽象的思維變形象可視、零散的思維變整體有結構.教師能更準確地把握學生思維的走向和水平，能讓學生認識數學知識的本質，理清數學方法之間的邏輯關聯，促進學生深度思考，不斷提升學生的學習力，更好地促進學生數學核心素養的形成.