考慮幾何公差的設計與工序公差并行分配研究*

彭和平

(武昌首義學院機電與自動化學院，武漢 430064)

0 引言

公差是產品設計、制造和檢驗中最重要的產品信息之一，是CAD/CAPP/CAM/CAQ不同環節之間數據交換和共享的主要內容之一。設計公差與工序公差的并行分配，對于產品性能質量和制造成本均具有很大的影響，公差已經成為平衡產品制造成本與性能質量的橋梁[1]。目前并行公差設計模型大部分基于制造成本和質量損失之和最小進行的尺寸公差的并行分配，并沒有考慮幾何公差，有一些研究考慮了幾何公差，但忽略了制造成本和產品滿意度之間的平衡[2-3]。本研究的目的是擴展并行公差設計模型以考慮幾何公差的要求。首先，在并行公差設計的環境下為了考慮幾何公差的影響，探討了幾何公差的轉化方法；在此基礎上建立并行設計與工序公差分配模型；最后，利用非線性規劃技術對模型進行求解，以獲得優化設計與工序公差值，實現包括幾何公差在內的并行公差分配。

1 幾何公差的轉換

幾何公差用于控制零件在形狀、方位、位置等方面的真實要素相對于理想要素或基準要素的變化。由于幾何公差對零件的性能和制造成本有著重要影響，因此在公差設計中考慮幾何公差是非常必要的，以滿足產品功能要求，保證零件互換性和制造的經濟性。根據ISO1101[4]，14種幾何公差被分為形狀、方向、位置和跳動4種類型。并非所有的幾何公差都可以轉化為等效的外部公差。與位置相關的幾何公差可以轉化為等效的外部公差；而形狀和方向公差僅僅指定局部特征，不能直接與線性尺寸耦合，它們將被視為額外的公差約束[5-6]。因此，在這14個幾何公差中，只有位置度、同心度、對稱度和輪廓度這4個公差直接影響工序公差鏈，可以轉化為等效的尺寸公差，其余的幾何公差項被建模為附加加工約束。

1.1 位置度公差

對于一個點的位置度公差，公差區域是直徑Sφt的球體，其中心由相對于基準位置的理論上精確尺寸確定。線的位置度公差可分為三種類型：①當線的位置度公差只指定一個方向時，公差區域由兩個間隔距離為T的平行平面組成的區域，并相對于所考慮的線的理論準確位置對稱布置。②當線的位置度公差指定在兩個相互垂直的方向上時，其公差區域為截面t1×t2的平行六面體，其軸線位于所考慮直線的理論準確位置。③當線的位置度公差在任意方向時，公差區域為直徑為T的圓柱體，其軸線與所考慮線的理論準確位置重合。在上述三種情況下，考慮線的理論精確位置取決于基準位置和理論準確尺寸。對于平面或中心平面的位置度公差，公差區域應包含在間隔距離為T的兩個平行平面之間，并相對于所考慮表面的理論準確位置對稱配置。

圖1表明如何將位置度公差轉換為可集成到公差鏈中的等效尺寸公差。如圖1中的孔相對于基準A和B的位置度公差為TP；等效線性尺寸公差在兩個互相垂直方向分別為±0.5Tp·cos45°和±0.5Tp·sin45°。因此，位置度公差的轉換模型可以表示為：

(1)

式中，X是理論上準確的尺寸，TP是位置度公差。

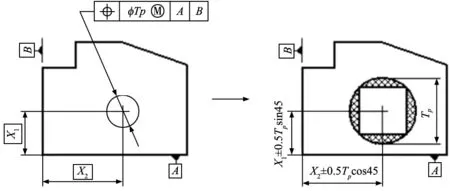
圖1 位置度公差的轉換

在此需要注意的是，如圖1所示位置度公差指定了最大材料要求，如果孔不在他們的最大實體狀態下，GD&T公差將被賦予額外的公差補償。此外，我們假設所有的尺寸公差都是相對于其名義尺寸的雙邊分布，并且我們在公差轉換過程中采用極值法。

1.2 同軸度公差

同心(軸)度公差是定位公差的一種，它是指關聯實際要素對具有確定位置的理想要素所允許的變動全量，用于控制被測要素對基準的同心(軸)性變動。理想要素的位置由基準確定。對于點的同心度公差，所提取的點應包含在一個直徑為T的圓內，圓心與基準點重合。對于軸的同軸度公差，所提取的軸應包含在軸線與基準軸線重合直徑為T的圓柱面內的區域。

圖2說明了同軸度公差如何轉換為兩個相互垂直軸上的等效線性尺寸和公差。

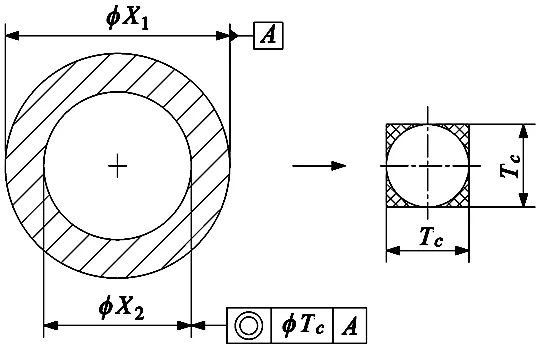
圖2 同軸度公差的轉換

并且相關工序公差的累計總和不應大于規定的同心度公差，也即：

(2)

式中，TC為同心度公差，Tji為與同心度公差相關的第i個工序尺寸xji的工序公差，p為相關工序尺寸的數量。

1.3 對稱度公差

對稱度公差也是一種定位公差，它是指關聯實際要素對具有確定位置的理想要素所允許的變動全量，用于控制被測要素對基準的對稱性變動，理想要素的位置由基準確定。

對于僅指定一個方向的對稱度公差，其公差帶為距離為公差值T，中心平面(或中心線、軸線)與基準中心要素(中心平面、中心線或軸線)重合的兩平行平面(或兩平行直線)之間的區域。如果對稱度公差指定在兩個相互垂直的方向上，則公差區域為截面t1×t2的平行六面體，其軸線與基準軸線重合。對稱度公差的轉換模型為：

(3)

式中，TS是對稱度公差，Tji為與對稱度公差相關的第i個工序尺寸xji的工序公差，p為相關工序尺寸的數量。

以圖3中所示的零件為例，對稱度公差的轉換模型為：

(4)

圖3 對稱度公差的轉換

1.4 其他幾何公差

其他幾何公差，比如：形狀公差(包括直線度、平面度、圓度、圓柱度等)、方向公差(包括平行度、垂直度、傾斜度等)和跳動公差，一般應作為公差設計模型中的附加約束。具體地說，這種類型的幾何公差的值不應該大于與引起這些幾何公差的加工表面相關的工序公差。不等式可以表示為：

TG≤Tji

(5)

式中，TG是幾何公差，Tji是與幾何公差相關的工序尺寸xji的雙向公差。

根據上述分析，幾何公差的轉換有些可以轉化為等效的尺寸公差，有些只能作為公差優化設計中的附加約束條件。

2 并行公差模型

本節對基于制造成本-期望質量損失的并行公差設計模型進行擴展，提出綜合考慮尺寸公差和幾何公差的并行優化分配方法。

2.1 成本-工序公差模型

產品制造成本與其公差之間存在著密切的聯系，國內外許多學者對成本-公差建模進行了研究。目前，比較成熟的成本-公差模型包括：指數模型、倒數平方模型、倒數冪指數模型、倒數冪和指數混合模型、指數和冪指數復合模型、倒數模型、離散模型、改進的指數模型、線性和指數復合模型、三次多項式模型、四次多項式模型等。假設在第i道工序中加工第j個零件特征到工序公差Tji的制造成本為：

cji=C(Tji),i=1,2,…,p;j=1,2,…,q

(6)

總的成本是每道工序加工制造成本之和，于是有：

(7)

式中，Cji(Tji) 是零件第j個特征的第i道加工工序的制造成本；q是零件特征數；p是第j個特征的加工工序數。

2.2 期望質量損失與工序公差函數關系

文獻[7]提出了被廣泛使用的二次質量損失函數。對于一個復雜的裝配，其功能要求由多個裝配特征確定。設產品第k個裝配尺寸zk(k=1, 2, …,r)是q個零件設計尺寸的函數：

zk=gk(y1,y2,…,yq)

(8)

式中，yj(j=1, 2,…,q)為第j個零件設計尺寸。

用Taylor級數展開式(8)并且略去二階及以上高次項，則裝配尺寸zk的偏差值為：

(9)

文獻[8]擴展了Taguchi的質量損失函數，提出了計算這些具有多重相關特征的產品質量損失的一般公式：

(10)

式中，Akl為質量損失系數。根據文獻[3]其期望質量損失為：

(11)

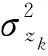
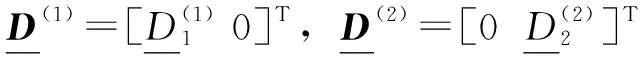
(12)

(13)

(14)

在產品設計階段，假設零件設計尺寸的變動是正態分布的，裝配尺寸的變動也為正態分布。根據統計理論，產品裝配尺寸參數的方差和協方差為：

(15)

(16)

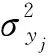
在工序公差設計階段，零件每個設計尺寸yj可表達為工序尺寸xji的函數(i=1, 2, …,p)。

yj=fj(xj1,xj2,…,xjp)

(17)

式中，xji是設計尺寸yj的第i步工序尺寸；p是與設計尺寸yj相關的加工工序總數。

在穩定加工條件下，假設所有的被加工尺寸xji是正態分布，類似地有：

(18)

(19)

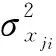
將式(18)和式(19)分別代入式(15)、式(16)和式(9)，有：

(20)

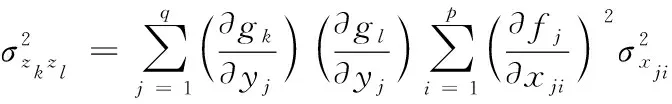
(21)

(22)

在一般正常生產的情況下，可以假定各組成環尺寸及公差服從正態分布，并假定各組成環尺寸及公差相對于公差帶中點呈對稱的正態分布，取零件的公差范圍為±3σ(σ為正態分布的標準偏差)對應零件的合格率為99.73%，則有：

(23)

式中，Tji是工序尺寸xji的雙向公差。

將式(23)代入式(20)、式(21)有：

(24)

(25)

將式(24)、式(25)代入式(11)，于是表示為工序公差Tji的函數形式的期望質量損失為：

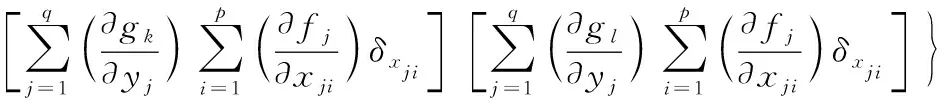
(26)

2.3 并行公差模型

在并行公差設計中，目標函數為產品的總成本，它是產品的制造成本與期望質量損失的和，各工序公差為待確定的設計變量。

目標函數

min{E[L(Tji)+MC(Tji)]}

(27)

式中，E[L(Tji)] 和MC(Tji)分別是產品的期望質量損失和總的制造成本。

約束條件

(1)基于WC(Worst-case)模型的并行公差累積約束

(28)

式中，Tzk為產品功能參數zk的公差極限上限。

(2)基于RSS模型的并行公差累積約束

(29)

(3)幾何公差要求的約束

如前節所述，只有位置度、同心度、對稱性度和輪廓公差可以直接轉化為等效的尺寸公差，其余的幾何公差項，如直線度、圓度、垂直度、平行度等，可視為附加加工約束，這些加工約束就是幾何公差不應該大于相關的工序公差。

(4)每道加工工序的經濟加工范圍約束

(30)

3 實例

根據該裝配的功能需求，可以識別出兩個關鍵的裝配尺寸鏈，如圖4所示，表示這兩個裝配尺寸鏈的方程分別為：

z1=-y1-0.5y2+0.5y3+y4

z2=-0.5y3-y5+y6+ypo+yco+y7

式中，ypo是由小孔垂直軸線相對于基準面A、C的位置度公差Tpo轉換而來的等效公稱尺寸；yco是大孔軸線相對基準軸線B的同軸度公差Tco轉換而來的等效公稱尺寸。

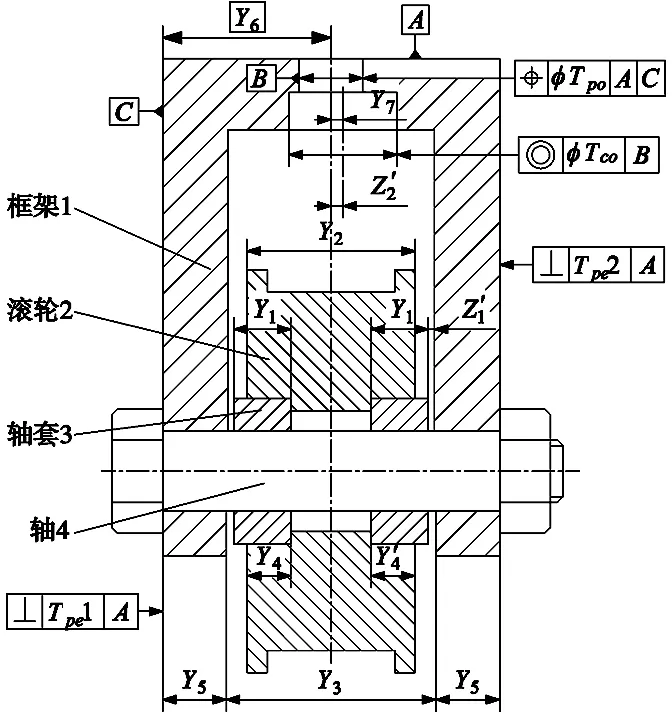
圖4 滾輪裝配

圖5～圖7所示為裝配中關鍵零件框架1、滾輪2、軸套3的加工順序，表1列出了這3個零件的加工工序規劃。根據式(9)，我們有：

δz1=-δy1-0.5δy2+0.5δy3+δy4

δz2=-0.5δy3-δy5+δy6+δypo+δyco+δy7

根據圖5～圖7和表1給定的各個零件的加工工序，可以獲得下列加工方程：

y1=x32-x33

y2=x24

y3=x15-x16-x17

y4=x25

y5=x17

y6=x18=40

y7=x19-x18=0

于是，根據式(24)和式(25)有：

圖5 框架1的加工順序

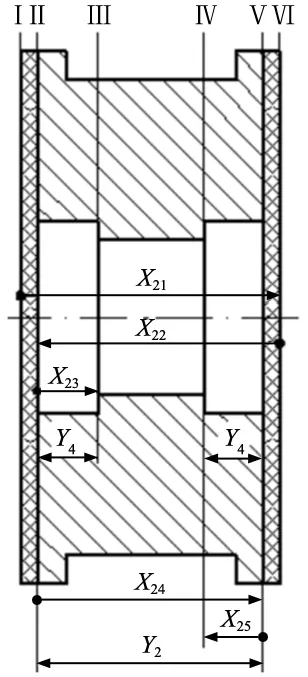
圖6 滾輪2的加工順序

圖7 軸套3的加工順序

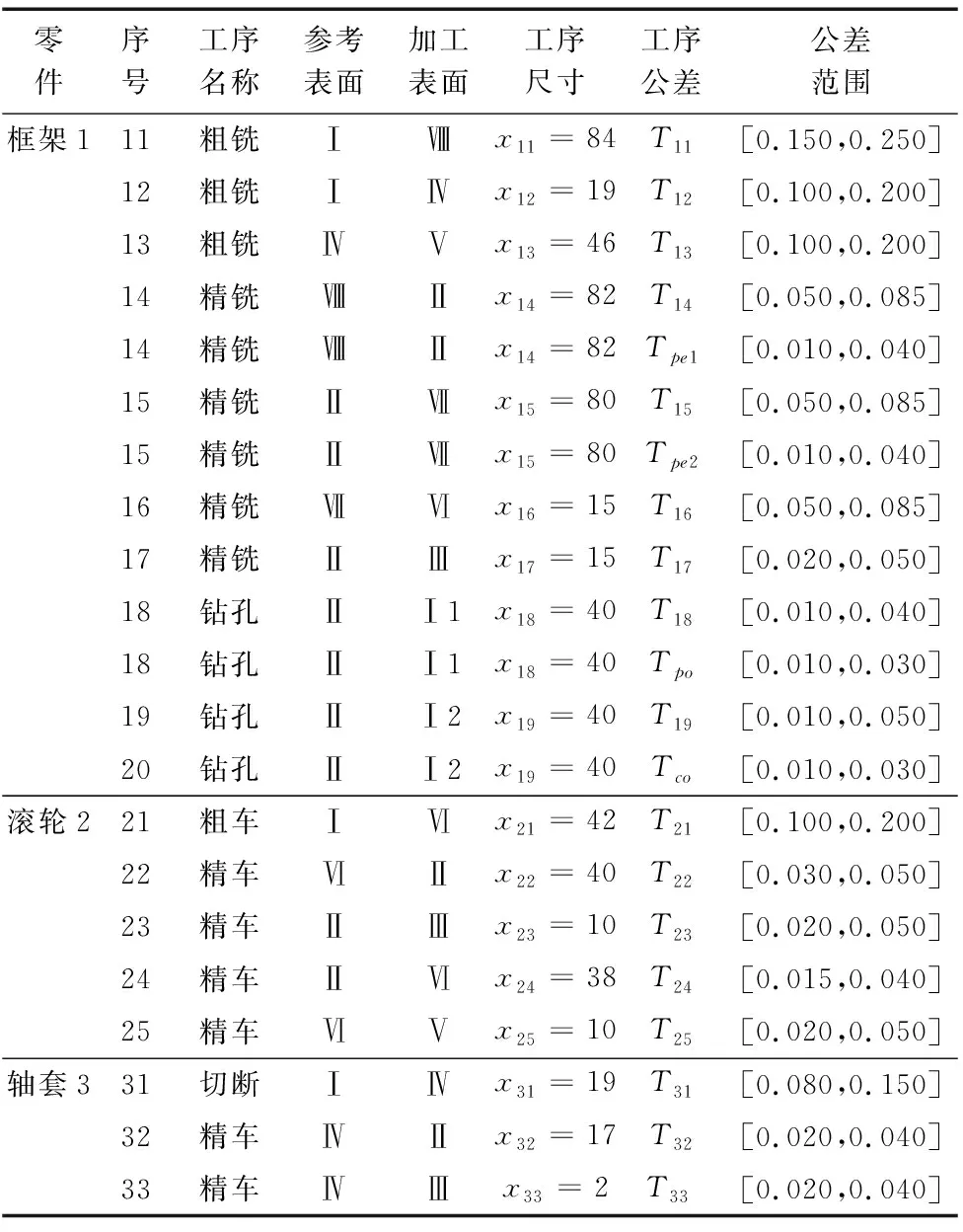
表1 框架1、滾輪2、軸套3的加工工序 (mm)

表1中，Tpo、Tco分別為框架1的小孔軸線相對于基準面A、C的位置度公差和大孔軸線相對基準軸線B的同軸度公差；Tpe1和Tpe2分別是框架1的左、右兩平面相對于基準平面A的垂直度公差。

在穩定生產條件下，假設各工序尺寸分布中心值與其目標值重合，在此忽略其偏差對期望質量損失的影響，根據式(26)期望質量損失表達式為：

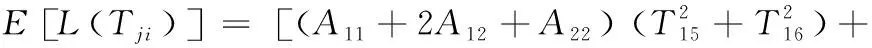
注意：本例僅考慮由于與裝配功能要求相關的工序尺寸的變動所引起的期望質量損失。對其他工序尺寸使用最經濟的公差值，這些工序尺寸的變動對質量損失沒有貢獻，同樣的考慮也應用于制造成本。

本例制造成本模型采用由文獻[10]提出的倒數冪和指數混合模型，根據該模型零件第j個設計參數通過第i道工序獲得工序公差Tji的制造成本由下式確定：

式中，參數a0,a1,a2,a3,a4可以用最小二乘近似法確定。根據文獻[10]的研究：

對于孔加工：

對于平面銑削：

對于車削：

根據式(7)，本例的制造成本為：

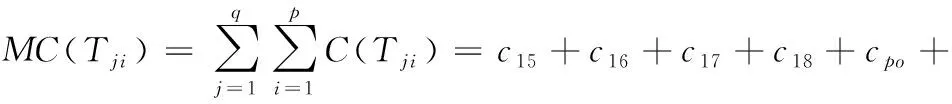
式中，

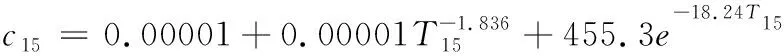
在并行設計的環境下，綜合期望質量損失和總的制造成本，可以得到并行公差優化模型：

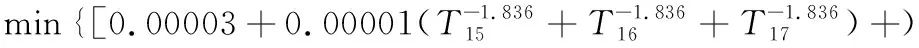
考慮約束條件包括產品功能約束、幾何公差要求約束、加工工序的經濟加工范圍約束等。

(1)產品功能約束：

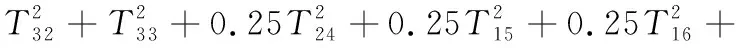
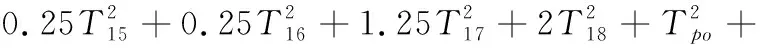
(2)幾何公差約束：

T18-0.5Tpo·cos45°≤0
T18+T19-Tco≤0
Tpe1-T14≤0
Tpe2-T15≤0

(3)經濟加工工序邊界約束 ：

0.050≤T14≤0.085，0.010≤Tpe1≤0.040
0.050≤T15≤0.085，0.010≤Tpe2≤0.040
0.050≤T16≤0.085，0.020≤T17≤0.050
0.010≤T18≤0.040，0.010≤Tpo≤0.030
0.010≤T19≤0.050，0.010≤Tco≤0.030
0.015≤T24≤0.040，0.020≤T25≤0.050
0.020≤T32≤0.040，0.020≤T33≤0.040

本例采用非線性規劃技術求解該模型，獲得優化工序公差和相關設計公差見表2和表3。

表2 優化工序公差

表3 優化設計公差

4 結束語

并行公差設計模型將產品設計階段和零件加工階段結合起來，實現了零件工序公差和設計公差的同步分配，可以保證產品的可制造性，提高設計效率，降低整體生產成本，減少不合格產品數量，縮短產品開發周期。本研究基于幾何公差的數學表達，進一步將并行公差設計模型擴展到考慮幾何公差要求。具體方法是：與位置特征相關的幾何公差可以轉換為等效尺寸公差；與形狀或方向特征相關的其他幾何公差被視作幾何約束，然后將等效尺寸公差或幾何約束集成到并行公差設計模型中，從而在該模型中考慮幾何公差要求。最后，利用非線性優化技術，將期望質量損失和制造成本之和最小化，同時得到優化的設計和工序公差。下一步的研究將該模型擴展到同時包含多個尺寸和幾何公差的復雜特征，以及含有幾何公差原則的公差并行分配問題等。