基于改進遺傳算法的磨削能耗預測及工藝參數優化*

李 陽，劉儼后，張 昆，田業冰，田承金

(山東理工大學機械工程學院，山東 淄博 255000)

0 引言

磨削作為應用最廣泛的精密與超精密加工方式之一，其表面加工質量和能耗是當前關注的熱點，國內外學者針對磨削表面粗糙度和磨削能耗進行了一系列研究。文獻[1]對表面粗糙度測量理論與技術方法發展的現狀進行了全面概述；文獻[2]依據進化神經網絡構建了磨削粗糙度的預測模型；文獻[3]建立了砂輪線速度、工件進給速度與磨削深度對工程陶瓷內圓表面粗糙度的經驗公式；文獻[4]從分析方法的角度對表面粗糙度預測與建模的研究進展進行了綜述；文獻[5]研究了磨粒葉序排布與磨削表面粗糙度關系，證明葉序系數與表面粗糙度呈正相關；文獻[6]構建了非圓磨削過程中工件上所受扭矩的計算模型和磨削能耗計算模型；文獻[7]以銑削加工過程中的切削能耗、加工質量以及加工效率作為優化目標，采用灰色關聯法進行尋優；文獻[8]用BP神經網絡預測附加載荷系數，間接預測出數控磨床磨削能耗。

上述研究在建立表面粗糙度或磨削能耗的預測模型方面取得一些成果。但是，以往只是單方面對表面粗糙度預測模型或磨削能耗預測模型進行研究，而將表面粗糙度與磨削能耗的預測模型有效地結合起來進行磨削工藝參數優化的研究卻很少。本文在建立的表面粗糙度和磨削能耗的預測模型基礎上，以保證表面粗糙度滿足一定加工要求為前提，求磨削能耗的最小值為目標，設計了一種改進遺傳算法，基于磨削能耗預測進行磨削工藝參數優化。

1 工藝實驗

1.1 設備條件

在SMART-BB18III型高精度平面磨床上進行磨削實驗，采用白剛玉砂輪，砂輪直徑200 mm，實驗材料45號鋼，尺寸50×50×25 mm，加工50×50 mm的表面。使用功率分析儀獲取磨削加工過程總能耗，采用TIME3200粗糙度測量儀測量磨削加工后的工件表面粗糙度。

1.2 實驗設計

磨削用量參數選取：砂輪線速度vs(m/min)、工件進給速度vw(mm/min)和磨削深度αp(μm)。vs、vw和αp分別取5個水平，具體如表1所示。

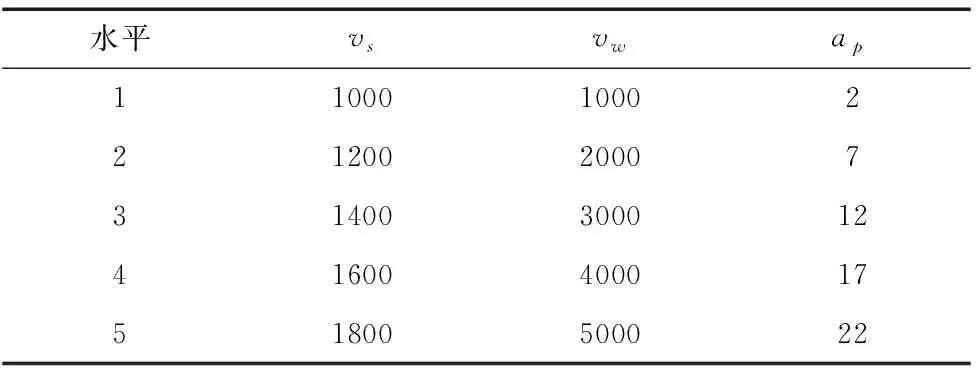
表1 磨削工藝參數

實驗結果如表2所示。

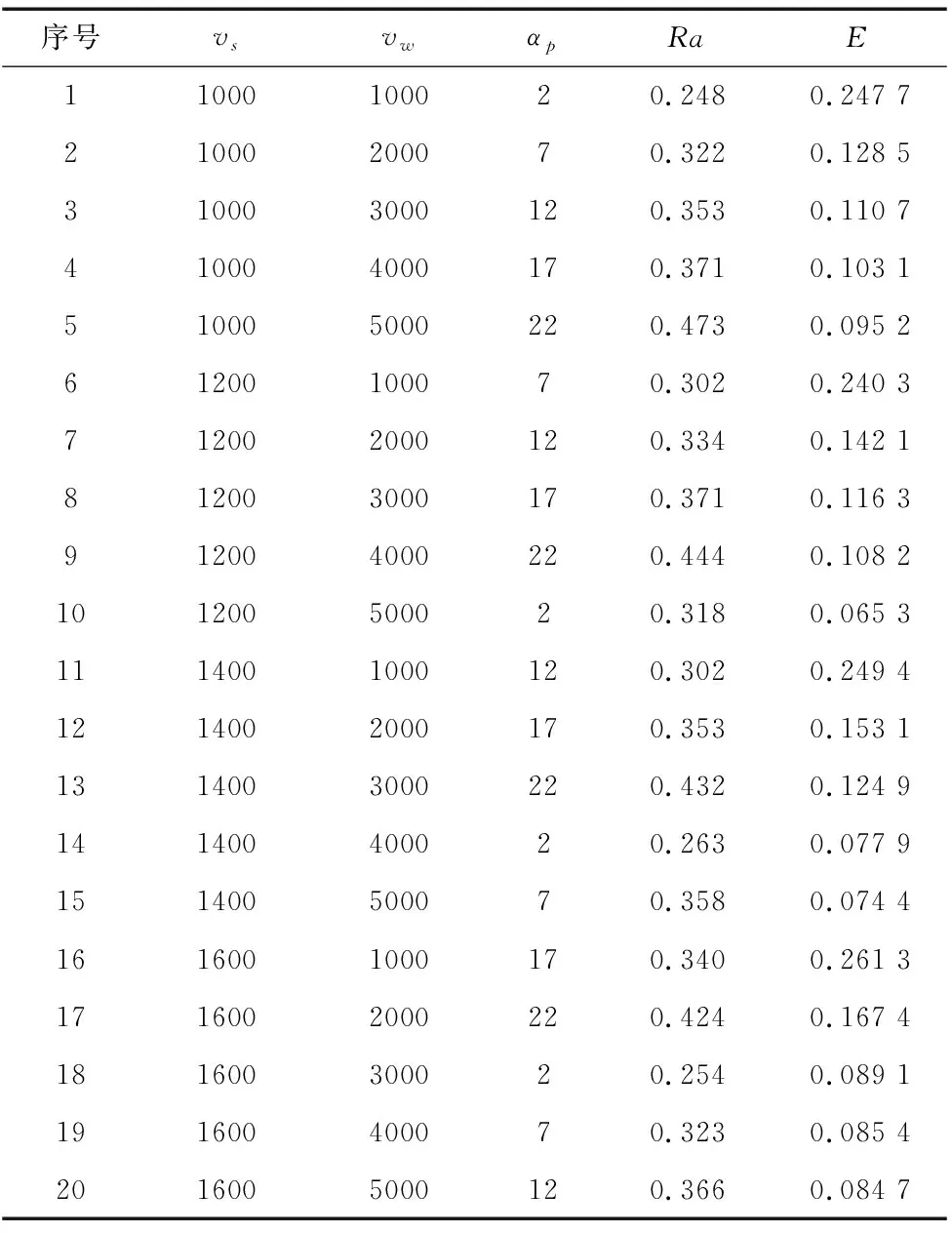
表2 磨削實驗數據結果

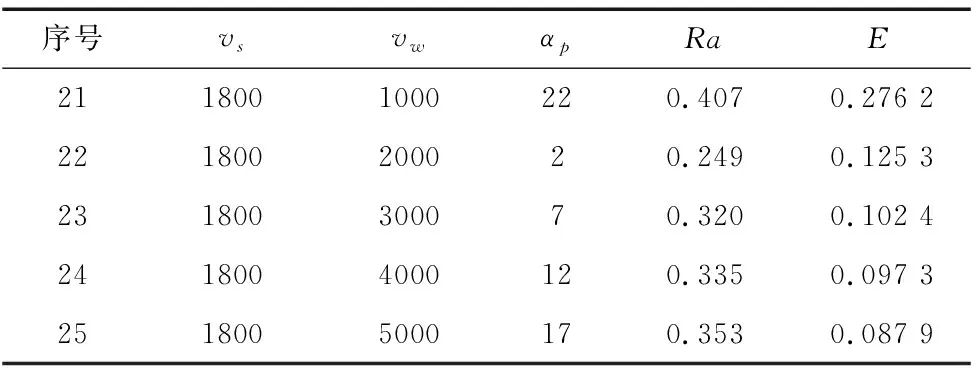
續表

2 表面粗糙度和磨削能耗預測模型

2.1 建立數學模型

根據多元非線性回歸方法，將砂輪轉速vs、工件進給速度vw和磨削深度αp設置為獨立變量，表面粗糙度Ra和磨削能耗E設置為因變量。采用多元非線性冪函數數學模型進行構建。

(1)

(2)

其中，λ、β、η和α均為各自對應多元非線性數學模型的參數。分別對式(1)和式(2)兩邊作對數變換，可得到式(3)和式(4)：

lgRa= lgλ+β1lgvs+β2lgvw+β3lgαp

(3)

lgE= lgη+α1lgvs+α2lgvw+α3lgαp

(4)

上述公式的多元線性回歸方程可以寫成下列形式：

y1=β0+β1x1+β2x2+β3x3

(5)

y2=α0+α1x1+α2x2+α3x3

(6)

式(5)中，y1=lgRa，β0=lgλ，x1=lgvs，x2=lgvw，x3=lgαp，式(6)中，y2=lgE，α0=lgη，x1=lgvs，x2=lgvw，x3=lgαp。

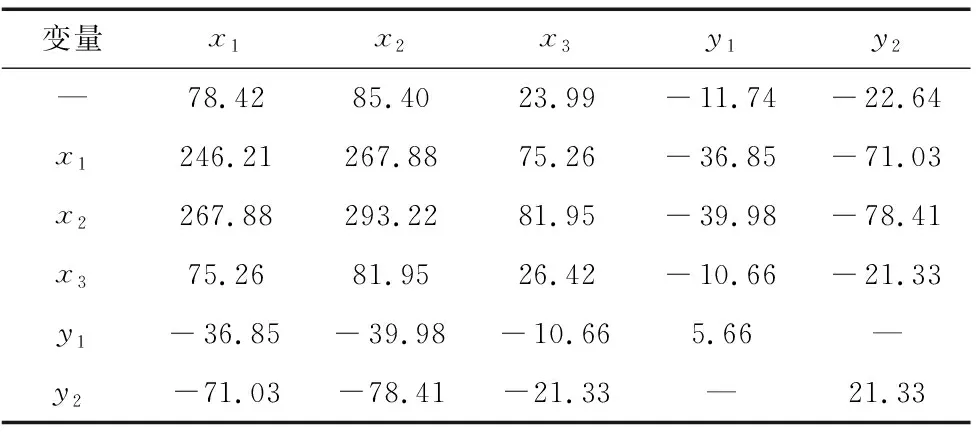
表3 統計數據計算結果

由一級統計數據計算二級統計數據如下：

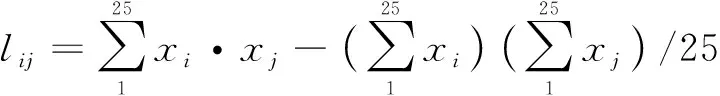
l11=0.204,l22=1.524,l33=3.405,
l12=-1.929×10-8=l21,ly1y1=0.143,
l13=-1.406×10-8=l31,lx1y1=-0.021,

l23=-1.893×10-8=l32,lx2y1=0.131,
lx3y1=0.610,ly2y2=0.828,lx1y2=-0.008,
lx2y2=-1.080,lx3y2=0.394。

，

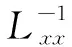
故式(5)的經驗回歸方程可以寫成：

y1=-0.61-0.103x1+0.086x2+0.179x3

(7)

故式(6)的經驗回歸方程可以寫成：

y2=1.533-0.041x1-0.709x2+0.116x3

(8)

2.2 多元非線性擬合方程的檢驗與偏回歸系數的檢驗

計算回歸平方和Uy1、Uy2，剩余平方和Qy1、Qy2，x對y的方差貢獻Uy11、Uy12、Uy13和Uy21、Uy22、Uy23并進行檢驗。

Uy1=β1·lx1 y1+β2·lx2y1+β3·lx3y1=0.123，
Uy2=α1·lx1y2+α2·lx2y2+α3·lx3y2=0.811，

Qy1=ly1y1-Uy1=0.021，
Qy2=ly2y2-Uy2=0.017，

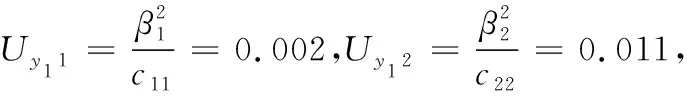
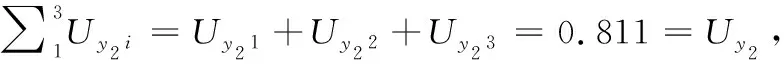
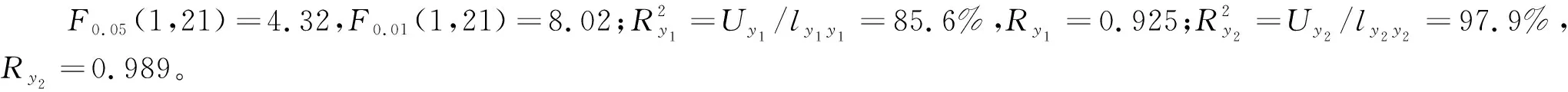
(9)

(10)

3 預測模型有效性驗證

為驗證預測模型的有效性，設計五組磨削參數組合進行對比分析，其中T表示實驗值，P表示預測值，預測值與實驗值對比結果如表4所示。

表4 磨削實驗數據結果

經計算知五組磨削實驗中，磨削用量與表面粗糙度的多元非線性方程式的平均絕對誤差為1.84%，磨削用量與磨削能耗的多元非線性方程式的平均絕對誤差為0.78%。因此式(9)、式(10)所示預測模型具有較高的預測精度。

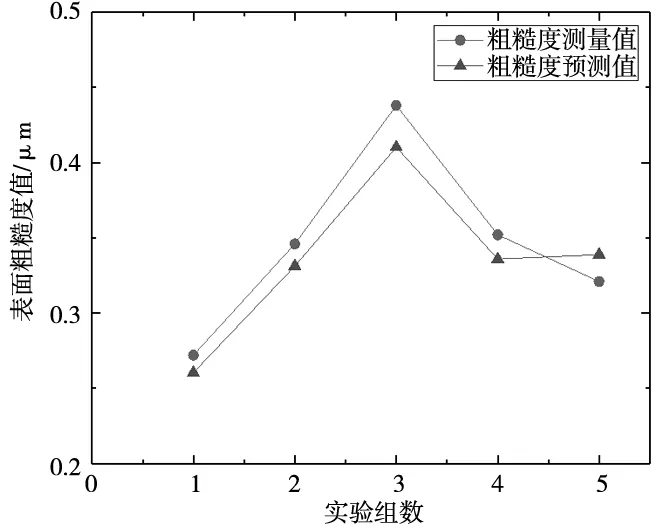
圖1 實測粗糙度與預測粗糙度比較

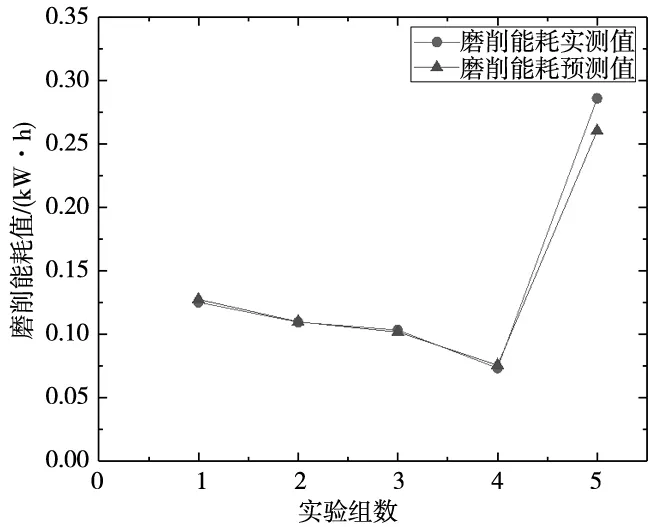
圖2 實測磨削能耗與預測磨削能耗比較

4 基于預測模型的工藝參數優化

4.1 改進遺傳算法

本文以式(10)所示預測模型為目標函數，式(9)所示預測模型為約束條件，設計了一種改進遺傳算法(Improved Genetic Algorithm, IGA)，進行磨削工藝參數優化。

4.1.1 優化模型目標函數及約束條件

將式(9)的多元非線性方程式轉化為不等式約束條件，遺傳算法求解磨削能耗最小值進化過程知，每一代的表面粗糙度都不超過0.36 μm，為保證產生的初始種群和進化過程中產生的種群存活率，在式(9)的基礎上減去0.36 μm，表示在滿足表面粗糙度小于0.36 μm的前提下，求磨削能耗最小值。將式(10)的多元非線性方程式轉化為目標函數，優化模型為：

minF(x,y,z)=34.132·x-0.041·y-0.709·z0.116

(11)

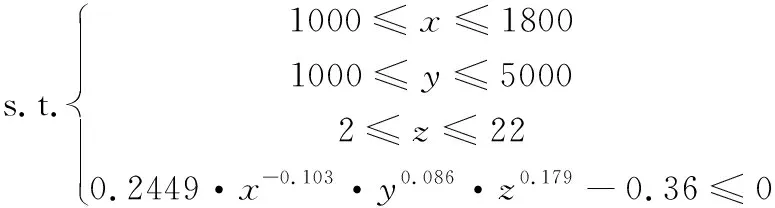
其中，x，y，z均為決策變量。

取目標函數的倒數作為適應度函數。

f(x,y,z)=1/34.132·x-0.041·y-0.709·z0.116

(12)

4.1.2 編碼解碼

染色體編碼方式是遺傳算法需要解決的首要問題[9]。考慮到決策變量取值大、范圍大的特點，不宜采用一般的傳統二進制編碼方式，本文采用十進制編碼方式。十進制編碼中,設計每個決策變量占據4位基因，一個染色體的基因長度為12位，表示在滿足約束條件下工藝參數的一組可行解。在十進制編碼下,染色體中每個位置的基因都隨機出現0～9之間的一個數字，但是編碼后的染色體取值與實際決策變量區間范圍不符，因此需要對十進制編碼下的染色體進行解碼。假設某一決策變量的取值范圍為[L,U]，使用長度為n的十進制編碼表示該參數，則共有10n種不同的編碼方式，設某一個決策變量的十進制編碼為bnbn-1…b1，則對應的解碼格式為：

(13)

具體編碼解碼實例見圖3。

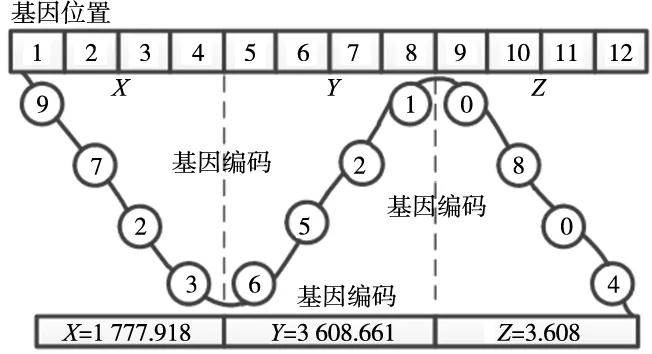
圖3 編碼與解碼

4.1.3 選擇算子

選擇算子是從初始種群中選擇適應度高的染色體，從而進行后續的交叉、變異算子操作。適應度函數作為衡量一個個體是否足夠“好”的重要標準，也有其弊端，因為一個種群中最優物種不一定是在全局最優點附近。故應該給相對適應度較低的個體一些機會讓其繁衍后代，以避免“早熟”。使用輪盤賭選擇策略，即種群中的染色體被選中概率與染色體相應的適應度函數值成正比[10-11]。將種群中所有個體的適應度值進行累加然后歸一化，最終通過隨機數對隨機數落在的區域進行對應的個體選取。

4.1.4 交叉算子

交叉算子在選擇算子選出的種群中，隨機選取兩個染色體，以某一概率互換兩個染色體中的部分基因，從而保證種群向著最優解進化。這里采用單點交叉，并隨機生成一個(0，1)上的數，若小于交叉概率則進行交叉操作，否則不進行交叉操作。具體交叉實例見圖4。

圖4 改進遺傳算法交叉操作

4.1.5 變異算子

變異算子可以使種群中染色體的基因多樣化，在單個染色體的某些位置進行變異[12]。基于研究的需要，這里選擇三點變異，具體操作為在十進制染色體上，前四位、中間四位和后四位各產生一個變異點，變異范圍為0～9之間任意一個整數(圖5)。變異評判標準是隨機生成一個(0，1)上的數，與變異算子發生概率進行比較，若小于變異概率則進行變異操作，否則不進行變異操作。

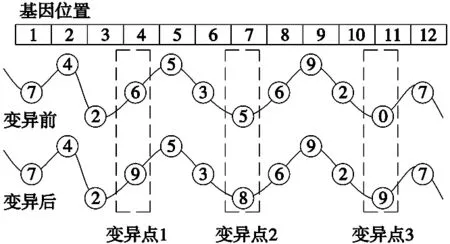
圖5 改進遺傳算法變異操作

4.1.6 改進遺傳算法的流程(圖6)

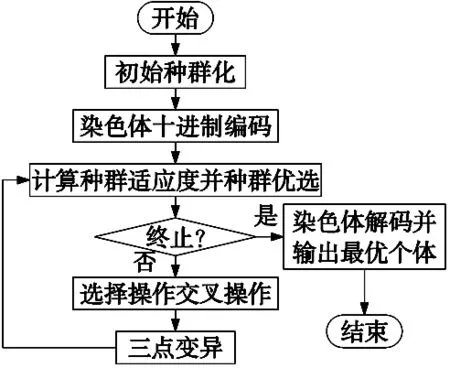
圖6 改進遺傳算法流程

4.2 二進制與十進制編碼下的測試結果

4.2.1 改進遺傳算法參數設置

經進化迭代結果知，設置初始染色體數目為100，迭代次數為70，交叉概率為0.8，變異概率為0.003時工藝參數優化效果最為理想。由初始染色體數目為100，染色體基因長度為12位，知創建的初始種群為100×12的矩陣。

4.2.2 改進遺傳算法求解結果對比

遺傳算法中，分別使用二進制編碼單點變異和十進制編碼三點變異的編程方式，通過進化迭代次數可知，兩種方法最終收斂精度在0.066 kW·h附近。采用常規二進制編碼單點變異進化迭代次數需要100代，采用改進遺傳算法只需迭代70次，改進遺傳算法迭代次數更少。而同樣迭代100次的情況下，常規二進制編碼單點變異系統程序運行需要時間4.6 ms，改進遺傳算法系統運行需要時間3.9 ms，明顯改進遺傳算法速度更快。采用傳統遺傳算法中的二進制編碼方式，在二進制向十進制解碼的過程中，存在進化迭代緩慢、收斂速度緩慢的缺陷，本文采用的十進制編碼與解碼方式，可避免這一缺陷。兩種迭代比較見圖7。

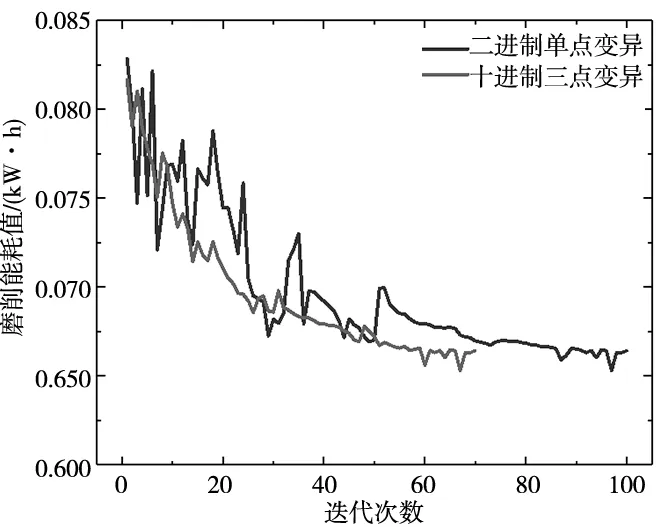
圖7 二進制與十進制編碼收斂迭代比較

4.2.3 求解結果分析

同樣進化迭代70次的情況下，常規遺傳算法下進化結果顯示砂輪線速度為1 731.233 m/min，工件進給速度為4 945.299 mm/min，磨削深度為3.021 μm時，表面粗糙度值為0.286 μm，磨削能耗值為0.068 8 kW·h；改進遺傳算法進化結果顯示砂輪線速度為1 792.773 m/min，工件進給速度為4 862.271 mm/min，磨削深度為2.015 μm時，表面粗糙度值為0.266 μm，磨削能耗值為0.065 3 kW·h。實驗環境不變的條件下進行磨削實驗，將常規遺傳算法和改進遺傳算法優化出的工藝參數分別作為磨床輸入，得到的實驗結果如表5所示。所示經計算知，表面粗糙度的精度提高了75%，磨削能耗的精度提高了22.2%。改進遺傳算法下的工藝參數優化結果與所做30組磨削實驗一一進行對比可知，改進遺傳算法優化出的工藝參數在滿足一定表面粗糙度的情況下，實現了磨削能耗的最小值，完成了工藝參數實質性的優化，達到了節約能源的目標。

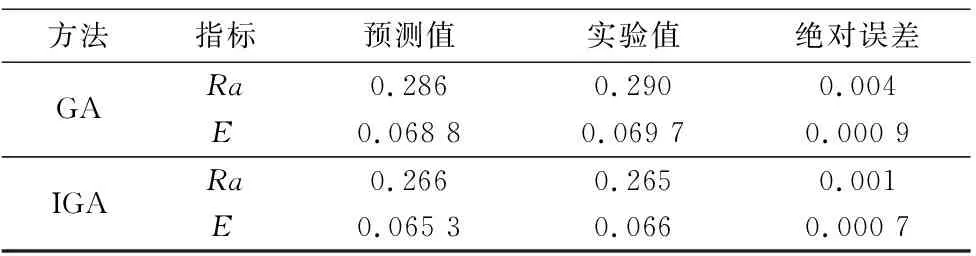
表5 磨削實驗數據結果對比分析

5 結束語

通過多元非線性擬合回歸法建立了磨削工藝參數與表面粗糙度和磨削能耗的多元非線性方程式。遺傳算法中使用十進制編碼解碼和三點同時變異的方式，提高了進化迭代速度與收斂精度。從結果驗證可知，復雜的磨削加工過程中，通過建立表面粗糙度和磨削能耗的多元非線性方程式，將兩個方程式作為改進遺傳算法中的約束條件和目標函數，可實現磨削工藝參數的優化。