基于改進MF-DFA的零件特征提取與缺陷識別*

何 濤，王 幸，王少東，王正家，盛文婷

(湖北工業大學 a.機械工程學院；b.現代制造質量工程湖北省重點實驗室，武漢 430068)

0 引言

零件作為工業制造領域中最基本的組成單元，其質量在工業制造領域中有著決定性的影響[1]。零件缺陷識別是實現產品質量檢測的至關重要環節，保證產品質量對制造業的發展有著舉足輕重的作用。由于在眾多機械零件中諸如齒輪這類環形零件呈現非線性、不規則和一定自相似性的特點，使得傳統檢測工具很難準確識別零件缺陷。因此，探索一種有效的零件缺陷識別方法，以滿足產品質量檢測的需求。

分形理論作為一門新興的非線性學科，適用于自然界中不規則事物的分析和處理。隨著科學技術的發展，分形理論在圖像處理中已取得廣泛的應用和一系列的成果[2]。單分形方法僅用單一維數來描述目標物體的特征，不能完整地刻畫其復雜性。文獻[3]提出了多重分形理論，即利用廣義維數與多重分形譜來描述客觀物體。文獻[4]在去趨勢波動分析法(DFA)的基礎上提出了多重分形去趨勢波動分析(Multifractality Detrended Fluctuation Analysis,簡稱MF-DFA)，該方法避免了人為因素的影響，能夠更準確地刻畫隱藏在非平穩時間序列中的多重分形特征，可較大幅度提高目標物體的識別準確度[5]，目前該方法已經應用到各領域。文獻[6]應用二維MF-DFA法計算糖尿病人的視網膜病變圖像的局部廣義Hurst指數，再將Hurst指數作為LSSVM中的訓練輸入量，對視網膜圖像進行檢測和分類識別，提高了圖像識別的靈敏性和準確性。文獻[7]引入滑動窗口技術對傳統MF-DFA算法進行改進，計算液壓泵的多重分形譜參數，最終利用半監督馬氏距離模糊C均值法實現了液壓泵退化狀態的識別。

傳統二維MF-DFA法存在過度覆蓋的問題，因此本文提出一種基于改進MF-DFA的零件圖像特征提取與缺陷識別研究方法。首先利用改進MF-DFA法計算預處理后的正常與缺陷齒輪圖像的多重分形譜；然后選擇多重分形譜中缺陷特征較為明顯區域的數據，通過核化主成分分析法(Kernelized Principal Component Analysis，簡稱KPCA)從中獲取齒輪圖像的缺陷特征值；最后利用支持向量機(Support Vector Machines，簡稱SVM)實現齒輪缺陷識別。

1 多重分形去趨勢波動分析

以多重分形算法為基礎的多重分形去趨勢波動分析算法得到了廣泛應用，可用在二維以及高數位序列[8]。對于齒輪和軸承這類環形零件，需要使用二維多重分形去趨勢波動分析(MF-DFA)法，能更全面刻畫零件圖像的信息，進而可以挖掘更顯著的多分形特征。對MF-DFA法進行改進，提出三角覆蓋的二維MF-DFA算法，可更精確地計算零件圖像數據的多重分形譜，并高效地進行多重分形特征分析。

1.1 二維MF-DFA理論

當q≠0時，測度波動函數Fq(s)為：

(1)

當q=0時，測度波動函數Fq(s)為：

(2)

(a) 覆蓋順序1(b)覆蓋順序2

(c) 覆蓋順序3(d)覆蓋順序4圖1 二維MF-DFA覆蓋順序

不斷改變正方形模塊的邊長s，得到一組不同尺度s下的測度波動函數Fq(s)，再將log(s)和log(Fq(s))進行線性擬合運算得到廣義Hurst指數h(q)，最后將其帶入式(3)中計算奇異指數α與奇異譜f(α)，即可得到序列x(m,n)的多重分形譜。

(3)

1.2 三角覆蓋的二維MF-DFA

在二維MF-DFA算法中，雖然使用正方形模塊計算獲得零件的多重分形譜較簡便，但是該方法容易造成過度覆蓋問題，導致計算結果不夠準確。對比圖2和圖3可知，三角形模塊覆蓋圖形輪廓曲線只計算不為零的模塊部分，取得的覆蓋輪廓比正方形模塊覆蓋輪廓更貼切地表達圖像輪廓的本質。采用正方形模塊覆蓋輪廓曲線內的面積占整幅圖像總面積的73.44%，而采用三角形模塊覆蓋相同輪廓曲線內的面積占圖形總面積的61.33%。故可知三角形覆蓋方法在保證圖像完全覆蓋的情況下，較好的解決了過度覆蓋的問題，提高了圖像覆蓋的精確度。因此，本文引入三角形模塊覆蓋法替換傳統正方形模塊覆蓋法，使用三角覆蓋的二維MF-DFA分析目標圖像的特征。

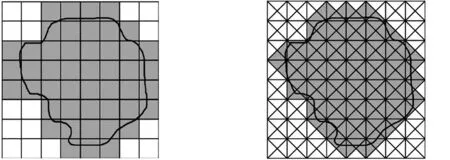
圖2 正方形覆蓋輪廓 曲線圖像 圖3 三角形覆蓋輪廓 曲線圖像

眾所周知，二元多項式擬合運算的復雜度比一元一次多項式擬合運算的復雜度更高[9]。因此，本文的三角覆蓋二維MF-DFA法選用一元一次多項式擬合來計算圖像測度波動函數Fq(s)。具體流程如下所示：

(1)對一幅大小為M×N的圖像x(m,n)構造去均值的和序列Y(i,j)。

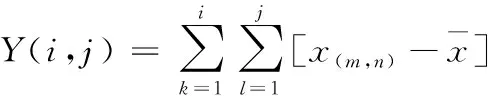
(4)

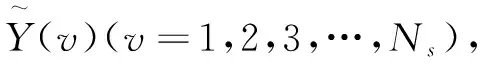
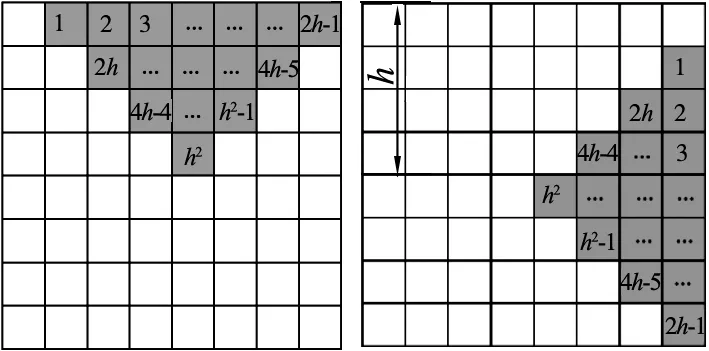
(a) 模塊1 (b)模塊2

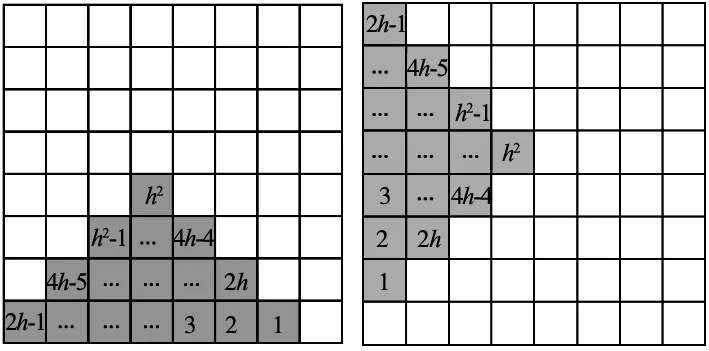
(c) 模塊3 (d)模塊4圖4 三角形覆蓋模塊

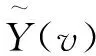
yv(k)=a1k+a2;k=1,2,...,s

(5)

(4)計算均方誤差F2(s,v)

(6)

(5)對于Ns個小區間，求其F2(s,v)的均值，并計算q階波動函數Fq(s)。

當q≠0時，測度波動函數Fq(s)為：

(7)

當q=0時，測度波動函數Fq(s)為：

(8)

(6)重復第(5)步，不斷改變等腰三角形模塊高h的數值，獲得一組不同h值下的測度波動函數Fq(s)，對s和Fq(s)分別取對數得到log(s)和log(Fq(s))。將兩者進行線性擬合得到廣義Hurst指數h(q)，并帶入式(3)中計算其對應的奇異指數α和奇異譜f(α)得到目標圖像的多重分形譜。

2 齒輪圖像特征值提取

2.1 齒輪多重分形特性分析

如果直接對系統采集的圖像進行廣義Hurst指數h(q)計算，圖像的背景區域和噪音光斑會對最終的計算結果造成影響。故在計算廣義Hurst指數h(q)前需對圖像進行預處理，即將采集的齒輪圖像經過二值化、面積濾波、背景區域灰度值還原以及零件區域灰度值取反處理后，零件圖像區域的特征被完整保留，如圖5所示。

(a) 正常齒輪預處理圖像 (b)缺齒齒輪預處理圖像圖5 齒輪零件預處理圖像

齒輪這類零件的圖像具備分形特性，判斷這類零件圖像是否滿足多重分形的特征，需要計算這類零件圖像的廣義Hurst指數h(q)，當對應的h(q)值隨著q的變化而變化時，齒輪零件圖像才具有多重分形特性。使用三角覆蓋二維MF-DFA算法對經過預處理后的齒輪圖像進行分析和計算得到其廣義Hurst指數h(q)，其中q值范圍為-13.5～+13.5，取值間隔為0.1。計算結果如圖6所示，其中q值為橫坐標，廣義Hurst指數h(q)值為縱坐標，可以觀察到正常與缺陷齒輪圖像的h(q)均隨著q值的改變而顯著變化。據此可知正常與缺陷齒輪圖像具有多重分形特性，并用多重分形譜對其進行特征分析。

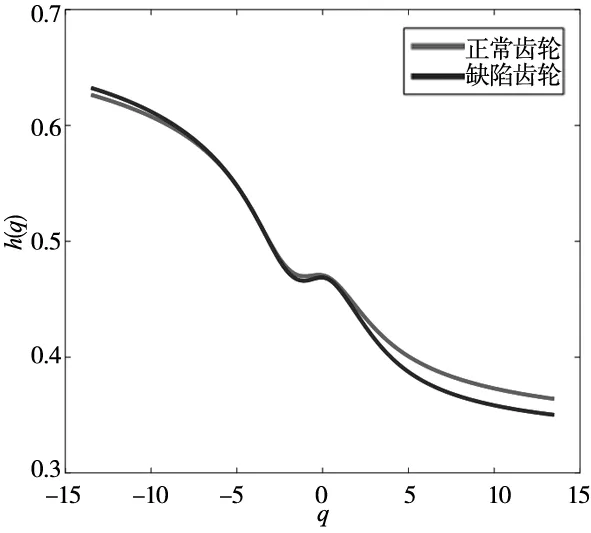
圖6 正常與缺陷齒輪零件預處理圖像Hurst指數h(q)

2.2 齒輪圖像多重分形譜計算及其缺陷分析

使用三角覆蓋的二維MF-DFA算法分別對正常與缺陷齒輪圖像進行多重分形譜的計算，計算結果如圖7所示，圖中橫坐標為奇異指數α，縱坐標為對應的奇異譜f(α)。

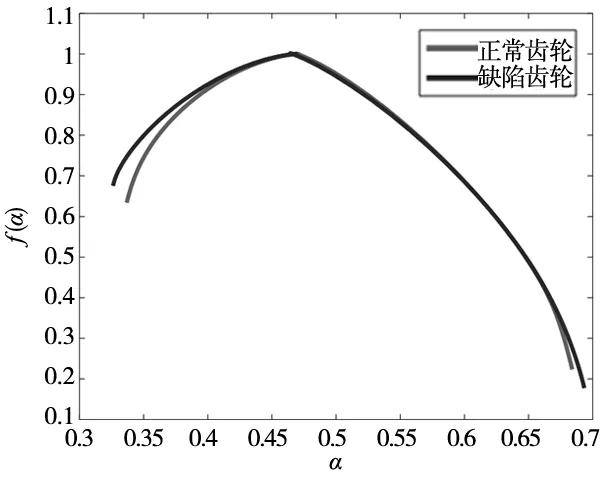
圖7 正常與缺陷齒輪圖像的多重分形譜

單張齒輪圖像的多重分形譜不能充分詮釋齒輪零件圖像的整體特征。為了得到齒輪零件最具代表性的特征值，采集正常與缺陷齒輪在不同位置狀態下的圖像各20張，分別計算這些圖像的多重分形譜，將計算好的20張正常齒輪零件圖像的多重分形譜與其對應的20張缺陷齒輪的多重分形譜以不同顏色繪制在圖8中，用于齒輪圖像的缺陷特征分析。

從圖8可知，多重分形譜線頂點(奇異譜f(α)為最大值的點)的右側，正常齒輪圖像多重分形譜線與缺陷齒輪圖像的多重分形譜線相互雜糅，區分困難。而在譜線頂點的左側，正常齒輪圖像與缺陷齒輪圖像的多重分形譜線相互錯開，各自成束，缺陷特征明顯，易于區分。故選擇多重分形譜線頂點左側區域的數據作為齒輪缺陷特征數據資源，如圖9所示，圖中每條譜線分別代表其對應的齒輪零件圖像的特征數據。

圖8 齒輪圖像多重分形譜

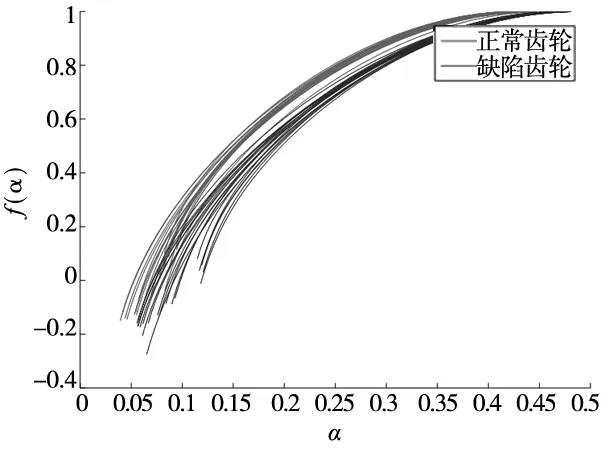
圖9 齒輪缺陷特征數據資源

2.3 齒輪圖像多重分形譜缺陷特征值提取

齒輪缺陷特征數據資源來自20張正常齒輪圖像與20張缺陷齒輪圖像，每張圖像包含106個數據，即每張齒輪圖像包含106個特征值，特征值維數為106。核主成分分析(KPCA)作為主成分分析(PCA)的一種非線性擴展方法[10]，KPCA是在PCA的基礎上利用非線性映射函數完成非線性變換，將非線性的原始低維空間數據映射到高維線性特征空間中，在線性特征空間中利用PCA算法對數據進行特征提取，從而有效地提取樣本數據的非線性信息[11]。故本文選用核主成分分析(KPCA)算法對這些數據進行降維處理，獲得精確的齒輪圖像缺陷特征值。

KPCA算法具體降維步驟如下所示：

(1)選取樣本個數為n，影響因子為m，構成的樣本數據集為A：

(2)選用核函數，目前常用的核函數主要有多項式核函數、神經網絡核函數以及高斯徑向基(RBF)核函數[12]。其中徑向核函數計算過程較簡便且分類效果好，其表達式：

(9)

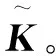
(10)

其中，

(5)選擇較大特征值的主成分，即選取前q個λi的累計貢獻率Bq需大于值0.95，如式(11)所示：

(11)

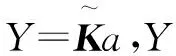
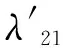
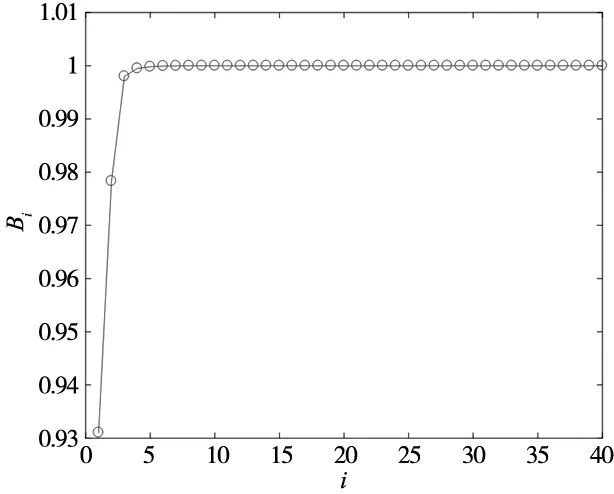
圖10 A特征值的累計貢獻率Bi

將每張正常與缺陷齒輪圖像的特征值作為二維空間點的位置坐標，如圖11所示。觀察此圖可知，齒輪缺陷數據點組成了兩個群簇分別代表正常和缺陷齒輪零件圖像，表明齒輪缺陷特征提取成功。

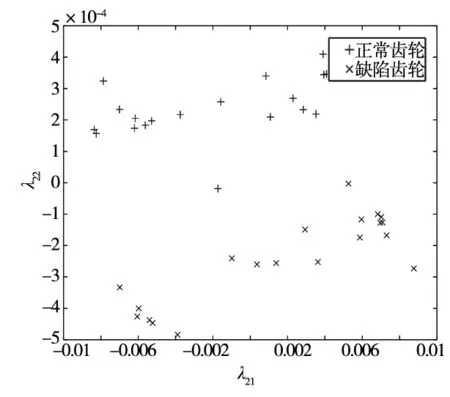
圖11 齒輪圖像缺陷特征值

3 基于MF-DFA和Lib-SVM的齒輪缺陷識別

3.1 齒輪圖像缺陷識別數據準備

(1)獲取齒輪圖像缺陷識別訓練集與測試集

成功提取齒輪圖像的缺陷特征值Y，Y為40×2的矩陣，由20張正常齒輪圖像和20張缺陷齒輪圖像組成，矩陣Y的每行數據代表每張齒輪圖像的缺陷特征值。將Y轉化為齒輪圖像缺陷識別的訓練集與測試集，根據Lib-SVM的標準[13]進行格式調整。

隨機抽取Y中10張正常和10張缺陷齒輪圖像的缺陷特征值，將其整合后作為齒輪缺陷訓練數據集D2。整合剩余的10張正常與10張缺陷齒輪圖像的特征值作為齒輪圖像缺陷測試數據集E2。D2與E2均是大小為20×2的矩陣。根據Lib-SVM標準調整D2與E2的格式，對它們進行歸一化處理得到齒輪圖像的缺陷標準訓練集train_chq2和測試集test_chq2。train_chq2與test_chq2皆是大小為20×2的矩陣。D2、E2、train_chq2及test_chq2的數據量較大，本文將每張齒輪圖像的缺陷特征值作為每個二維空間點的位置坐標，如圖12和圖13所示，即D2、E2、train_chq2及test_chq2用二維圖像進行表達。

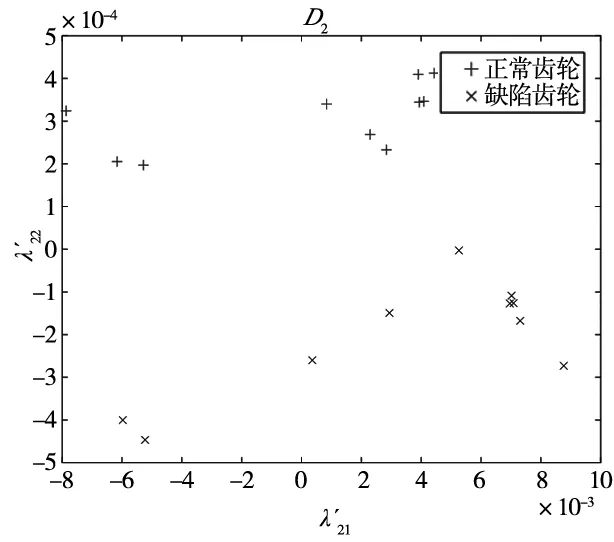
(a) 齒輪圖像缺陷訓練數據集D2

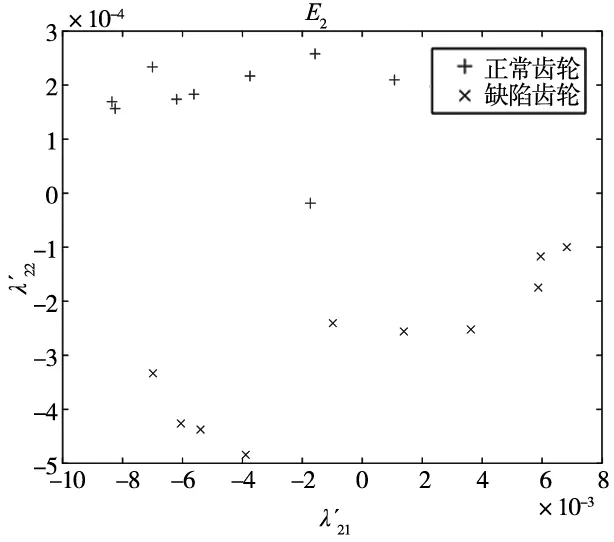
(b) 齒輪圖像缺陷測試數據集E2圖12 齒輪圖像缺陷訓練與測試數據集

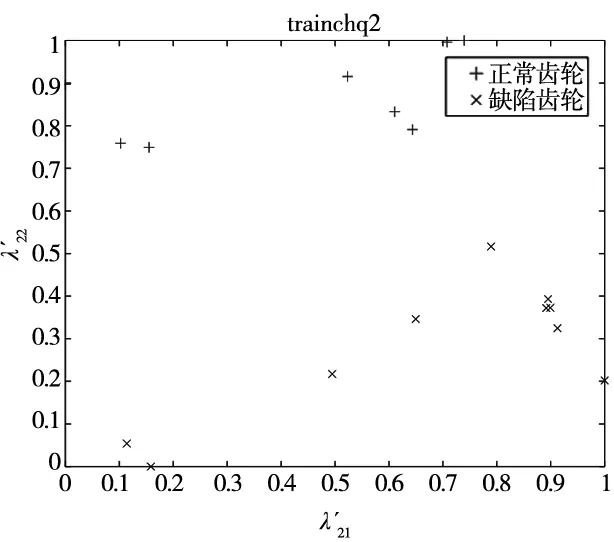
(a) 齒輪圖像缺陷標準訓練集train_chq2

(b) 齒輪圖像缺陷標準測試集test_chq2圖13 齒輪圖像缺陷標準訓練集與測試集

(2)齒輪圖像缺陷識別Lib-SVM最佳參數選擇

得到齒輪圖像的缺陷標準訓練集train_chq2后，需要將其進行交叉驗證以獲取Lib-SVM齒輪圖像缺陷識別的最佳懲罰因子c2和核函數參數g2。

在范圍2-7～27內多次改變(c2,g2)的數值，將train_chq2中20張圖像的數據隨機分成4個數據量相同的部分，依次將train_chq2的每一個部分作為齒輪測試集進行預測，train_chq2其他3個部分作為齒輪圖像訓練集對Lib-SVM進行訓練，分別計算這四個部分齒輪缺陷識別準確率的平均數p，取使p值最大時其對應的懲罰因子c2和核函數參數g2作為齒輪缺陷識別的最佳參數。

交叉驗證結果如圖14所示，圖中的線條為p等高線，每條線上的數值為p的100倍。本次測試p的最大值為100%。且有多組的數值不同的(c2,g2)參數組合可以使得p取得最大值。當懲罰參數c2過高時會造成過學習狀態，因此選取其中懲罰參數c2最小的那組作為最佳參數值，故本次最佳參數(c2,g2)的取值分別為c2=0.007 812 5，g2=0.007 812 5。

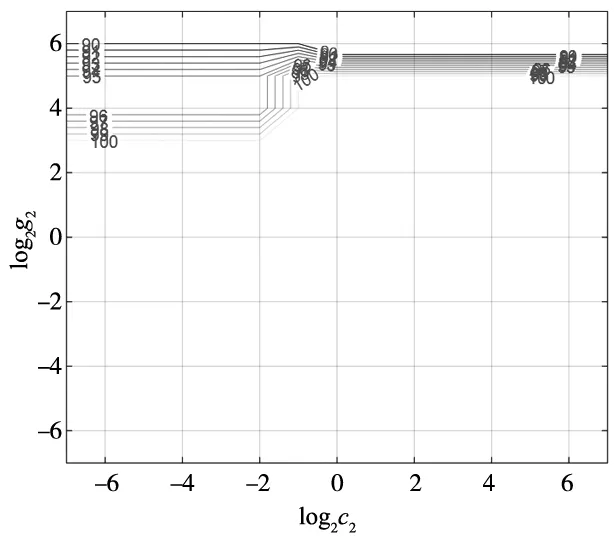
圖14 最佳參數(c2,g2)交叉驗證結果

3.2 齒輪缺陷識別預測結果與數據分析

(1)齒輪缺陷識別預測結果

將齒輪圖像最佳缺陷識別參數(c2,g2)與訓練集train_chq2帶入Lib-SVM中的樣本訓練函數(svmtrain)進行訓練可獲得齒輪圖像缺陷識別SVM模型model。隨后將model和測試集test_chq2帶入Lib-SVM中的模型測試函數(svmpredict)進行分類運算即可獲得齒輪圖像缺陷識別預測結果。本次齒輪圖像缺陷識別預測準確率Accuracy1為100%，標志著本次齒輪圖像缺陷識別成功。

如圖15所示，測試集test_chq2中20張正常與缺陷齒輪圖像的特征值全部被精準識別預測，用不同形狀和不同顏色的幾何圖形標示。其中上部區域代表正常齒輪圖像特征值預測結果，下部區域代表缺陷齒輪圖像特征值預測結果。

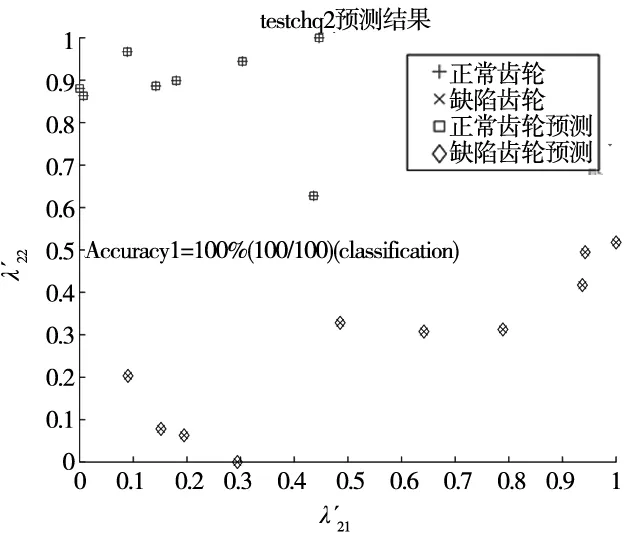
圖15 齒輪圖像缺陷識別預測結果

(2)齒輪缺陷識別結果分析

本次研究的齒輪圖像缺陷識別預測結果準確率高達100%，結果分析如下：一方面根據齒輪圖像缺陷特征數據資源，正常齒輪圖像與缺陷齒輪圖像的多重分形譜線各自聚集成束，大致錯開且無重疊現象，譜線的缺陷特征明顯。驗證了本文提出的基于三角覆蓋二維MF-DFA法計算的多重分形譜可以很好地表達零件圖像的缺陷特征。根據齒輪圖像缺陷特征值數據，進一步得到正常與缺陷齒輪圖像的數據點各自聚集成簇，同時證明本次選用KPCA可以精確提取零件圖像的缺陷特征值，再利用Lib-SVM算法建立零件圖像缺陷識別模型，能夠對零件的缺陷狀態進行精準識別預測。

4 總結

本文將常用的多重分形去趨勢波動進行改進，提出了一種基于三角覆蓋的二維MF-DFA算法，用來表達齒輪圖像的缺陷特征。使用KPCA法融合多重分形和核主成分分析，提取齒輪圖像的多重分形缺陷特征值，再采用Lib-SVM對齒輪圖像數據進行建模和缺陷識別，識別準確率高達100%。結果表明運用該方法可以很好地識別零件圖像的缺陷，標志著零件圖像缺陷識別成功，同時驗證了三角覆蓋二維MF-DFA法能夠較好地表達零件的缺陷特征。