高液靜壓無心磨床磨削過程再生顫振的穩定性分析*

徐 磊，趙麗梅，余 炯

(貴州大學機械工程學院，貴陽 550025)

0 引言

隨著工業的發展，原有的零件加工方式因加工精度不高和效率低下，已無法滿足工業的需求，無心磨削方式的出現為工業零件的高精度和高效率生產提供了解決方案，目前，無心磨床已經廣泛應用于航空航天、汽車、冶金、電力等領域圓柱形、無中心孔的短軸和圓錐體等零件的生產[1]。我國對無心磨床的研究起步較晚，近年來，為突破國外的技術封鎖，縮小與國外在無心磨削領域的差距，國內研究人員在無心磨床的自主研發方面做了大量的研究工作，但在磨削精度和效率方面與國外的無心磨床相比仍然存在較大的差距。其中造成磨床加工精度低下的主要原因在于砂輪磨削工件時發生顫振[2]。因此，從無心磨床磨削過程再生顫振機理出發，分析無心磨削的穩定性，來提高無心磨床磨削穩定性，從而提高加工精度是很有必要的[3]。

縱觀國內外對機床切削顫振的研究，有很多研究人員做了很多卓有成效的工作。文獻[4]研究了單自由度再生顫振模型，通過磨削力表達式的推導，結合振動方程分析磨削穩定性，并引入了同時考慮工件及砂輪再生顫振的雙再生效應理論。文獻[5]通過建立的切入磨再生顫振動力學模型，利用工件表面波紋度幅值的增長率為穩定性判據，研究再生顫振對磨削工件系統穩定性的影響。文獻[6]在分析外圓磨削過程的顫振增長機理的基礎上，提出了再生顫振原理的外圓磨削動力學建模方法，來研究外圓磨削的穩定性。文獻[7]推導了機床再生型切削顫振系統極限切削寬度隨主軸轉速變化的計算公式，提出了機床切削系統穩定性極限預測方法。文獻[8]以外圓磨床磨削過程為研究對象，提出了一種用于雙再生外圓磨削過程穩定性分析的系統方法，能夠直接從頻譜中獲取參數空間的穩定特性，而不需要使用時域響應。以上研究均取得了一定的研究成果，但在對機床顫振的研究中，主要是對車床、銑床和普通外圓磨床的研究，對無心外圓磨床的研究則涉及較少，而且，在建立顫振模型時，沒有考慮砂輪在磨削工件時產生的摩擦力，同時忽視了再生的磨削力和摩擦力對工件表面成形的影響，因此得出的結論具有很大的局限性，還無法指導實際生產。

本文以高液靜壓無心磨床無心磨削系統為研究對象，在分析高液靜壓無心磨床結構工作原理和實際加工的基礎上，來研究無心磨削的顫振機理；抓住高液靜壓無心磨床磨削過程的特殊性，設定了特殊的坐標系，建立了同時考慮砂輪和工件的再生和摩擦效應的無心磨削再生顫振數學模型，并計算穩定性分析的特征值，結合數值延拓算法得到穩定性葉瓣圖，為選擇合適的加工工藝參數來避免顫振提供理論依據。

1 高液靜壓無心磨床結構原理分析及磨削過程再生顫振機理研究

1.1 無心磨床的結構原理分析

高液靜壓無心磨床的工作原理分析對其工作過程的顫振機理研究和穩定性分析具有至關重要的作用，因此，對高液靜壓無心磨床進行結構分析和工作原理分析是十分必要的。本文以貴州省某廠生產的HFC-1808型高液靜壓無心磨床為研究對象，磨床的裝配結構圖如圖1所示。高液靜壓無心磨床由磨削工件的砂輪，支承并帶動工件旋轉的導輪，支承工件的托板，對砂輪的尺寸、形狀、幾何角度進行修整的砂輪修整器，對導輪的形狀、尺寸和幾何角度等進行修整的導輪修整器，滑臺，導軌，機座等組成[9]。待加工的工件放在砂輪、導輪和托板之間，由托板和導輪進行支承，在導輪的帶動下旋轉，并通過砂輪對工件進行磨削；砂輪固定在機座上，導輪和托板安裝在滑臺上，滑臺由導軌支承，通過滑臺在導軌上的移動來實現工件的進給，進而達到加工精度，很明顯，高液靜壓無心磨床的磨削方式為切入式進給磨削。

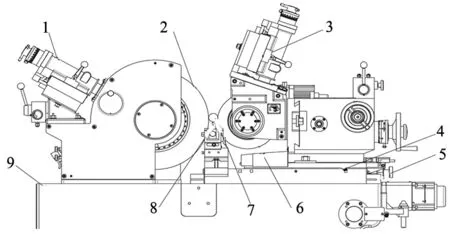
1.砂輪修整器 2.砂輪 3.導輪修整器 4.滑臺5.導軌 6.導輪 7.工件 8.托板 9.機座圖1 高液靜壓無心磨床裝配結構圖

1.2 無心磨削過程的再生顫振機理研究

在高液靜壓無心磨床切入式無心磨削過程當中，磨削輪用磨粒切割并再生工件表面，導輪帶動工件旋轉，并推動工件實現徑向進給，變相的使固定不動的砂輪完成徑向和圓周方向的進給。當工件被砂輪連續摩擦時，工件與砂輪之間產生的磨削力相互推離。根據再生顫振理論可知，磨削力和瞬時磨削深度之間存在著正比的關系[10]。磨削深度的任何變動都會引起磨削力的變化，因此時變的磨削力會激發砂輪與工件的振動，砂輪和工件的位移會影響磨削深度和磨削力，只要系統阻尼不足，這個狀態就會保持，這種自激振動稱為再生顫振。因此，為了更好了解再生效應的磨削動力學，提出了一種基于再生理論的動力學數學模型。由于托板的表面是由耐磨損材料制作而成，故在高液靜壓無心磨床磨削過程當中，托板的磨損很小，對工件的再生效應可以忽略不計。另外，導輪是調整輪，控制工件的運動，沒有參與工件的磨削，因此，對工件再生表面的影響忽略不計。

2 高液靜壓無心磨床磨削過程再生顫振動力學模型

2.1 無心磨削過程的數學模型

高液靜壓無心磨床磨削示意圖如圖2所示，Rg為砂輪的直徑，m；Mg為質量，kg；Cg為阻尼系數，N/(m/s)；Kg為剛度，N/m；ωg為磨削工件的旋轉速度，rad/s；Rw為工件的直徑，m；Mw為質量，kg；Cw為阻尼系數，N/(m/s)；Kw為剛度，N/m；ωw為旋轉速度，rad/s；工件在導輪和托板的推動下，以進給速度f(m/rev)向砂輪進給。以砂輪的回轉中心為原點，砂輪和工件的公法線方向為X軸，垂直于公法線方向為Y軸建立坐標系。基于所建立的坐標系，砂輪磨削工件的動力學控制方程可以離散為：

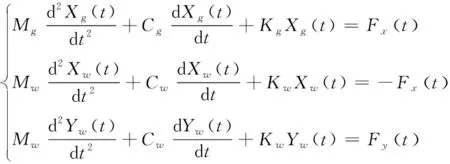
(1)

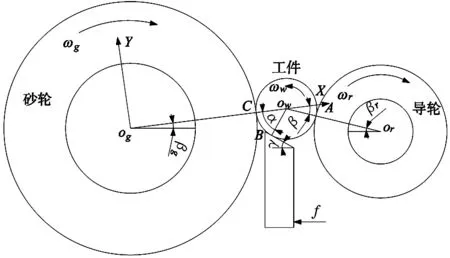
圖2 高液靜壓無心磨床磨削示意圖

2.2 切入式無心磨削磨削力

在高液靜壓無心磨床磨削工件的過程當中，給磨削系統帶來不穩定的最主要的原因主要是砂輪和工件之間的磨削力，結合外圓磨床磨削力理論，提出了一種針對于切入式無心磨床砂輪磨削工件的磨削力模型；磨削力可以分解為垂直工件徑向的切向力Ft、沿工件徑向的徑向力Fn和沿工件軸向的軸向力Fa，其中軸向力最小，可以忽略不計，切向磨削力對砂輪的影響較小，為簡化問題，在砂輪的動力學模型中，將切向磨削力忽略，只考慮徑向磨削力對砂輪的影響，結合式(1)可知，Fx和Fy分別表示工件在X方向和Y方向的激振力，并分別等于工件的徑向磨削力Fn和切向磨削力Ft。

Fx=Fn
Fy=Ft

(2)

結合高液靜壓無心磨床的工作原理可知，該無心磨床是利用砂輪磨削工件，而砂輪作為磨料磨削工具，由其上的結合劑固定的小顆粒磨料來研磨工件，從而產生時變的磨削力[11]。砂輪磨削工件表現出的外在的磨削力，實際上是由無數個單個磨粒磨削工件產生的切削力和滑擦力的合力，據此提出了圖3所示的單個磨粒磨削工件產生切削力和摩擦力的示意圖，由圖可知，在高液靜壓無心磨床磨削工件的過程中，砂輪的每個磨粒對工件表面進行切削和摩擦，并產生切向和法向的切削力和摩擦力[10]。

fct=ψfcn
fft=μffn

(3)

式(3)中，fct和fcn分別表示切削力在切向和徑向的分量，fft和ffn分別表示滑擦力在切向和徑向的分量，μ是摩擦系數，ψ是一種取決于磨粒平均尖端角的無量綱比。

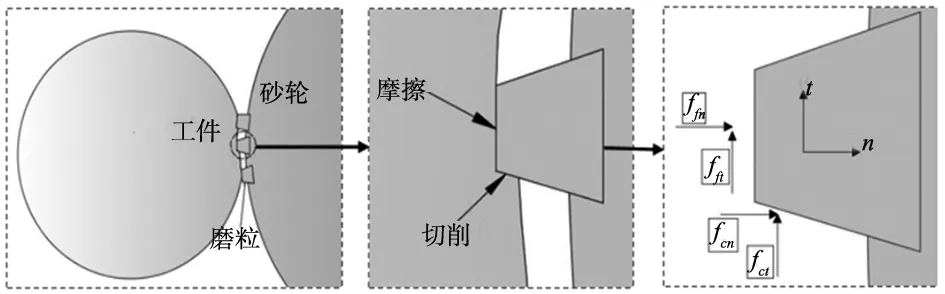
(a) 砂輪磨削工件示意圖 (b) 單個磨粒磨削示意圖 (c) 磨削中各力分量圖3 單個磨粒產生切削力和摩擦力示意圖

在高液靜壓無心磨床磨削工件的過程中，將所有參與磨削的磨粒算在內計算磨削力，得到總的徑向和切向磨削力如式(2)所示[13]：

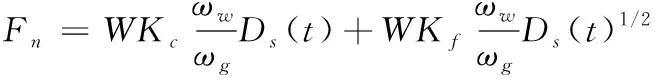
(4)

其中，Kc是切削過程系數，N/m2；Kf是滑擦過程系數，N/m3/2；W為工件的寬度；Ds(t)為取決于磨削進給和砂輪-工件相對位移的瞬時磨削深度。

根據再生理論來確定磨削深度Ds(t)，同時考慮工件進給和工件與砂輪的相對位移，則磨削深度為：

Ds(t)=fcos(βg)+Xw(t)-Xg(t)-εYw(t)
(0<ε<1)

(5)

磨削是一個工件材料連續被砂輪移除生成新表面的過程，因此，在先前(t-Tw)時工件和砂輪相對位移的任何變動，都會影響瞬時磨削深度Ds(t)，則磨削深度Ds(t)變為：

Ds(t)=fcos(βg)+(Xw(t)-Xg(t)-εYw(t))-

Xw(t-Tw)-Xg(t-Tw)-εYw(t-Tw)

(6)

而且，在磨削過程中，砂輪是不斷磨損生成新表面的過程，因此，在雙再生效應的影響下，磨削深度Ds(t)變成：

Ds(t)=fcos(βg)+(Xw(t)-Xg(t)-εYw(t))-

Xw(t-Tw)-Xg(t-Tw)-εYw(t-Tw)-

g(Xw(t-Tg)-Xg(t-Tg)-εYw(t-Tg))

(7)

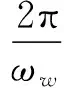
除了再生效應，利用一個符號函數來考慮滑擦，則式(4)中砂輪和工件之間的摩擦系數μ是切向相對速度Vf的函數。

μ=sign(Vf)μd

(8)

如圖4所示，砂輪和工件之間的切向相對速度Vf取決于砂輪和工件的旋轉，二者的平面運動，即：

Vf=Vfg-Vfw

(9)

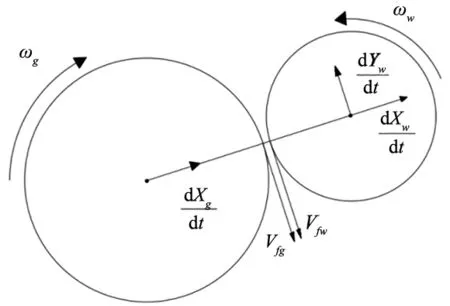
圖4 砂輪和工件在接觸區切向相對速度示意圖

式中，Vfg和Vfw分別是砂輪和工件在接觸區的切向速度：

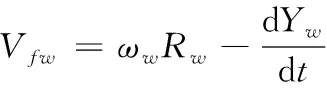
(10)

3 高液靜壓無心磨床磨削過程穩定性分析

在1965年，自Tobias首次提出穩定性葉瓣圖的概念開始[14]，穩定性葉瓣圖逐步發展并作為一種在切削加工規劃階段用來預測切削穩定性和用來解釋機床動態切削過程行為的一種方法，并被大家廣泛接受。但是，在穩定性葉瓣圖的構建當中，人們只熱衷于車床或銑床切削過程穩定性葉瓣圖的構建，對切入式無心磨床磨削過程穩定性葉瓣圖的構建，幾乎沒有涉獵。因此本節嘗試從構建切入式無心磨床磨削過程穩定性葉瓣圖的角度出發，來研究高液靜壓無心磨床磨削過程穩定性。

在高液靜壓無心磨床穩定磨削的過程中，令X(t)=[xg(t)xw(t)yw(t)]T，將式(4)、式(8)～式(10)代入式(1)，可以得到如下磨削模型:

(11)

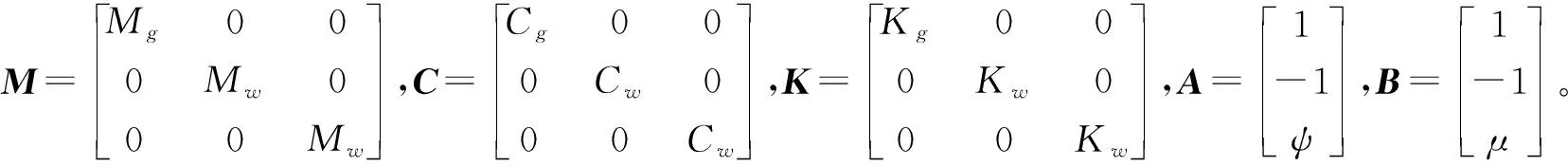
本文以MK1808型高液靜壓無心磨床為研究對象，將要用于計算和分析的參數值列于表1。

表1 穩定性仿真參數值

通過MATLAB編程對式(11)來進行特征值計算并結合數值延拓算法得到HFC-1808型高液靜壓切入磨無心磨床的穩定性葉瓣圖(如圖5所示)，該圖以砂輪轉速為橫坐標，工件的徑向磨削深度為縱坐標。

圖5 高液靜壓無心磨床磨削穩定性葉瓣圖

圖5所示的砂輪再生顫振穩定性葉瓣圖，由不同的臨界點連接而成，并將整個平面分成兩個區域，每個區域具有不同的穩定性性質，依據穩定性性質的不同可分成4個穩定性區域。

(1)切入式無心磨削顫振區：當砂輪轉速和徑向磨削深度匹配點完全位于曲線上方時，如圖中的G1點，砂輪要發生再生顫振，這時無論怎樣選擇砂輪轉速和磨削深度，砂輪磨削工件都會發生顫振，從而引發一系列的危害，因此，切入式無心磨削顫振區應堅決避免。

(2)切入式無心磨削臨界穩定區：當砂輪轉速和徑向磨削深度匹配點剛好落在曲線上時，如圖中G2點，為切入式無心磨削臨界穩定區，此時，砂輪磨削工件可能會發生顫振，也可能穩定的磨削，總之，只要顫振發生，就會嚴重影響工件的磨削精度，因此，切入式無心磨削臨界穩定區也是應該避免的區域。

(3)切入式無心磨削有條件穩定區：當砂輪轉速和徑向磨削深度匹配點落在極限磨削點劃線hlim和葉瓣圖曲線之間時，如圖中G3點，為切入式無心磨削有條件穩定區；當砂輪轉速固定不變，隨著徑向磨削深度的增加，匹配點先后經過穩定區和顫振區，砂輪先穩定后發生顫振；當固定徑向磨削深度，隨著砂輪轉速的增加，穩定區和顫振區相間出現。

(4)切入式無心磨削無條件穩定區：當砂輪轉速和徑向磨削深度匹配點落在極限磨削點劃線以下時，如圖中G4點，為切入式無心磨削無條件穩定區，在此區域，無論如何選擇砂輪轉速和徑向磨削深度，砂輪都不會發生顫振。

綜上所述，結合高液靜壓無心磨床穩定性葉瓣圖，可以選取適當工藝參數，從而避免砂輪磨削工件時顫振的發生(顫振狀態即為不穩定狀態)，從而達到提高加工精度和生產效率的目的。并且，高液靜壓無心磨床磨削穩定性葉瓣圖為企業在生產加工時的參數選擇提供了依據，同時，也為相關磨床的穩定性分析提供了新的思路。

4 結論

(1)應用再生顫振理論，得出高液靜壓無心磨床磨削工件時的不穩定原因主要是因為砂輪和工件發生了再生顫振引起的。

(2)以再生顫振機理為基礎，建立了同時考慮砂輪和工件再生顫振的動力學模型。

(3)求解動力學模型矩陣方程，利用MATLAB編程得到高液靜壓無心磨床切入式無心磨削穩定性葉瓣圖，并根據砂輪轉速和徑向磨削深度匹配點的不同，將穩定性葉瓣圖劃分為4個區域，為磨削工藝參數的選擇提供了理論依據。