基于DXF的復雜工件標定及相機參數優化

于躍華，王好臣，趙錦澤，叢志文，高茂源，李家鵬

(山東理工大學機械工程學院，山東 淄博 255000)

0 引言

目前具有視覺識別的機械臂末端定位技術早已成為機器視覺研究的熱點問題，基于視覺識別伺服的機器人逐漸被應用到各種行業中，比如焊接機器人、工件分揀機器人等，極大地提高了我國工業的生產效率與自動化程度[1-3]。在實現對工業機器人視覺引導的過程中，有效提高工件與相機內參的標定精度成為了視覺伺服在工業應用中亟待解決的關鍵問題[4]。

本文在工件標定時對易使用CAD建模的工件進行DXF文件提取，將CAD工作單元與實際工作單元中的工件進行調整與坐標轉換，為工件標定提供了圖元坐標信息，有效地減少了人工示教。針對相機標定提出了一種基于自適應權重粒子群算法的參數優化方法，該方法在傳統粒子群算法的基礎上建立了自適應權重函數，提高了全局搜索能力，避免了傳統算法優化時易陷入局部最優的問題，有效提高了標定精度。

1 復雜工件標定

標定復雜零件時，針對不同零件需采用適合的標定方法，常見的復雜工件一般為具有圓形基準面或相交平面的工件，極少出現更復雜的三維圖形，因此只針對存在圓基準面和正交平面的工件進行標定研究。

1.1 圓形基準工件四點標定法

四點標定法(圖1)用于具有圓形定位基準的工件，優點為只需要找出基準圓上任意不同三點和工件上的一個其他基準點即可。

圖1 圓弧四點標定法

基準圓的尺寸及圓心位置由其上任意三點確定，圓的位置信息則通過另一明顯基準點來確定，調整工件時先使兩基準圓重合，再將工件上的特征點對應，最后繞基準圓過圓心的法向軸線旋轉一定角度即可[9]。

設b1(Xb1，Yb1，Zb1)，b2(Xb2，Yb2，Zb2)，b3(Xb3，Yb3，Zb3)三點分別為CAD環境中基準圓上任意三點，b4(Xb4，Yb4，Zb4)為工件上任意特征點，則該基準圓的平面法矢量和圓心b0(Xb0，Yb0，Zb0)可以確定，點b1，b2，b3確定的圓平面方程可由下式表示：

Ab1(X-Xb1)+Bb1(Y-Yb1)+Cb1(Z-Zb1)=0

(1)

式中：

Ab1=(Zb3-Zb1)(Yb2-Yb1)-
(Zb2-Zb1)(Yb3-Yb1)
Bb1=(Zb2-Zb1)(Xb3-Xb1)-
(Zb3-Zb1)(Xb2-Xb1)
Cb1=(Xb2-Xb1)(Yb3-Yb1)-
(Xb3-Xb1)(Yb2-Yb1)

定義該平面的法矢量為CAD單元中工件坐標系的Zb軸矢量，可表示為：

Zb=αbzi+βbzj+γbzk

(2)

其中：

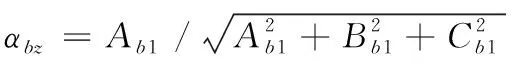
圓心b0的位置可由圓的方程得出：

(X-Xb0)2+(Y-Yb0)2+(Z-Zb0)2=R2

(3)

將b1、b2、b3三點坐標帶入式(3)，得到：

(Xb1-Xb0)2+(Yb1-Yb0)2+
(Zb1-Zb0)2=R2

(Xb2-Xb0)2+(Yb2-Yb0)2+
(Zb2-Zb0)2=R2

(Xb3-Xb0)2+(Yb3-Yb0)2+
(Zb3-Zb0)2=R2

因圓心在圓平面上，則可得到方程：

Ab1(Xb0-Xb1)+Bb1(Yb0-Yb1)+
Cb1(Zb0-Zb1)=0

(4)

將以上方程聯立求解，可得到工件坐標系Yb軸的矢量為：

Yb=Lb0→b4×Zb=αbyi+βbyj+γbyk

(5)

其中，Lb0→b4為點b0到點b4的單位化向量。根據右手法則可知Xb軸的矢量為：

Xb=Yb×Zb=αbzi+βbzj+γbzk

(6)

(7)

(8)

該方法只需保證工件中某一特征點對應，對基準圓上的任意三點沒有任何要求，可廣泛應用于具有圓形定位基準的工件。

1.2 正交平面六點標定法

圖2為正交平面工件標定算法示意圖，Ow-XwYwZw為機器人基坐標系；兩個長方體從左到右分別處于由六點確定的仿真工作單元坐標系和實際工作單元坐標系。

圖2 正交平面六點標定法

2 DXF離線編程技術

在對復雜工件進行標定時，因其本身因素會對標定精度產生影響，本文將工件DXF文件的提取與四點定位和六點定位標定方法相結合，使CAD坐標與工件的實際坐標統一，輔助了復雜工件的標定。

2.1 DXF文件的介紹

DXF(Drawing Exchange Format)文件是Autodesk公司推出的一個與外部CAD/CAM進行圖形數據交換的接口，其內容以代碼形式出現，是一種開放的矢量數據，組成部分如圖3所示。

工件標定過程中所需圖元信息包含在圖形交換格式(DXF)文件中，一般的DXF文件數據信息量巨大，提取時應對文件進行篩選[6]。而標定所需的圖形位置坐標信息只存在于實體段(ENTITIES)中，因此只對DXF文件內的實體段段進行提取即可[7]。

圖3 DXF文件格式圖

2.2 DXF數據提取流程

實體段信息的復雜程度由工件決定，為保證提取效率和識別的準確度，提取流程必須簡潔高效，能夠有條理、有選擇的對實體段的信息進行提取整理[8]。

文件提取過程如圖4所示，首先打開DXF文件對信息進行讀取，當判斷信息為實體段首行時，開始對四種圖元類型依次判斷，最后對厚度進行判斷，當檢測到文件信息為實體段尾時，關閉DXF，提取結束，最終可以得到機器人需要的參數信息。

圖4 DXF數據提取流程圖

2.3 DXF提取程序設計

常見的復雜工件中的圖形信息基本都由直線和圓弧組成，所以程序的設計主要針對直線段與圓弧。

當用VC來設計DXF文件的讀取[9]處理ASCII碼時，需要用到C語言處理的兩個標準函數：fprintf()和fscanf()。首先使用fopen()指令打開DXF文件，按照順序讀取到文件結束，然后利用位置指針函數fprintf()，標記當前位置。如需遍歷完整文件，則按照位置順序從上往下，讀取完一個字符自動移到下一個字符的位置[10]。

下面以圓弧信息的提取為例：首先使用Str=ReadDxfFile(fp) 命令開始讀取文件，依次判斷讀取處是否為實體段和圓弧信息段，隨后確定圓心坐標X、Y、Z方向坐標值，然后判斷圓弧半徑組值、起始角度組值、終止角度組值，最后使用 If (str = "EOF") 命令判斷是否為末尾，結束讀取并退出。

提取直線段信息時將代碼中的“ARC”更改為“LINE”，并判斷直線的起始點和終止點坐標值，直線段起始點的X、Y、Z坐標組碼與圓心坐標相同，分別為10、20、30，直線段終止點的X、Y、Z坐標組碼分別為11、21、31，而圓弧的半徑、起始角度、終止角度組碼分別為40、50、51。提取后，機器人可以根據程序完成相應的動作。

以一具有圓弧和直線段的圖形為例，用VC軟件對DXF文件進行提取，后續在人機交互界面中輸出提取形成的圖形。圖5為CAD軟件中繪制的圖形，圖6為提取DXF文件生成的圖形，可見DXF文件提取的方法完全符合精度要求。

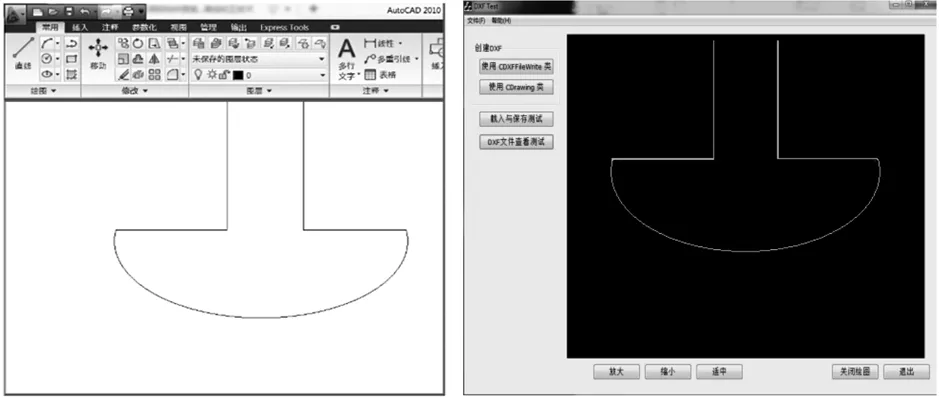
圖5 CAD中工件圖像 圖6 DXF提取圖像

3 相機標定實驗

3.1 相機成像模型

相機成像模型是一種用來描述成像平面像點與空間物點之間數學投影關系的模型[4],圖7為相機成像的幾何模型，成像關系為線性變化。

圖7 相機成像模型

視覺系統獲取圖像是一個比較復雜的過程，在描述獲取圖像與攝像頭之間的關系時，一般在視覺系統中主要使用4種坐標系，如圖所示，分別為：世界坐標系Ow-xwywzw、相機坐標系Oc-XcYcZc、圖像物理坐標系o-xy和圖像像素坐標系Op-uv。Op為相機的光心，O為成像主點。

世界坐標系中一點Pw在像素坐標系內的投影點Pp為Pw與成像平面的交點，二者的關系為：

其中，ax和ay分別為相機在x軸和y軸上的焦距，單位為mm，u0和v0為成像主點的坐標值，A為內部參數矩陣，M為外部參數矩陣。當世界坐標系中的一點投影到像素坐標系中，會發生很大變化，同時也會損失很多信息，因為鏡頭并不是理想的透視成像模型，都存在不同程度的畸變，因此必須要考慮相機畸變，所以有：

本文中考慮了鏡頭的二階徑向畸變n1、n2和切向畸變pu、pv，(xk,yk)為畸變后的坐標，(xu,yu)為畸變前的坐標。

3.2 相機內參優化

在對物體識別與定位的過程中需要對相機進行標定和參數優化。相機標定的方法有傳統標定方法、自標定方法以及主動視覺標定方法[11-12]，一般使用傳統標定方法較多，目前主要有線性標定法、Tsai兩步法[13]、張正友標定法[14]等。其中張正友標定法操作簡便可靠，對設備要求不高，被廣泛應用。但該方法使用的傳統優化算法易陷入局部最優，標定精度有待提高。相機標定作為視覺基礎已有多種成熟的標定方法，本次標定使用張正友標定法，該方法是一種介于傳統標定和相機自標定之間的標定方法。該方法對相機內參數初始值的求解已非常成熟，本文中不再贅述。大致標定過程為：選用棋盤格為標定參照物，保證相機固定，對棋盤進行不同角度的多次拍攝，將左右相機拍攝到的圖片相對應，并對線條進行測量。利用已知的棋盤格角點坐標得到對應的圖像坐標，即可求出單應矩陣。然后根據求得的單應矩陣和旋轉矩陣R推出內部參數矩陣A，進而得到理論層面的內部參數與外部參數。

張正友標定法簡單易操作、精度高、魯棒性好，經過標準計算確定了理論上的可行性。但該方法未考慮實際應用中畸變與噪聲的影響，因此需要把標定結果作為初始條件進一步優化。

假設相機在標定時采集到m張不同的棋盤格標定板圖像，每幅圖像包含p個角點，已知內部參數矩陣A、旋轉矩陣R、平移向量s。令其中一個棋盤格角點為T，經過透視、旋轉平移變換后得到一由A、R、s、T組成的函數，記t′，進而建立如下目標函數：

(9)

式中，t′為該角點的理論像素坐標，i表示圖片的順序數，j表示該圖片上的角點順序數，tij為第i幅圖像上第j個角點的實際像素坐標，Ri、si分別表示第i幅圖像的旋轉矩陣和平移向量，Tj為第j個角點的坐標。由于理論像素坐標和實際像素坐標中的誤差包含鏡頭畸變的影響，所以畸變參數應添加到目標函數得優化中，得到新的目標函數為：

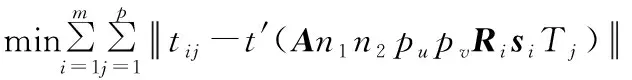
(10)

至此，問題已轉化為最小二乘法的線性優化問題，常用的傳統方法有LM法、最速下降法等。

4 基于自適應權重粒子群算法的相機參數優化

4.1 基本粒子群算法

傳統算法如LM法等在優化過程中易陷入局部最優，現提出一種改進粒子群算法，能有效避免優化過程中因算法過早收斂而陷入局部最優的問題。

粒子群算法(PSO)是進化算法的一種，從隨機解出發，迭代尋找最優，通過適應度來評價解的品質。PSO算法精度高、易實現、收斂快，對種群數量和初始速度要求不高，全局搜索能力比傳統算法更強，在解決實際問題中展現出其優越性。

PSO初始化為空間中的一群隨機粒子，位置表示為矢量Xi，速度為矢量Vi，每個粒子都有一個由目標函數確定的適應值(fitness value),它們在尋找全局最優解時不斷交流，將自己找到的最好位置(Pbest)傳遞給所有粒子，這樣每個粒子就可得到當前群體中發現的最好位置(Gbest)，并通過自己的位置和同伴中最好的位置來決定下一步的運動。粒子的條件更新方程可以用下式表示：

(11)

式中，t代表當前迭代次數；ω代表慣性權重，為非負數；c1和c2自身和社會學習因子，一般取2；r1和r2為(0,1)區間內互不干涉的隨機數。

4.2 改進粒子群算法

慣性權重ω在算法尋優時發揮著重要作用，其值較大時，算法的全局搜索能力強，局部搜索能力變弱，其值較小時相反。為避免算法過早收斂，我們令慣性權重隨著粒子適應度而發生改變，創建了一種用于相機標定的自適應權重法，假設群體中初始粒子的個數設置為n，具體函數關系如下：

當F(xi)≤Fv時，

(12)

當F(xi)>Fv時，

(13)

其中，

(14)

其中，ωmin為慣性權重最小值，ωmax為慣性權重的最大值，F(xi)為第i個粒子的位置在目標函數式(10)中的值，Fmin為該次迭代F(xi)中的最小值，Fmax為該次迭代中F(xi)的最大值。迭代過程中，當粒子所處位置比其他粒子更優時，慣性權重值變小，使該粒子有較好的局部搜索能力，更快找到更優位置。當粒子位置較差時，慣性權重值變大，使粒子快速脫離該位置，轉向全局搜索。這樣可保證粒子在運動時既能向全局最優值靠攏，又能保持一定的全局搜索能力，避免粒子群在搜索的時候陷入局部最優。

4.3 相機標定參數優化結果

對12幅不同角度和位置的標定板圖像進行采集，將角點網格進行提取并標定，得到的角點網格與相機位置關系圖如圖8所示。

圖8 相機與棋盤格角點位置關系

標定選用焦距為8 mm的定焦鏡頭，實驗用棋盤格標定板在X方向棋盤格數目為10，Y方向數目為7，單個黑白格尺寸為25 mm×25 mm。設置粒子群數目i=150，迭代次數t=400，慣性權重ωmax=0.8，ωmin=0.3，自身學習因子c1和c2=1.5，社會學習因子c2=2。

表1中為兩種方法求得的相機內部參數，根據表中各項參數值來看，自適應權重粒子群算法在精確度上優于張正友標定法。為進一步驗證兩種方法的精確程度，需要對其重投影誤差進行計算。

表1 相機內參標定結果

圖9為張正友標定法重投影誤差，圖10為自適應權重粒子群算法重投影誤差。可以看出自適應權重粒子群算法的精度更好，具有更高的可行性。

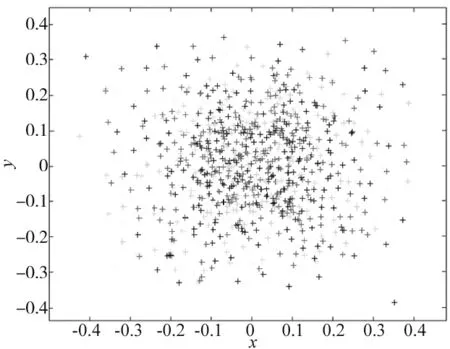
圖9 張正友標定法重投影誤差

圖10 自適應權重粒子群算法重投影誤差

5 結論

為提高基于視覺伺服的工業機器人的工作精度，針對工件標定與相機標定環節分別提出了DXF提取輔助標定和基于自適應權重粒子群算法的相機內參優化方法，通過對DXF信息進行提取，為工件的標定提供了精準的圖元坐標信息，實現了CAD單元與實際工作單元工件坐標信息的統一；建立添加了二階畸變的相機模型，并通過張正友標定法確定了內參的初始值，創建了添加畸變的目標函數，然后使用自適應權重粒子群算法對目標函數進行優化，最后在標定實驗中將該算法取得的參數和與張正友標定法中的傳統優化方法進行了對比，并且對參數進行了重投影誤差分析，結果進一步證明了自適應權重粒子群算法在相機內參優化過程中能取得更好的結果，有效的提高了標定精度，是一種可靠的方法。